Với giải Câu hỏi trang 60 Toán 10 Tập 1 Cánh Diều trong Bài tập cuối chương 3 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 60: Bài tập cuối chương 3
Bài 1 trang 60 Toán 10 tập 1: Tìm tập xác định của mỗi hàm số sau:
a)
b)
c)
Phương pháp giải:
xác định
xác định
xác định
Lời giải:
a) xác định
Tập xác định
b) xác định
Tập xác định
c) xác định
Tập xác định
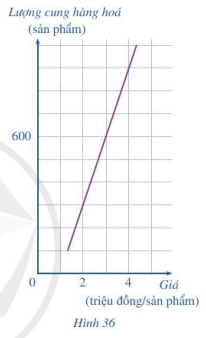
a) Xác định lượng hàng hoá được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đồng; 4 triệu đồng.
b) Biết nhu cầu thị trường đang cần là 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)?
Phương pháp giải:
a) Tìm điểm trên đồ thị có hoành độ bằng 2 và bằng 4. Từ đó tìm tung độ.
b) Tìm điểm trên đồ thị có tung độ bằng 6. Từ đó tìm hoành độ.
Lời giải:
a) Từ đồ thị ta thấy khi giá bán là 2 triệu đồng/sản phẩm thì lượng cung hàng hóa là: 300 sản phẩm, khi giá bán là 4 triệu đồng/sản phẩm thì lượng cung hàng hóa là 900 sản phẩm.
b) Khi nhu cầu thị trường là 600 sản phẩm, để cân bằng thị trường thì lượng cung bằng lượng cầu. Khi đó lượng cung hàng hóa cũng là 600 sản phẩm.
Từ đồ thị ta thấy khi lượng cung hàng hóa là 600 sản phẩm thì giá bán là 3 triệu đồng/sản phẩm.
Gói A: Giá cước 190 000 đồng/tháng.
Nếu trả tiền cước ngày 6 tháng thì sẽ được tặng thêm 1 tháng.
Nếu trả tiền cước ngày 12 tháng thì sẽ được tặng thêm 2 tháng.
Gói B: Giá cước 189 000 đồng/tháng.
Nếu trả tiền cước ngày 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng.
Nếu trả tiền cước ngày 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng.
Giả sử số tháng sử dụng Internet là x (1 nguyên dương).
a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian
dùng không quá 15 tháng.
b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào?
Phương pháp giải:
a) Lập hàm số thể hiện số tiền phải trả theo từng loại gói riêng biệt.
b)
Lời giải:
a)
Gói A:
Hàm số:
Gói B:
Hàm số:
b)
Gia đình bạn Minh dùng 15 tháng,
+) Nếu chọn gói A: Số tiền phải trả là (đồng)
+) Nếu chọn gói B: Số tiền phải trả là 2268000 đồng.
Vậy gia đình bạn Minh nên chọn gói B.
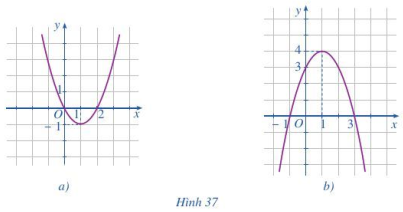
Quan sát đồ thị hàm số bậc hai ở Hình 37a và Hình 37b rồi nêu:
a) Dấu của hệ số a;
b) Toạ độ đỉnh và trục đối xứng;
c) Khoảng đồng biến;
d) Khoảng nghịch biến;
e) Khoảng giá trị x mà y > 0;
g) Khoảng giá trị x mà .
Phương pháp giải:
a) Xác định bề lõm và so sánh a với 0
b) Xác định đỉnh và trục đối xứng của mỗi đồ thị.
c) Quan sát đồ thị và tìm khoảng đồng biến
d) Quan sát đồ thị và tìm khoảng nghịch biến
e) Khoảng giá trị x mà đồ thị nằm trên trục Ox
g) Khoảng giá trị x mà đồ thị nằm dưới trục Ox
Lời giải:
a)
Hình 37a: Bề lõm hướng lên trên nên a>0
Hình 37b: Bề lõm xuống nên a<0
b)
Hình 37a: Đỉnh là (1;-1), trục đối xứng x=1
Hình 37b: Đỉnh là (1;4), trục đối xứng x=1
c)
Hình 37a: Hàm số đồng biến trên
Hình 37b: Hàm số đồng biến trên
d)
Hình 37a: Hàm số nghịch biến trên
Hình 37b: Hàm số nghịch biến trên
e)
Hình 37a: Đồ thị nằm trên trục Ox khi
=> Khoảng giá trị x mà y > 0 là
Hình 37b: Đồ thị nằm trên trục Ox khi
=> Khoảng giá trị x mà y > 0 là
g)
Hình 37a: Đồ thị nằm dưới trục Ox khi
=> Khoảng giá trị x mà y < 0 là
Hình 37b: Đồ thị nằm dưới trục Ox khi
=> Khoảng giá trị x mà là
Xem thêm lời giải SGK Toán 10 Cánh Diều hay, chi tiết khác:
Bài 1 trang 60 Toán 10 tập 1: Tìm tập xác định của mỗi hàm số sau,...
Bài 5 trang 61 Toán 10 tập 1: Vẽ đồ thị của mỗi hàm số sau...
Bài 6 trang 61 Toán 10 tập 1: Lập bảng xét dấu của mỗi tam thức bậc hai sau...
Bài 7 trang 61 Toán 10 tập 1: Giải các bất phương trình sau...
Bài 8 trang 61 Toán 10 tập 1: Giải các phương trình sau...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.