Với giải Câu hỏi trang 61 Toán 10 Tập 1 Cánh Diều trong Bài tập cuối chương 3 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 61: Bài tập cuối chương 3
Bài 5 trang 61 Toán 10 tập 1: Vẽ đồ thị của mỗi hàm số sau:
a)
b)
c)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục .
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số .
Lời giải:
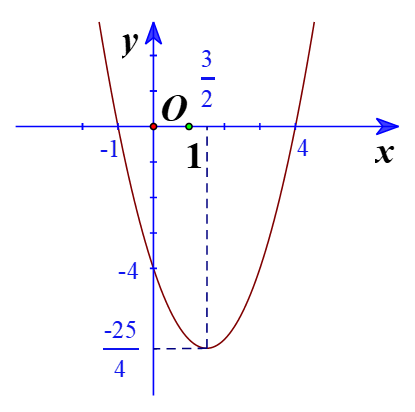
a)
Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;-4)
Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
Điểm đối xứng với điểm (0;-4) qua trục đối xứng là (3;-4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
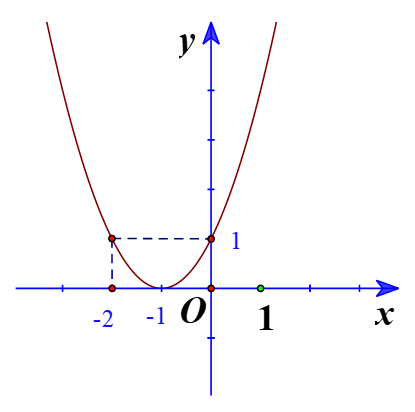
b)
Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
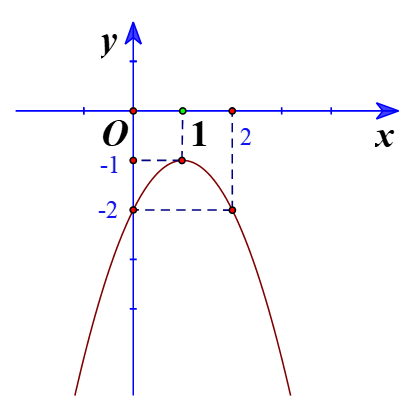
c)
Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;-2)
Điểm đối xứng với điểm (0;-2) qua trục đối xứng là (2;-2)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
Bài 6 trang 61 Toán 10 tập 1: Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a)
b)
c)
Phương pháp giải:
Bước 1: Tìm nghiệm của và hệ số a.
Bước 2: Lập bảng xét dấu.
Lời giải:
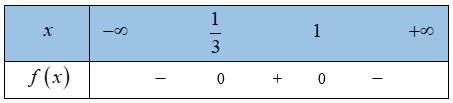
a)
,
=> có 2 nghiệm
Bảng xét dấu:
b)
,
=> có 2 nghiệm
Bảng xét dấu:

c)
,
=> có nghiệm duy nhất
Bảng xét dấu:
Bài 7 trang 61 Toán 10 tập 1: Giải các bất phương trình sau:
a)
b)
c)
d)
e)
g)
Phương pháp giải:
Giải bất phương trình dạng .
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của (nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng được giải bằng cách tương tự.
Lời giải:
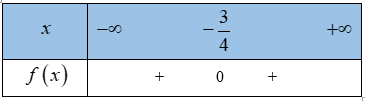
a)
Tam thức bậc hai có 2 nghiệm phân biệt
hệ số
Ta có bảng xét dấu f(x) như sau:
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
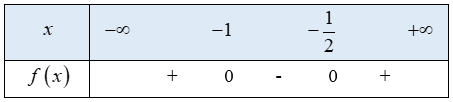
b)
Tam thức bậc hai có 2 nghiệm phân biệt
Hệ số
Ta có bảng xét dấu f(x) như sau:
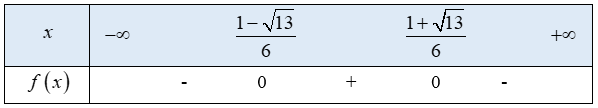
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
c)
Tam thức bậc hai có nghiệm duy nhất
hệ số
Ta có bảng xét dấu f(x) như sau:
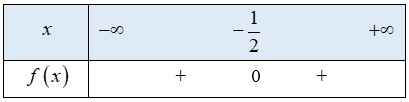
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
d)
Tam thức bậc hai có nghiệm duy nhất
hệ số
Ta có bảng xét dấu f(x) như sau:
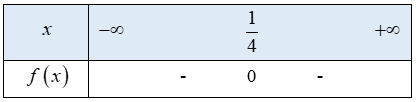
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
e)
Ta có và có
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “-” là
Vậy tập nghiệm của bất phương trình là
g)
Tam thức bậc hai có và có
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “-” là
Vậy tập nghiệm của bất phương trình là
Bài 8 trang 61 Toán 10 tập 1: Giải các phương trình sau:
a)
b)
c)
Phương pháp giải:
Phương trình dạng
Bước 1: Bình phương hai vế và đưa về phương trình bậc hai một ẩn.
Bước 2: Thay các giá trị tìm được vào bất phương trình . Nghiệm nào thỏa mãn thì giữ lại, không thỏa mãn thì loại.
Bước 3: Kết luận nghiệm
Phương trình có dạng
Bước 1. Giải bất phương trình để tìm tập nghiệm của bất phương trình đó.
Bước 2. Bình phương hai vế của phương trình rồi tìm tập nghiệm.
Bước 3. Trong những nghiệm của phương trình ở bước 2, ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình . Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình đã cho.
Lời giải:
a)
Điều kiện:
Bình phương 2 vế của phương trình ta được:
b)
Bình phương 2 vế của phương trình ta được:
Thay vào bất phương trình ta thấy cả 2 nghiệm đều thỏa mãn.
Vậy tập nghiệm là
c)
Điều kiện:
Bình phương 2 vế của phương trình ta được:
Vậy tập nghiệm là
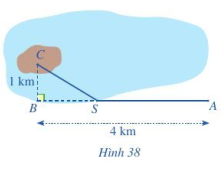
Lời giải:
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
(km)
(km)
Tổng số tiền từ A đến C là:
(triệu đồng)
Khi đó ta có phương trình:
Do
=>
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)
Xem thêm lời giải SGK Toán 10 Cánh Diều hay, chi tiết khác:
Bài 1 trang 60 Toán 10 tập 1: Tìm tập xác định của mỗi hàm số sau,...
Bài 5 trang 61 Toán 10 tập 1: Vẽ đồ thị của mỗi hàm số sau...
Bài 6 trang 61 Toán 10 tập 1: Lập bảng xét dấu của mỗi tam thức bậc hai sau...
Bài 7 trang 61 Toán 10 tập 1: Giải các bất phương trình sau...
Bài 8 trang 61 Toán 10 tập 1: Giải các phương trình sau...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.