Với giải Câu hỏi trang 75 Toán 10 Tập 2 Cánh Diều trong Bài 3: Phương trình đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 75 Bài 3: Phương trình đường thẳng
Luyện tập 1 trang 75 Toán lớp 10 Tập 2: Cho đường thẳng Δ có phương trình tham số
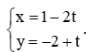
a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng Δ.
b) Điểm nào trong các điểm C(– 1; – 1), D(1; 3) thuộc đường thẳng Δ.
Lời giải:
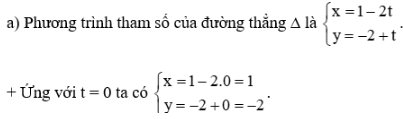
Điểm A(1; – 2) thuộc đường thẳng ∆.
+ Ứng với t = 1 ta có
Điểm B(– 1; – 1) thuộc đường thẳng ∆.
Chú ý: Ta chỉ cần lấy một số thực t bất kì thay vào phương trình tham số, ta sẽ được tọa độ 1 điểm thuộc đường thẳng ∆.
b) Theo câu a) điểm B(– 1; – 1) thuộc đường thẳng Δ ứng với t = 1, khi đó C ≡ B.
Vậy điểm C(– 1; – 1) thuộc đường thẳng ∆.
Thay tọa độ điểm D(1; 3) vào đường thẳng Δ ta được:
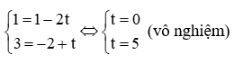
Vậy điểm D(1; 3) không thuộc đường thẳng ∆.
Hoạt động 3 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ có giá vuông góc với đường thẳng ∆ (Hình 27).
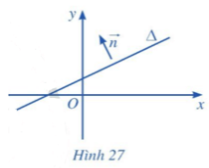
Lời giải:
Cách vẽ:
- vẽ 1 đoạn thẳng vuông góc với đường thẳng ∆.
- Vẽ hướng mũi tên trên đoạn thẳng đó, ta được vectơ chỉ phương thỏa mãn yêu cầu bài toán.
Hoạt động 4 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và có vectơ pháp tuyến . Xét điểm M(x; y) nằm trên ∆ (Hình 28)
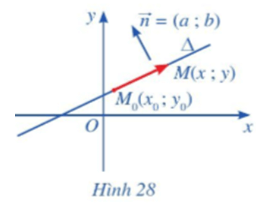
a) Nhận xét về phương của hai vectơ và .
b) Tìm mối liên hệ giữa tọa độ của điểm M với tọa độ của điểm M0 và tọa độ của vectơ pháp tuyến .
Lời giải:
a) Vectơ là vectơ pháp tuyến của đường thẳng ∆ nên giá của vectơ vuông góc với đường thẳng ∆.
Đường thẳng ∆ đi qua điểm M0 và M, nên đường thẳng ∆ chính là đường thẳng MM0. Khi đó vectơ có giá chính là đường thẳng ∆.
Do đó giá của vectơ và giá của vectơ vuông góc với nhau.
Vậy hai vectơ hai vectơ và không cùng phương.
b) Ta có: .
Xét điểm M(x; y) thuộc ∆. Vì nên
a(x – x0) + b(y – y0) = 0 ⇔ ax + by – ax0 – by0 = 0.
Xem thêm các bài giải bài tập Toán lớp 10 Cánh Diều hay, chi tiết khác:
Hoạt động 1 trang 73 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ...
Luyện tập 1 trang 75 Toán lớp 10 Tập 2: Cho đường thẳng Δ có phương trình tham số...
Hoạt động 3 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ...
Bài 3 trang 80 Toán lớp 10 Tập 2: Cho đường thẳng d có phương trình tham số là...
Bài 4 trang 80 Toán lớp 10 Tập 2: Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
