Với giải Câu hỏi trang 82 Toán 10 Tập 2 Cánh Diều trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 82 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
Luyện tập 1 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của hai đường thẳng
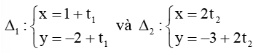
Lời giải:
Đường thẳng ∆1 có vectơ chỉ phương là .
Đường thẳng ∆2 có vectơ chỉ phương là .
Ta có: , do đó cùng phương.
Chọn t1 = 0, ta có điểm M(1; – 2) thuộc ∆1. Thay tọa độ điểm M vào phương trình ∆2, ta được:
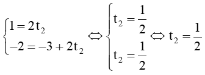
Vậy điểm M cũng thuộc ∆2.
Vậy hai đường thẳng ∆1 và ∆2 trùng nhau.
Δ1: 3x – 2y + 6 = 0;
Δ2: x + 2y + 2 = 0;
Δ3: 2x + 4y – 4 = 0.
Lời giải:
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆1 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ có nghiệm duy nhất là (x; y) = .
Do đó đường thẳng d cắt đường thẳng ∆1 tại điểm có tọa độ .
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆2 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ trên vô nghiệm.
Do đó đường thẳng d và đường thẳng ∆2 song song với nhau.
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆3 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ trên có vô số nghiệm.
Do đó, hai đường thẳng d và ∆3 có vô số điểm chung nên d trùng với ∆3.
Xem thêm các bài giải bài tập Toán lớp 10 Cánh Diều hay, chi tiết khác:
Hoạt động 1 trang 81 Toán lớp 10 Tập 2: Nêu vị trí tương đối của hai đường thẳng trong mặt phẳng...
Luyện tập 1 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của hai đường thẳng...
Luyện tập 4 trang 85 Toán lớp 10 Tập 2: a) Tính khoảng cách từ điểm O(0; 0) đến đường thẳng ∆: ...
Bài 1 trang 86 Toán lớp 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau...
Bài 5 trang 86 Toán lớp 10 Tập 2: Cho ba điểm A(2; – 1), B(1; 2) và C(4; – 2). Tính số đo góc BAC...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.