Với giải Câu hỏi trang 35 SBT Toán 10 Tập 1 Chân trời sáng tạo trong Bài tập cuối chương 2 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem: 

SBT Toán 10 Chân trời sáng tạo trang 35: Bài tập cuối chương 2

Bài 5 trang 35 SBT Toán 10 Tập 1: Biểu thức F = 2x – 8y đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?

A. – 48;

B. 0;

C. – 160;

D. – 40.

Lời giải:

Đáp án đúng là: A

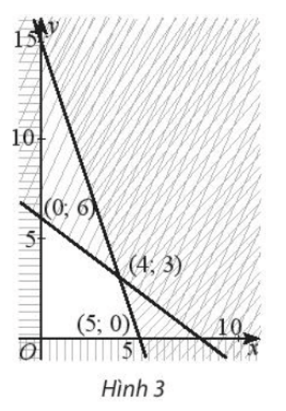
Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).

Người ta chứng minh được rằng biểu thức F = 2x – 8y đạt GTNN tại các đỉnh của đa giác.

Ta có: F(0; 0) = 2 . 0 – 8 . 0 = 0

F(0; 6) = 2 . 0 – 8 . 6 = – 48

F(4; 3) = 2 . 4 – 8 . 3 = – 16

F(5; 0) = 2 . 5 – 8 . 0 = 10

Vì – 48 < – 16 < 0 < 10.

Do đó, F đạt GTNN bằng – 48 tại đỉnh có tọa độ (0; 6).

Bài 6 trang 35 SBT Toán 10 Tập 1: Biểu thức F = 5x + 2y đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?

A. 30;

B. 12;

C. 25;

D. 26;

Lời giải:

Đáp án đúng là: D

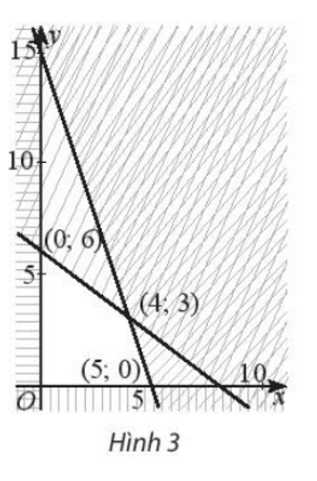
Miền đa giác không gạch chéo trong Hình 3 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3), (5; 0).

Người ta chứng minh được rằng biểu thức F = 5x + 2y đạt GTLN tại các đỉnh của đa giác.

Ta có: F(0; 0) = 5 . 0 + 2 . 0 = 0

F(0; 6) = 5. 0 + 2 . 6 = 12

F(4; 3) = 5 . 4 + 2 . 3 = 26

F(5; 0) = 5 . 5 + 2. 0 = 25

Vì 0 < 12 < 25 < 26.

Vậy F đạt GTLN bằng 26 tại đỉnh có tọa độ (4; 3).

II. TỰ LUẬN

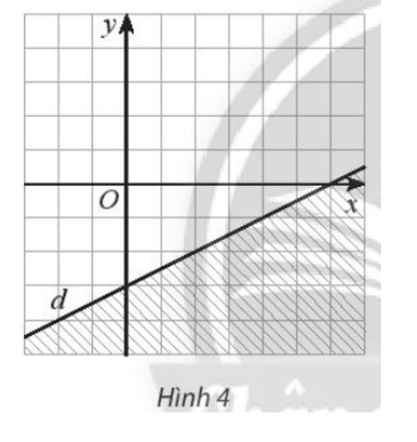
Bài 1 trang 35 SBT Toán 10 Tập 1: Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong Hình 4 (mỗi ô vuông có cạnh là 1 đơn vị).

Lời giải:

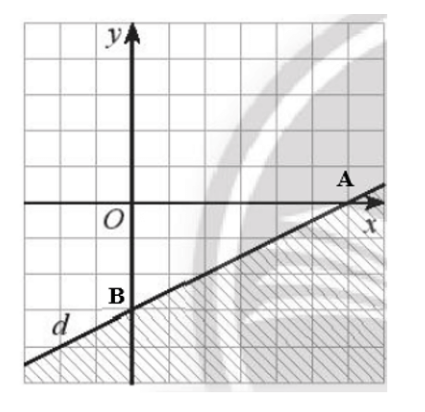
Gọi dạng đường thẳng d: y = ax + b.

Ta có đường thẳng d đi qua hai điểm A và B. Điểm A nằm trên tia Ox và cách O một khoảng bằng 6 cạnh ô vuông, do đó tọa độ A là A(6; 0). Điểm B nằm trên Oy và nằm phía dưới điểm O, cách O một khoảng 3 cạnh ô vuông nên B(0; – 3).

Khi đó ta có: $\left\{\begin{array}{l}0=6.a+b\\ -3=0.a+b\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{1}{2}\\ b=-3\end{array}\right.$.

Do đó d: y = $\frac{1}{2}$x – 3 hay d: x – 2y – 6 = 0.

Xét điểm O(0; 0) thuộc miền nghiệm của bất phương trình cần tìm.

Ta có: 0 – 2 . 0 – 6 = – 6 < 0.

Do đó, bất phương trình cần tìm có dạng x – 2y – 6 ≤ 0 (do miền nghiệm bao gồm cả bờ d).

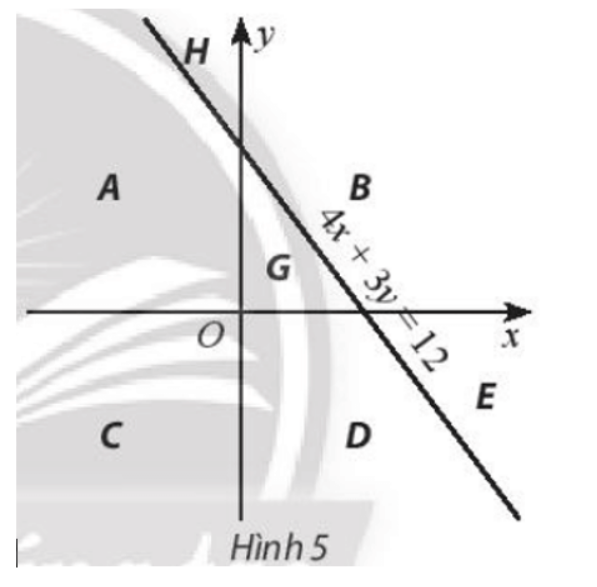
Bài 2 trang 35 SBT Toán 10 Tập 1: Đường thẳng 4x + 3y = 12 và hai trục tọa độ chia mặt phẳng Oxy thành các miền như Hình 5. Hãy tìm hệ bất phương trình có miền nghiệm là miền B (kể cả bờ).

Lời giải:

Quan sát Hình 5, ta thấy miền B (kể cả bờ) nằm bên trên trục Ox (là miền nghiệm của bất phương trình y ≥ 0), bên phải trục Oy (là miền nghiệm của bất phương trình x ≥ 0) và không chứa điểm O(0; 0), lại có 4 . 0 + 3 . 0 = 0 < 12, do đó miền B nằm trong miền nghiệm của bất phương trình 4x + 3y ≥ 12.

Do đó, hệ bất phương trình có miền nghiệm là miền B là $\left\{\begin{array}{l}4x+3y\ge 12\\ x\ge 0\\ y\ge 0\end{array}\right.$

Bài 3 trang 35 SBT Toán 10 Tập 1: Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây.

Trong các giá trị tìm được:

a) tìm GTLN của F.

b) tìm GTNN của G.

Lời giải:

+ Với x = 0, y = 2, ta có: F = 4 . 0 + 5 . 2 = 10, G = 5 . 0 – 3 . 2 = – 6.

+ Với x = 0, y = 4, ta có: F = 4 . 0 + 5 . 4 = 20, G = 5 . 0 – 3 . 4 = – 12.

+ Với x = 1, y = 0, ta có: F = 4 . 1 + 5 . 0 = 4, G = 5 . 1 – 3 . 0 = 5.

+ Với x = 1, y = 1, ta có: F = 4 . 1 + 5 . 1 = 9, G = 5 . 1 – 3 . 1 = 2.

+ Với x = 2, y = 0, ta có: F = 4 . 2 + 5 . 0 = 8, G = 5 . 2 – 3 . 0 = 10.

+ Với x = 2, y = 1, ta có: F = 4 . 2 + 5 . 1 = 13, G = 5 . 2 – 3 . 1 = 7.

+ Với x = 4, y = 0, ta có: F = 4 . 4 + 5 . 0 = 16, G = 5 . 4 – 3 . 0 = 20.

Vậy ta hoàn thành được bảng như sau:

Từ bảng trên ta có:

a) GTLN của F là 20.

b) GTNN của G là – 12.