Với giải Câu hỏi trang 74 SBT Toán 10 Tập 2 Cánh Diều trong Bài 3: Phương trình đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:
SBT Toán 10 Cánh Diều trang 74 Bài 3: Phương trình đường thẳng
Bài 31 trang 74 SBT Toán 10: Cho đường thẳng ∆: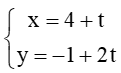 
và điểm A(2; 1). Hai điểm M, N nằm trên ∆.
a) Tìm tọa độ điểm M sao cho AM=
b) Tìm tọa độ điểm N sao cho đoạn thẳng AN ngắn nhất.
Lời giải:
a) Do M nằm trên ∆ nên M(4 + t; -1 + 2t).
Suy ra =(4+t-2;-1+2t-1) = (2+t;-2+2t)
Mà AM =
5t2-4t-9=0 
Vậy M hoặc M(3;-3).
b) Do N nằm trên ∆ nên N(4 + m; -1 + 2m).
Suy ra =(4+m-2;-1+2m-1) = (2+m;-2+2m)
AN ngắn nhất khi và chỉ khi N là hình chiếu của A lên ∆.
Khi đó vuông góc với vectơ chỉ phương của ∆: =(1;2)
Hay (2 + m). 1 + (-2 + 2m). 2 = 0
Suy ra .
Vậy .
a) Tìm tọa độ điểm M thuộc ∆ và cách đều hai điểm A và B.
b*) Tìm tọa độ điểm N thuộc ∆ sao cho || có giá trị nhỏ nhất.
Lời giải:
a) Do M thuộc đường thẳng ∆ nên M(t; 4 – 2t).
Suy ra =(t+2;2-2t) và =(t-7;-1-2t).
Do M cách đều 2 điểm A, B nên MA = MB.
Hay ||= ||
⇔ 5t2 – 4t + 8 = 5t2 – 10t + 50
⇔ 6t = 42
⇔ t = 7
Vậy M(7; -10).
b) Do N thuộc đường thẳng ∆ nên N(m; 4 – 2m).
Suy ra =(-2-2;2m-2), =(7-m;2m+1) và =(4-1;2m-9)
= (9-3m;6m-10)
Gọi A= (9-3m)2+(6m-10)2
A=45m2 - 174m+181=45
Suy ra GTNN của || là đạt được khi m=
Hay .
Xem thêm các bài giải sách bài tập Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 26 trang 73 SBT Toán 10: Cho đường thẳng ∆: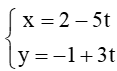 
. Trong các điểm có tọa độ dưới đây...,
Bài 29 trang 73 SBT Toán 10: Cho tam giác ABC, biết tọa độ trung điểm các cạnh BC, CA, AB.
Bài 31 trang 74 SBT Toán 10: Cho đường thẳng ∆: 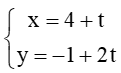và điểm A(2; 1). Hai điểm M, N nằm trên ∆....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
. Vectơ nào dưới đây là một vectơ chỉ phương của ∆?..
. Phương trình nào dưới đây là phương trình tổng quát của ∆
