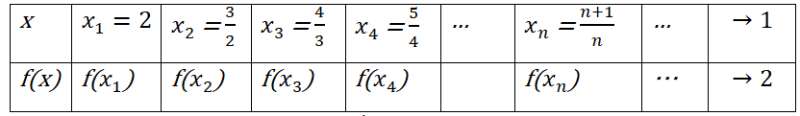Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 2: Giới hạn của hàm số chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về giới hạn của hàm số lớp 11.
Giải bài tập Toán 11 Bài 2: Giới hạn của hàm số
Trả lời câu hỏi giữa bài:
Câu hỏi 1 trang 123 SGK Đại số và Giải tích 11: Xét hàm số: . Cho biến những giá trị khác 1 lập thành dãy số như trong bảng sau:
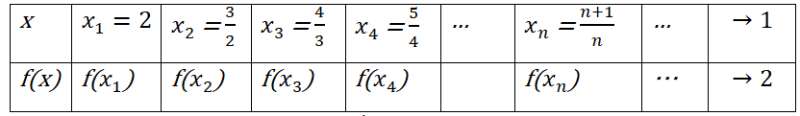
Khi đó, các giá trị tương ứng của hàm số
cũng lập thành một dãy số mà ta kí hiệu là
a) Chứng minh rằng
b) Tìm giới hạn của dãy số
c) Chứng minh rằng với dãy số bất kì và , ta luôn có
(Với tính chất thể hiện trong câu 2, ta nói hàm số có giới hạn là 2 khi dần tới 1).
Phương pháp giải:
a) Tính và rút gọn suy ra đáp số, chú ý .
b) Xét giới hạn và suy ra đáp số.
c) Tính dựa vào công thức có được ở phần 1a.
Lời giải:
a)
b)
Ta có:
c) .
Câu hỏi 2 trang 127 SGK Đại số và Giải tích 11: Trong biểu thức (1) xác định hàm số ở Ví dụ 4, cần thay 2 bằng số nào để hàm số có giới hạn là -2 khi
Phương pháp giải:
Để hàm số có giới hạn bằng -2 tại x = 1 thì .
Lời giải:
Để hàm số có giới hạn bằng tại thì hay .
Vậy cần thay bằng để hàm số có giới hạn bằng tại .
Câu hỏi 3 trang 127 SGK Đại số và Giải tích 11: Cho hàm số có đồ thị như ở Hình 52

Quan sát đồ thị và cho biết:
- Khi biến dần tới dương vô cực, thì dần tới giá trị nào.
- Khi biến dần tới âm vô cực, thì dần tới giá trị nào.
Lời giải:
- Khi biến dần tới dương vô cực, thì dần tới giá trị dương vô cực.
- Khi biến dần tới âm vô cực, thì dần tới giá trị âm vô cực.
Bài tập trang 132, 133 SGK Toán 11
Bài 1 trang 132 SGK Đại số và Giải tích 11: Dùng định nghĩa tìm các giới hạn sau:
a) ;
b).
Phương pháp giải:
a)
xác định trên
+) Lấy dãy bất kì, :
+) Tính .
b)
.
+) Lấy dãy bất kì:
+) Tính .
Lời giải:
a)
Hàm số xác định trên và ta có
Giả sử là dãy số bất kì và ; và khi hay
Ta có
Vậy = .
b)
Hàm số = xác định trên .
Giả sử là dãy số bất kì và khi hay
Ta có
Vậy .
Bài 2 trang 132 SGK Đại số và Giải tích 11: Cho hàm số . Và các dãy số với , với . Tính , , và . Từ đó có kết luận gì về giới hạn của hàm số đã cho khi ?
Phương pháp giải:
- Sử dụng giới hạn cơ bản với
- Thay vào và tính giới hạn.
Lời giải:
Do nên .
nên .
Do đó nên không tồn tại giới hạn của hàm số tại .
Vậy hàm số đã cho không có giới hạn khi .
Bài 3 trang 132 SGK Đại số và Giải tích 11: Tính các giới hạn sau:
a) ;
b) ;
c) ;
d) ;
e) ;
f) .
Phương pháp giải:
Nếu hàm số xác định tại thì .
Nếu giới hạn hàm số có dạng vô định, tìm cách khử dạng vô định.
Lời giải:
a)
= .
b)
= = .
c)
=
= = .
d)
.
e)
vì:
Cách khác:
f)
Vì ; khi
và
Vậy
Cách khác:
Mà
và
Nên .
Bài 4 trang 132 SGK Đại số và Giải tích 11: Tính các giới hạn sau:
a) ;
b) ;
c) .
Phương pháp giải:
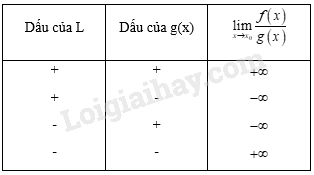
a) Sử dụng quy tắc tìm giới hạn của thương
|
|
|
Dấu của
|
|
|
|
|
Tùy ý
|
0
|
|
|
0
|
+
|
|
|
-
|
|
|
|
+
|
|
|
-
|
|
b)
Sử dụng quy tắc tìm giới hạn của thương
|
|
|
Dấu của
|
|
|
|
|
Tùy ý
|
0
|
|
|
0
|
+
|
|
|
-
|
|
|
|
+
|
|
|
-
|
|
c)
Sử dụng quy tắc tìm giới hạn của thương
|
|
|
Dấu của
|
|
|
|
|
Tùy ý
|
0
|
|
|
0
|
+
|
|
|
-
|
|
|
|
+
|
|
|
-
|
|
Lời giải:
a)
Ta có và với và .
Do đó .
b)
Ta có và với và .
Do đó .
c)
Ta có và với và .
Do đó .
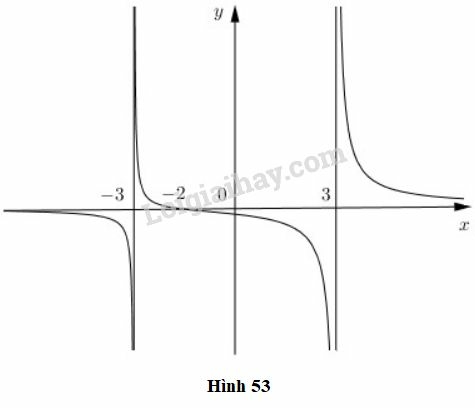
Bài 5 trang 133 SGK Đại số và Giải tích 11: Cho hàm số có đồ thị như trên hình 53.
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi , và .
b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
với được xét trên khoảng ,
với được xét trên khoảng ,
với được xét trên khoảng .
Phương pháp giải:
a) Quan sát đồ thị hàm số.
b) Tính các giới hạn, sử dụng quy tắc tính giới hạn được học và kết luận.
Lời giải:
a)
Quan sát đồ thị ta thấy thì ; khi thì ;
khi thì .
b)
+)
Mà
và
nên
+)
Vì và ; khi
nên .
+)
Vì và ; khi
nên .
Cách khác:
= .
=
vì = và .
= .
vì = = và .
Bài 6 trang 133 SGK Đại số và Giải tích 11: Tính:
a);
b);
c);
d) .
Phương pháp giải:
Sử dụng quy tắc tìm giới hạn của tích .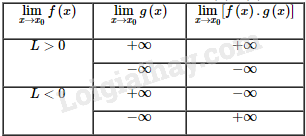
Lời giải:
a)
b)
c)
d)
Bài 7 trang 133 SGK Đại số và Giải tích 11: Một thấu kính hội tụ có tiêu cự là . Gọi và lần lượt là khoảng cách từ một vật thật và từ ảnh của nó tới quang tâm của thấu kính (h.54). Công thức thấu kính là
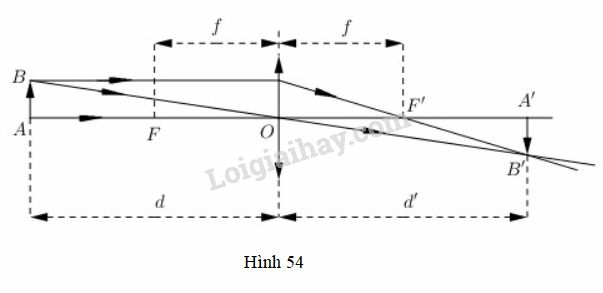
a) Tìm biểu thức xác định hàm số .
b) Tìm , và . Giải thích ý nghĩa của các kết quả tìm được.
Phương pháp giải:
a) Sử dụng công thức .
b) Sử dụng quy tắc tìm giới hạn của thương.
Lời giải:
a)
Vậy .
b)
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+)
= .
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).
Lý thuyết Bài 2: Giới hạn của hàm số
I. Các dạng vô định
1. Dạng vô định
Bài toán:
Tính khi , trong đó là các đa thức hoặc căn thức.
Phương pháp:
- Bước 1: Phân tích tử và mẫu thành tích các nhân tử.
- Bước 2: Chia cả tử và mẫu cho nhân tử chung của tử và mẫu.
- Bước 3: Tính giới hạn theo cách thông thường.
Nếu và có chứa căn thức thì có thể nhân cả tử và mẫu với biểu thức liên hợp trước khi phân tích chúng thành tích và giản ước.
Đặc biệt:
Ví dụ:
2. Dạng vô định
Bài toán: Tính khi , trong đó là các đa thức.
Phương pháp:
- Bước 1: Đặt lũy thừa bậc cao nhất của tử và mẫu ra làm nhân tử chung.
- Bước 2: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của .
- Bước 3: Tính các giới hạn thông thường và suy ra kết quả.
Ví dụ:
Cần xét xem khi khai căn biểu thức có chứa căn bậc hai.
3. Dạng vô định
Bài toán: Tính giới hạn khi và .
Phương pháp:
- Bước 1: Biến đổi để đưa về dạng hoặc để đưa về dạng .
- Bước 2: Sử dụng các phương pháp của dạng 1 và 2 để tính tiếp giới hạn.
4. Dạng vô định
Bài toán: Tính khi hoặc tính khi .
Phương pháp:
- Bước 1: Nhận hoặc chia với biểu thức liên hợp (nếu có căn thức) hoặc quy đồng để đưa về cùng một phân thức.
- Bước 2: Thực hiện tính giới hạn dựa theo các dạng đã biết.
II. Giới hạn của hàm số
1. Giới hạn hữu hạn
+) Cho khoảng chứa điểm và hàm số xác định trên hoặc trên
khi và chỉ khi với dãy số bất kì, và , ta có
.
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi dãy số \((xn) bất kì, và ,ta có .
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi với dãy số bất kì, và , ta có
.
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi với dãy số bất kì, , thì .
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi với dãy số bất kì, , thì .
2. Giới hạn vô cực
Sau đây là hai trong số nhiều loại giới hạn vô cực khác nhau:
+) Cho hàm số xác định trên khoảng , khi và chỉ khi với dãy số bất kì, , thì ta có
+) Cho khoảng chứa điểm và hàm số xác định trên hoặc trên
và chỉ khi với dãy số bất kì, và thì ta có: .
Nhận xét: có giới hạn khi và chỉ khi có giới hạn .
3. Các giới hạn đặc biệt
a) ;
b) ;
c) ;
d) ( là hằng số);
e) , với nguyên dương;
f) , nếu là số lẻ;
g) , nếu là số chẵn.
4. Định lí về giới hạn hữu hạn
Định lí 1.
a) Nếu và thì:
;
;
;
= (nếu ).
b) Nếu và , thì và
Chú ý: Định lí 1 vẫn đúng khi hoặc .
Định lí 2.
khi và chỉ khi f(x) = .
5. Quy tắc về giới hạn vô cực
a) Quy tắc giới hạn của tích
+ Nếu và thì được cho trong bảng sau:
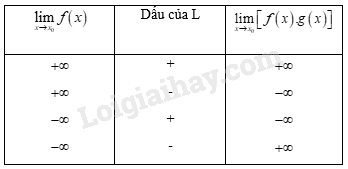
b) Quy tắc tìm giới hạn của thương
+ Nếu và và hoặc với mọi , trong đó là một khoảng nào đó chứa thì được cho trong bảng sau: