Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 3: Hàm số liên tục chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về hàm số liên tục lớp 11.

Giải bài tập Toán 11 Bài 3: Hàm số liên tục

Trả lời câu hỏi giữa bài:

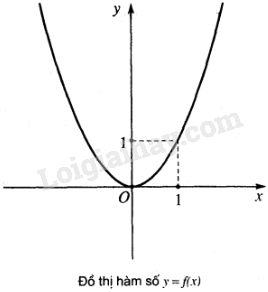
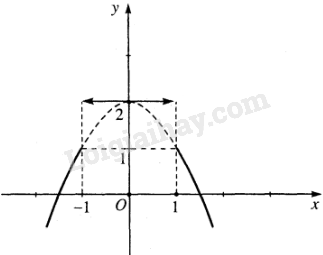
a) Tính giá trị của mỗi hàm số tại $x=1$ và so sánh với giới hạn (nếu có) của hàm số đó khi $x\to 1$;

b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ $x=1$.

Phương pháp giải:

a) Thay $x=1$ vào lần lượt hai hàm số và tính giá trị.

b) Quan sát đồ thị và nhận xét.

Lời giải:

a)

$f(1)=1^2=1=\underset{x\to 1}{lim}f(x)$

Vì $x=1$ nên $g(1)=-1^2+1=-1+1=0$

Lại có: $\underset{x\to 1^{+}}{lim}g\left(x\right)=\underset{x\to 1^{+}}{lim}\left(-x^2+2\right)=1$ và $\underset{x\to 1^{-}}{lim}g\left(x\right)=\underset{x\to 1^{-}}{lim}\left(2\right)=2$ nên $\underset{x\to 1^{-}}{lim}g\left(x\right)\ne \underset{x\to 1^{+}}{lim}g\left(x\right)$ và không tồn tại giới hạn $\underset{x\to 1}{lim}g\left(x\right)$.

b)

Đồ thị hàm số $f(x)$ liên tục tại $x=1$.

Đồ thị hàm số $g(x)$ gián đoạn tại $x=1$.

Lời giải:

Để hàm số liên tục trên $\mathbb{R}$ thì nó phải liên tục tại $x=1$ hay $\underset{x\to 1}{lim}h\left(x\right)=h\left(1\right)$ $\iff h\left(1\right)=2$.

Vậy cần thay số $5$ bằng số $2$ để hàm số liên tục trên $\mathbb{R}$.

Hỏi đồ thị của hàm số có cắt trục hoành tại điểm thuộc khoảng $(a;b)$ không?

⦁ Bạn Hưng trả lời rằng: “Đồ thị của hàm số $y=f(x)$ phải cắt trục hoành $Ox$ tại một điểm duy nhất nằm trong khoảng $(a;b)$”.

⦁ Bạn Lan khẳng định: “Đồ thị của hàm số $y=f(x)$ phải cắt trục hoành $Ox$ ít nhất tại một điểm nằm khoảng $(a;b)$”.

⦁ Bạn Tuấn thì cho rằng: “Đồ thị của hàm số $y=f(x)$ có thể không cắt trục hoành trong khoảng $(a;b)$, chẳng hạn như đường parabol ở hình (h.58).

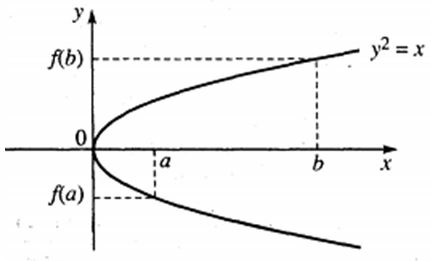
Câu trả lời của bạn nào đúng, vì sao?

Lời giải:

- Bạn Lan nói đúng vì $f(a)$ và $f(b)$ trái dấu nên tồn tại ít nhất 1 giá trị $x$ sao cho $f(x)=0$, do đó đồ thị hàm số $y=f(x)$ cắt trục hoành tại ít nhất 1 điểm.

- Bạn Hưng sai vì có thể có 2 giá trị x sao cho $f(x)=0$

- Đường parabol trên hình 58 là đồ thị hàm số $y^2=x$ ⇒ đồ thị hàm số $y=f(x)$ sẽ là 1 nửa nằm trên hoặc 1 nửa nằm dưới trục hoành

Khi đó $f(a)$ và $f(b)$ cùng dấu, mâu thuẫn với điều kiện $f(a)$ và $f(b)$ trái dấu

Ví dụ của Tuấn sai.

Lời giải:

Ta có: $f\left(x\right)=x^3+2x-5$.

Chọn $a={\displaystyle \frac{5}{4}},b={\displaystyle \frac{7}{4}}$ thỏa mãn $1<a<b<2$.

Ta thấy: $f\left({\displaystyle \frac{5}{4}}\right)=-{\displaystyle \frac{35}{64}}<0,$ $f\left({\displaystyle \frac{7}{4}}\right)={\displaystyle \frac{247}{64}}>0$ nên $f\left({\displaystyle \frac{5}{4}}\right).f\left({\displaystyle \frac{7}{4}}\right)<0$.

Vậy trong khoảng $\left({\displaystyle \frac{5}{4}};{\displaystyle \frac{7}{4}}\right)$ thì phương trình $f\left(x\right)=0$ có ít nhất một nghiệm.

Bài tập trang 140, 141 SGK Toán 11

Bài 1 trang 140 SGK Đại số và Giải tích 11:Dùng định nghĩa xét tính liên tục của hàm số $f(x)=x^3+2x-1$ tại $x_0=3$.

Phương pháp giải:

Hàm số $y=f(x)$ có tập xác định $D$ liên tục tại $x_0\in D$

$\iff \underset{x\to x_0}{lim}f\left(x\right)=f\left(x_0\right)$.

Lời giải:

Hàm số $f(x)=x^3+2x-1$ xác định trên $\mathbb{R}$ và $x_0=3\in \mathbb{R}$.

Ta có: $\{\begin{array}{l}\underset{x\to 3}{lim}f\left(x\right)=3^3+2.3-1=32\\ f\left(3\right)=3^3+2.3-1=32\end{array}$ $\Rightarrow \underset{x\to 3}{lim}f\left(x\right)=f\left(3\right)$.

Vậy hàm số đã cho liên tục tại điểm $x_0=3$.

$$g(x)=\{\begin{array}{cc}{\displaystyle \frac{x^3-8}{x-2}};& x\ne 2\\ 5;& x=2\end{array}$$

b) Trong biểu thức xác định $g(x)$ ở trên, cần thay số $5$ bởi số nào để hàm số liên tục tại $x_0=2$.

Phương pháp giải:

Hàm số $y=f(x)$ có tập xác định $D$ liên tục tại $x_0\in D$

$\iff \underset{x\to x_0}{lim}f\left(x\right)=f\left(x_0\right)$.

Lời giải:

a) Ta có:

$\begin{array}{l}\underset{x\to 2}{lim}g\left(x\right)=\underset{x\to 2}{lim}{\displaystyle \frac{x^3-8}{x-2}}\\ =\underset{x\to 2}{lim}{\displaystyle \frac{(x-2)(x^2+2x+4)}{x-2}}\\ =\underset{x\to 2}{lim}\left(x^2+2x+4\right)\\ =2^2+\mathrm{2.2.}+4=12\\ g\left(2\right)=5\\ \Rightarrow \underset{x\to 2}{lim}g\left(x\right)\ne g\left(2\right)\end{array}$

Vì $\underset{x\to 2}{lim}g(x)\ne g(2)$ nên hàm số $y=g(x)$ gián đoạn tại $x_0=2$.

b)

Để hàm số $y=g(x)$ liên tục tại $x_0=2$ $\Rightarrow \underset{x\to 2}{lim}g\left(x\right)=g\left(2\right)=12\Rightarrow$ ta cần thay số $5$ bởi số $12$.

a) Vẽ đồ thị của hàm số $y=f(x)$. Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

b) Khẳng định nhận xét trên bằng một chứng minh.

Phương pháp giải:

a) Khi $x<-1$, vẽ đường thẳng $y=3x+2$.

    Khi $x\ge -1$, vẽ parabol $y=x^2-1$.

Lưu ý: Vẽ trên cùng một hệ trục tọa độ.

Nhận xét về tính liên tục của hàm số (Đồ thị hàm số có bị gãy khúc tại điểm nào không?)

b) Hàm số $y=f(x)$ liên tục tại điểm $x_0$ $\iff \underset{x\to x_0}{lim}f\left(x\right)=f\left(x_0\right)$.

Lời giải:

a)

Khi $x<-1$, đồ thị hàm số là đường thẳng $y=3x+2$, khi $x\ge -1$ đồ thị hàm số là parabol $y=x^2-1$.

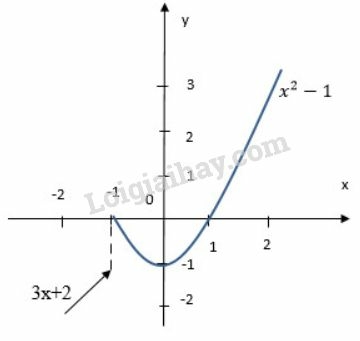
Đồ thị hàm số $y=f(x)$ là một đường không liền nét mà bị đứt quãng tại $x_0=-1$. Vậy hàm số đã cho liên tục trên khoảng $(-\infty ;-1)$ và $(-1;+\infty )$.

b)

+) Nếu $x<-1$: $f(x)=3x+2$ liên tục trên $(-\infty ;-1)$ (vì đây là hàm đa thức nên liên tục trên tập xác định của nó).

+) Nếu $x>-1$: $f(x)=x^2-1$ liên tục trên $(-1;+\infty )$ (vì đây là hàm đa thức nên liên tục trên tập xác định của nó).

+) Xét tính liên tục của hàm số tại $x=-1$;

Ta có 

$\underset{x\to -1^{-}}{lim}f(x)=$$\underset{x\to -1^{-}}{lim}(3x+2)=3(-1)+2=-1$.

$\underset{x\to -1^{+}}{lim}f(x)=\underset{x\to -1^{+}}{lim}(x^2-1)$$=(-1{)}^2-1=0$.

Vì $\underset{x\to -1^{-}}{lim}f(x)\ne \underset{x\to -1^{+}}{lim}f(x)$ nên không tồn tại $\underset{x\to -1}{lim}f(x)$.

Vậy hàm số gián đoạn tại $x_0=-1$.

Phương pháp giải:

Hàm phân thức, hàm lượng giác liên tục trên các khoảng xác định của chúng.

Lời giải:

+) Hàm số $f(x)={\displaystyle \frac{x+1}{x^2+x-6}}$ xác định khi và chỉ khi:

$x^2+x-6\ne 0\iff \{\begin{array}{l}x\ne -3\\ x\ne 2\end{array}$ $\Rightarrow D=R\mathrm{\setminus }\left\{-3;2\right\}$

Hàm số $f(x)$ là hàm phân thức nên liên tục trên các khoảng xác định.

Vậy f(x) liên tục trên các khoảng $(-\infty ;-3),(-3;2)$ và $(2;+\infty )$

+) Hàm số $g\left(x\right)=\tan x+\sin x$ xác định khi và chỉ khi 

$\cos x\ne 0\iff x\ne {\displaystyle \frac{\pi }{2}}+k\pi \left(k\in Z\right)$

Hàm số $g(x)$ là hàm lượng giác nên liên tục trên các khoảng xác định.

Vậy g(x) liên tục trên các khoảng $(-{\displaystyle \frac{\pi }{2}}+k\pi ;{\displaystyle \frac{\pi }{2}}+k\pi )$ với $k\in \mathbb{Z}$.

"Nếu hàm số $y=f(x)$ liên tục tại điểm $x_0$ còn hàm số $y=g(x)$ không liên tục tại $x_0$ thì $y=f(x)+g(x)$ là một hàm số không liên tục tại $x_0$" .

Phương pháp giải:

Chứng minh phản chứng: giả sử ngược lại hàm số $y=f\left(x\right)+g\left(x\right)$ là hàm số liên tục tại x0, chứng minh điều này là vô lý.

Lời giải:

Đúng, vì:

Giả sử ngược lại: hàm số $y=f(x)+g(x)$ liên tục tại $x_0$.

Đặt $h(x)=f(x)+g(x)$ liên tục tại $x=x_0$.

$\Rightarrow g(x)=h(x)-f(x)$.

Vì $y=h(x)$ và $y=f(x)$ liên tục tại $x_0$ $\Rightarrow h\left(x\right);-f\left(x\right)$ liên tục tại $x_0$.

Theo giả sử ta có hàm số $h\left(x\right)+\left(-f\left(x\right)\right)=h\left(x\right)-f\left(x\right)=g\left(x\right)$ phải liên tục tại $x_0$. Điều này trái với giả thiết.

Vậy giả sử ban đầu sai, tức là $y=f(x)+g(x)$ không liên tục tại $x_0$.

a) $2x^3-6x+1=0$ có ít nhất hai nghiệm;

b) $\cos x=x$ có nghiệm.

Phương pháp giải:

- Xét các hàm số vế trái của phương trình.

- Tìm hai điểm bất kì và tính tích các giá trị của hàm số tại hai điểm đó.

+ Nếu tích nhỏ hơn $0$ thì ta kết luận phương trình có ít nhất một nghiệm trong khoảng hai giá trị ấy.

+ Nếu tích lớn hơn $0$ thì ta không kết luận gì và tìm giá trị khác để tính.

Lời giải:

a) Xét hàm số $f(x)=2x^3-6x+1$ là hàm đa thức nên liên tục trên $\mathbb{R}$.

Ta có:

$f\left(0\right)={2.0}^3-6.0+1=1;$

$f\left(1\right)={2.1}^3-6.1+1=-3;$

$f\left(-2\right)=2.{\left(-2\right)}^3-6.\left(-2\right)+1=-3$

+) $f\left(0\right).f\left(1\right)=1.\left(-3\right)<0$ nên phương trình có ít nhất 1 nghiệm $x_0\in (0;1)$.

+) $f\left(0\right).f\left(-2\right)=1.\left(-3\right)<0$ nên phương trình có ít nhất 1 nghiệm $x_1\in (-2;0)$.

Mà $\left(0;1\right)\cup \left(-2;0\right)=\mathrm{\varnothing }\Rightarrow x_0\ne x_1\Rightarrow$ phương trình $f(x)=0$ có ít nhất hai nghiệm.

b) $\cos x=x\iff \cos x-x=0$

Xét hàm số $g\left(x\right)=\cos x-x$ xác định trên $\mathbb{R}$ nên liên tục trên $\mathbb{R}$.

Ta có:

$g\left(0\right)=\cos 0-0=1-0=1;$

$g\left({\displaystyle \frac{\pi }{2}}\right)=\cos {\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{\pi }{2}}=-{\displaystyle \frac{\pi }{2}}$

$g\left(0\right).g\left({\displaystyle \frac{\pi }{2}}\right)=1.\left(-{\displaystyle \frac{\pi }{2}}\right)=-{\displaystyle \frac{\pi }{2}}<0$ nên phương trình đã cho có ít nhất 1 nghiệm thuộc khoảng $(0;{\displaystyle \frac{\pi }{2}})$.

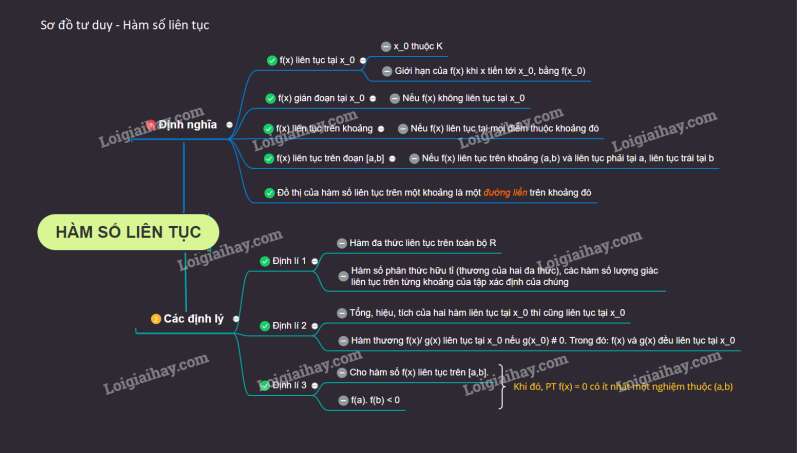
Lý thuyết Bài 3: Hàm số liên tục