Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Giới hạn của dãy số (Lý thuyết + 35 bài tập có lời giải) Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.
Nội dung bài viết
Mời các bạn đón xem:
Giới hạn của dãy số (Lý thuyết + 35 bài tập có lời giải)
I. Lý thuyết Giới hạn của dãy số
Ta nói dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực, nếu |un| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: ![]() hay un → 0 khi n → +∞.
hay un → 0 khi n → +∞.
Định nghĩa 2
Ta nói dãy số (vn) có giới hạn là a (hay vn dần tới a) khi n → +∞ nếu ![]()
Kí hiệu: ![]() hay vn → a khi n → +∞.
hay vn → a khi n → +∞.
a) ![]() với k nguyên dương;
với k nguyên dương;
b) ![]() nếu |q| < 1;
nếu |q| < 1;
Chú ý: Từ nay về sau thay cho ![]() ta viết tắt là lim un = a.
ta viết tắt là lim un = a.
Định lí 1
a) Nếu lim un = a và lim vn = b thì
lim (un + vn) = a + b
lim (un – vn) = a – b
lim (un.vn) = a.b
![]()
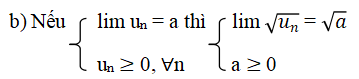
Cấp số nhân vô hạn (un) có công bội q, với |q| < 1 được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn:
1. Định nghĩa
c) Nếu un = c (c là hằng số) thì ![]()
- Ta nói dãy số (un) có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim un = +∞ hay un → +∞ khi n → +∞.
- Dãy số (un) có giới hạn là –∞ khi n → +∞, nếu lim (–un) = +∞.
Kí hiệu: lim un = –∞ hay un → –∞ khi n → +∞.
Nhận xét: un = +∞ ⇔ lim(–un) = –∞
2. Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau
a) lim nk = +∞ với k nguyên dương;
b) lim qn = +∞ nếu q > 1.
3. Định lí 2
a) Nếu lim un = a và lim vn = ±∞ thì ![]()
b) Nếu lim un = a > 0, lim vn = 0 và vn > 0, ∀ n > 0 thì
c) Nếu lim un = +∞ và lim vn = a > 0 thì
II. Bài tập Giới hạn của dãy số
Câu 1: Cho cấp số nhân un=12n∀n≥1 .Khi đó:
A. S=1
B. S=12n
C. S=0
D. S=2
Đáp án: A
Câu 2: Dãy số nào sau đây có giới hạn 0 ?
A. un=n2
B. un=2n
C. un=n
D. un=√n
Đáp án: B
Câu 3: Cho (un) là một cấp số nhân công bội q=13 và số hạng đầu u1=2,
Đặt S=u1+u2+...+un . Giá limSn là:
A. 1
B. 23
C. 43
D. 3
Đáp án: D
Câu 4: Cấp số nhân (un) có u1=2,u2=1. Đặt Sn=u1+u2+...+un ), khi đó:
A. Sn=4(1−12n)
B. Sn=4
C. Sn=2
D. Sn=(1−12n)
Đáp án: A
Câu 5: Giá trị của C=lim√3.3n+4n3n+1+4n+1 bằng:
A. +∞
B. 12
C. 0
D. 1
Đáp án: B
Câu 6: Biết limun=3. Chọn mệnh đề đúng trong các mệnh đề sau.
A. lim3un−1un+1=3
B. lim3un−1un+1=−1
C. lim3un−1un+1=2
D. lim3un−1un+1=1
Đáp án: C
Câu 7: Biết limun=+∞. Chọn mệnh đề đúng trong các mệnh đề sau.
A. limun+13u2n+5=1
B. limun+13u2n+5=0
C. limun+13u2n+5=13
D. limun+13u2n+5=+∞
Đáp án: B
Câu 8: Cho hai dãy số (un) , (vn) với un=1n,vn=(−1)nn.
Biết |(−1)nn|≤1n. Chọn kết luận không đúng:
A. limun=0
B. limvn=0
C. limun−limvn=0
D. Không tồn tại
Đáp án: D
Câu 9: Giới hạn lim(3.2n+1−5.3n+7n) bằng :
A. −∞.
B. +∞.
C. 3.
D. −5.
Đáp án: A
Câu 10: Giới hạn lim(2−5n)3(n+1)22−25n5 bằng?
A. −4.
B. −1.
C. 5.
D. −32.
Đáp án: C
Câu 11: Giá trị của lim(2n2+1)4(n+2)9n17+1 bằng:
A. +∞
B. −∞
C. 16
D. 1
Đáp án: C
Câu 12: Chọn kết luận không đúng:
A. lim12n=0
B. lim13n=0
C. lim10,5n=0
D. lim1(√2)n=0
Đáp án: C
Câu 13: Cho dãy số (un) có giới hạn L=−12. Chọn kết luận đúng:
A. lim(un+12)=12
B. lim(un+12)=0
C. lim(un−12)=0
D. lim(un−12)=12
Đáp án: B
Câu 14: Cho dãy số (un) với un=(1−122).(1−132)...(1−1n2). Khi đó lim(un) bằng?
A. 43
B. 12
C. 1.
D. 2
Đáp án: B
Câu 15: Giá trị của D=lim(√n2+2n−3√n3+2n2) bằng:
A. +∞
B. −∞
C. 13
D. 1
Đáp án: C
Câu 16: Cho các dãy số (un), (vn)có limun=53, limvn=−23. Chọn đáp án đúng:
A. lim(un−2vn)=13
B. lim(2un−vn)=4
C. lim(un−vn)=1
D. lim(un+vn)=13
Đáp án: B
Câu 17: Cho un=1−4n5n. Khi đó lim un bằng?
A. 15
B. −45
C. 45
D. −15
Đáp án: B
Câu 18: Cho un=n2−3n1−4n3. Khi đó limun bằng?
A. 0
B. −14
C. 34
D. −34
Đáp án: A
Câu 19: Cho un=3n+5n5n. Khi đó limun bằng?
A. 0.
B. 1.
C. 35.
D. +∞.
Đáp án: B
Câu 20: Giá trị lim(n3−2n+1) bằng
A. 0
B. 1
C. −∞
D. +∞
Đáp án: D
Câu 21: Giá trị lim(5n−n2+1) bằng
A. +∞
B. −∞
C. 5
D. −1
Đáp án: B
Câu 22. Giới hạn lim(√n2−n−n) bằng?
A. −∞.
B. −12.
C. 0.
D. +∞.
Đáp án: B
Câu 23: Giá trị của B=lim(3√n3+9n2−n) bằng:
A. +∞
B. −∞
C. 0
D. 3
Đáp án: D
Câu 24: Cho dãy số (un) với
un=11.3+13.5+...+1(2n−1)(2n+1)+ 1. Khi đó lim(un)bằng?
A. 12
B. 14
C. 1
D. 2
Đáp án: A
Câu 25: Giá trị lim(−1)nn(n+1) bằng
A. −1.
B. 1.
C. +∞.
D. 0.
Đáp án: D
Câu 26. Giới hạn lim(√n2−n+1−√n2+1) bằng?
A. 0.
B. −12
C. −1√2
D. 1√2
Đáp án: B
Câu 27: Giới hạn lim2n2−n+4√2n4−n2+1 bằng?
A. 1
B. √2
C. 2
D. 1√2
Đáp án: B
Câu 28: Cho các số thực a, b thỏa |a|<1;|b|<1.
Tìm giới hạn I=lim1+a+a2+...+an1+b+b2+...+bn
A. +∞
B. 1−a1−b
C. 1−b1−a
D. 1
Đáp án: C
Câu 29: Cho dãy số (un) xác định bởi {u1=2un+1=un+12,(n≥1). Khi đó mệnh đề nào sau đây là đúng?
A. Dãy (un) là dãy giảm tới 1 khi n→+∞.
B. Dãy (un) là dãy tăng tới 1 khi n→+∞.
C. Không tồn tại giới hạn của dãy (un).
D. Cả 3 đáp án trên đều sai.
Đáp án: C
Câu 30: Tính giới hạn của dãy số un=q+2q2+...+nqn với |q|<1
A. +∞
B. −∞
C. q(1−q)2
D. q(1+q)2
Đáp án: C
Câu 31: Tính lim(5n - n2 + 1)
A. +∞
B. -∞
C. 5.
D. -1
Đáp án: B
Câu 32: Tính lim un, với
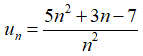
B. 0
C. 3
D. - 7
Đáp án: A
Câu 33: Tính lim un với 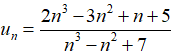 ?
?
A. – 3
B. 1
C. 2
D. 0
Đáp án: C
Câu 34: Giới hạn của dãy số (un) với 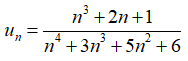 bằng
bằng
A. 1
B. 0
C. +∞
D. -∞
Đáp án: B
Câu 35: Giới hạn của dãy số (un) với 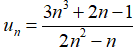 , bằng
, bằng
A. 3/2
B. 0
C. +∞.
D. 1
Đáp án: C
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.