Toptailieu biên soạn và giới thiệu lời Giải Toán 11 Bài 4: Phương trình lượng giác cơ bản hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 11 Bài 4 từ đó học tốt môn Toán 11.
Giải Toán 11 Bài 4: Phương trình lượng giác cơ bản
Lời giải:
Sau bài học này ta sẽ giải quyết được bài toán trên như sau:
Chọn hệ trục tọa độ có gốc tọa độ đặt tại vị trí khẩu pháo, trục Ox theo hướng khẩu pháo như hình dưới đây.
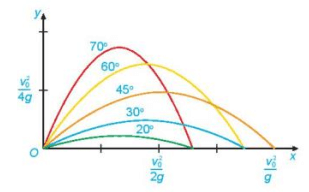
Khi đó theo Vật lí, ta biết rằng quỹ đạo của quả đạn pháo có dạng đường parabol có phương trình (với g là gia tốc trọng trường).
Cho y = 0 ta được , suy ra x = 0 hoặc .
Quả đạn tiếp đất khi .
Ta có , dấu bằng xảy ra khi sin 2α = 1.
Giải phương trình sin 2α = 1, ta được α = .
Do nên hay α = 45°.
Vậy quả đạn pháo sẽ bay xa nhất khi góc bắn bằng 45°.
HĐ1 trang 31 Toán 11 Tập 1: Nhận biết khái niệm hai phương trình tương đương
Cho hai phương trình 2x – 4 = 0 và (x – 2)(x2 + 1) = 0.
Tìm và so sánh tập nghiệm của hai phương trình trên.
Lời giải:
+) Ta có: 2x – 4 = 0, suy ra x = 2.
Vậy tập nghiệm của phương trình 2x – 4 = 0 là S1 = {2}.
+) Ta có: (x – 2)(x2 + 1) = 0
Vì x2 ≥ 0 với mọi x ∈ ℝ nên x2 + 1 > 0 với mọi x ∈ ℝ.
Do đó, (x – 2)(x2 + 1) = 0 khi x – 2 = 0 hay x = 2.
Vậy tập nghiệm của phương trình (x – 2)(x2 + 1) = 0 là S2 = {2}.
+) Nhận thấy S1 = S2 = {2}. Vậy hai phương trình đã cho có cùng tập nghiệm.
Luyện tập 1 trang 32 Toán 11 Tập 1: Xét sự tương đương của hai phương trình sau:
và x2 – 1 = 0.
Lời giải:
+) Ta có: , điều kiện x ≠ – 1.
Khi đó, khi x – 1 = 0 hay x = 1 (thỏa mãn).
Vậy tập nghiệm của phương trình là S1 = {1}.
+) Phương trình x2 – 1 = 0 được viết lại thành (x – 1)(x + 1) = 0, từ đó ta tìm được x = 1 hoặc x = – 1, do đó tập nghiệm của phương trình x2 – 1 = 0 là S2 = {– 1; 1}.
+) Nhận thấy S1 ≠ S2, vậy hai phương trình đã cho không tương đương.
HĐ2 trang 32 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình sin x =
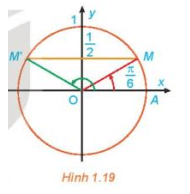
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
Lời giải:
a) Từ Hình 1.19, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc và , lại có tung độ của điểm M và M' đều bằng nên theo định nghĩa giá trị lượng giác, ta có và .
Vậy trong nửa khoảng [0; 2π), phương trình có hai nghiệm là , .
b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là và .
Luyện tập 2 trang 34 Toán 11 Tập 1: Giải các phương trình sau:
a) ;
b) sin 3x = – sin 5x.
Lời giải:
a)
Vậy phương trình có các nghiệm là và , .
b) sin 3x = – sin 5x
⇔ sin 3x = sin (– 5x)
Vậy phương trình đã cho có các nghiệm là và .
HĐ3 trang 34 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cos x =
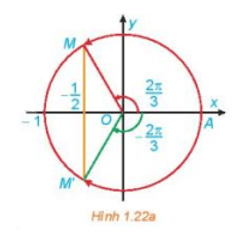
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [– π; π).
b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.
Lời giải:
a) Từ Hình 1.22a, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc và , lại có hoành độ của điểm M và M' đều bằng nên theo định nghĩa giá trị lượng giác, ta có và .
Vậy trong nửa khoảng [– π; π), phương trình có hai nghiệm là , .
b) Vì hàm số cos có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là và .
Luyện tập 3 trang 35 Toán 11 Tập 1: Giải các phương trình sau:
a) 2cos x = ;
b) cos 3x – sin 5x = 0.
Lời giải:
a) 2cos x =
Vậy phương trình đã cho có các nghiệm là và .
b) cos 3x – sin 5x = 0
⇔ cos 3x = sin 5x
Vậy phương trình đã cho có các nghiệm là và
.
(Theo trang usno.navy.mil).
Xác định góc α tương ứng với các pha sau của Mặt Trăng:
a) F = 0 (trăng mới);
b) F = 0,25 (trăng lưỡi liềm);
c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng);
d) F = 1 (trăng tròn).

Lời giải:
a) Với F = 0, ta có ⇔ cos α = 1 ⇔ α = k2π, k ∈ ℤ.
b) Với F = 0,25, ta có
.
c) Với F = 0,5, ta có ⇔ cos α = 0 ⇔ α = + kπ, k ∈ ℤ.
d) Với F = 1, ta có ⇔ cos α = – 1 ⇔ α = π + k2π, k ∈ ℤ.
HĐ4 trang 36 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình tan x = 1
a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại mấy điểm trên khoảng ?
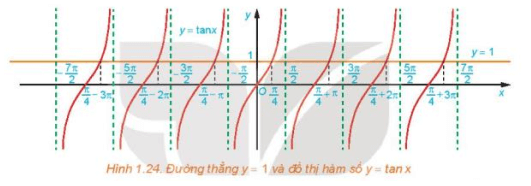
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho.
Lời giải:
a) Quan sát Hình 1.24, ta thấy trên khoảng , đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại 1 điểm, điểm này có hoành độ .
b) Từ câu a, ta suy ra phương trình tan x = 1 có nghiệm là trên khoảng .
Do hàm số tang có chu kì là π, nên công thức nghiệm của phương trình tan x = 1 là .
Luyện tập 4 trang 36 Toán 11 Tập 1: Giải các phương trình sau:
a) ;
b) tan 3x + tan 5x = 0.
Lời giải:
a)
Vậy phương trình đã cho có nghiệm là .
b) tan 3x + tan 5x = 0
⇔ tan 3x = – tan 5x
⇔ tan 3x = tan (– 5x)
⇔ 3x = – 5x + kπ, k ∈ ℤ
⇔ 8x = kπ, k ∈ ℤ
⇔ x =
Vậy phương trình đã cho có nghiệm là x =
HĐ5 trang 37 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cot x = – 1
a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại mấy điểm trên khoảng (0; π)?

b) Dựa vào tính tuần hoàn của hàm côtang, hãy viết công thức nghiệm của phương trình đã cho.
Lời giải:
a) Quan sát Hình 1.25, ta thấy trên khoảng (0; π), đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại 1 điểm, điểm này có hoành độ .
b) Từ câu a, ta suy ra phương trình cot x = – 1 có nghiệm là trên khoảng (0; π).
Do hàm số côtang có chu kì là π, nên công thức nghiệm của phương trình cot x = – 1 là
Luyện tập 5 trang 37 Toán 11 Tập 1: Giải các phương trình sau:
a) cot x = 1;
b) .
Lời giải:
a) cot x = 1
Vậy phương trình đã cho có nghiệm là .
b)
Vậy phương trình đã cho có nghiệm là .
a) cos α = – 0,75;
b) tan α = 2,46;
c) cot α = – 6,18.
Lời giải:
a) cos α = – 0,75
+ Để tìm số đo độ của góc α, ta bấm phím như sau:
Màn hình hiện kết quả là: 138°35'25,36''.
Vậy α ≈ 138°35'26".
+ Để tìm số đo rađian của góc α, ta bấm phím như sau:
Màn hình hiện kết quả là: 2,418858406.
Vậy α ≈ 2,41886 rad.
b) tan α = 2,46
+ Để tìm số đo độ của góc α, ta bấm phím như sau:
Màn hình hiện kết quả là: 67°52'41,01".
Vậy α ≈ 67°52'41".
+ Để tìm số đo rađian của góc α, ta bấm phím như sau:
Màn hình hiện kết quả là: 1,184695602.
Vậy α ≈ 1,1847 rad.
c) cot α = – 6,18
+ Để tìm số đo độ của góc α, ta bấm phím như sau:
Màn hình hiện kết quả là: – 9°11'29,38".
Vậy α ≈ – 9°11'30".
+ Để tìm số đo rađian của góc α, ta bấm phím như sau:
![]()
Màn hình hiện kết quả là: – 0,1604218219.
Vậy α ≈ – 0,16042 rad.
Bài tập
Bài 1.19 trang 39 Toán 11 Tập 1: Giải các phương trình sau:
a) ;
b) ;
c) ;
d) .
Lời giải:
a)
Vậy phương trình đã cho có các nghiệm là và .
b)
Vậy phương trình đã cho có các nghiệm là và .
c)
Vậy phương trình đã cho có nghiệm là x = 30° + k360°, k ∈ ℤ.
d)
Vậy phương trình đã cho có nghiệm là .
Bài 1.20 trang 39 Toán 11 Tập 1: Giải các phương trình sau:
a) sin 2x + cos 4x = 0;
b) cos 3x = – cos 7x.
Lời giải:
a) sin 2x + cos 4x = 0
⇔ cos 4x = – sin 2x
⇔ cos 4x = sin(– 2x)
⇔ cos 4x = cos
⇔ cos 4x = cos
Vậy phương trình đã cho có các nghiệm là và .
b) cos 3x = – cos 7x
⇔ cos 3x = cos(π + 7x)
Vậy phương trình đã cho có các nghiệm là và .
a) Tính theo góc bắn α tầm xa mà quả đạn đạt tới (tức là khoảng cách từ vị trí bắn đến điểm quả đạn chạm đất).
b) Tìm góc bắn α để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m.
c) Tìm góc bắn α để quả đạn đạt độ cao lớn nhất.
Lời giải:
Vì v0 = 500 m/s, g = 9,8 m/s2 nên ta có phương trình quỹ đạo của quả đạn là
hay .
a) Quả đạn chạm đất khi y = 0, khi đó
Loại x = 0 (đạn pháo chưa được bắn).
Vậy tầm xa mà quả đạn đạt tới là (m).
b) Để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m thì x = 22 000 m.
Khi đó ⇔ sin 2α =
Gọi là góc thỏa mãn . Khi đó ta có: sin 2α = sin β
.
c) Hàm số là một hàm số bậc hai có đồ thị là một parabol có tọa độ đỉnh I(xI; yI) là
Hay
Do đó, độ cao lớn nhất của quả đạn là .
Ta có , dấu “=” xảy ra khi sin2 α = 1 hay α = 90°.
Như vậy góc bắn α = 90° thì quả đan đạt độ cao lớn nhất.
Ở đây, thời gian t tính bằng giây và quãng đường x tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Lời giải:
Vị trí cân bằng của vật dao động điều hòa là vị trí vật đứng yên, khi đó x = 0, ta có
Trong khoảng thời gian từ 0 đến 6 giây, tức là 0 ≤ t ≤ 6 hay
Vì k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8}.
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.
Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.