Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 4: Phương trình lượng giác cơ bản sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 4.

SBT Toán 11 (Kết nối tri thức) Bài 4: Phương trình lượng giác cơ bản

Bài 1.25 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:

a) $2\sin \left(\frac{x}{3}+15°\right)+\sqrt{2}=0$ ;

b) $\cos \left(2x+\frac{\pi }{5}\right)=-1$ ;

c) 3tan 2x + $\sqrt{3}$  = 0;

d) cot (2x – 3) = cot 15°.

Lời giải:

a) $2\sin \left(\frac{x}{3}+15°\right)+\sqrt{2}=0$

$\iff \sin \left(\frac{x}{3}+15°\right)=-\frac{\sqrt{2}}{2}$

$\iff \sin \left(\frac{x}{3}+15°\right)=\sin \left(-45°\right)$

b) $\cos \left(2x+\frac{\pi }{5}\right)=-1$

$\iff 2x+\frac{\pi }{5}=\pi +k2\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\frac{2\pi }{5}+k\pi \left(k\in \mathbb{Z}\right)$.

c) 3tan 2x + $\sqrt{3}$  = 0

$\iff \tan 2x=-\frac{\sqrt{3}}{3}$

$\iff \tan 2x=\tan \left(-\frac{\pi }{6}\right)$

$\iff 2x=-\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff x=-\frac{\pi }{12}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$.

d) cot (2x – 3) = cot 15°

⇔ 2x – 3 = 15° + k180°  (k∈ ℤ)

⇔ 2x = 3 + 15° + k180°  (k∈ ℤ)

⇔ x = 1,5 + 7,5° + k90°  (k∈ ℤ).

Bài 1.26 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:

a) sin(2x + 15°) + cos(2x – 15°) = 0;

b) $\cos \left(2x+\frac{\pi }{5}\right)+\cos \left(3x-\frac{\pi }{6}\right)=0$ ;

c) tan x + cot x = 0;

d) sin x + tan x = 0.

Lời giải:

a) Ta có sin(2x + 15°) + cos(2x – 15°) = 0

⇔ sin(2x + 15°) = – cos(2x – 15°)

⇔ sin(2x + 15°) = – sin[90° – (2x – 15°)]

⇔ sin(2x + 15°) = sin[– 90° + (2x – 15°)]

⇔ sin(2x + 15°) = sin(2x – 105°)

Không xảy ra trường hợp 120° = k360°.

Vậy phương trình đã cho có nghiệm x = 67,5° + k90° (k ∈ ℤ). 

b)$\cos \left(2x+\frac{\pi }{5}\right)+\cos \left(3x-\frac{\pi }{6}\right)=0$

$\iff \cos \left(2x+\frac{\pi }{5}\right)=\cos \left(\frac{7\pi }{6}-3x\right)$

c) Ta có tan x + cot x = 0

⇔ tan x = – cot x

⇔ tan x = cot(π – x)

$\iff \tan x=\tan \left(x-\frac{\pi }{2}\right)$

$\iff x=x-\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff \frac{\pi }{2}-k\pi =0\left(k\in \mathbb{Z}\right)$. Vô lí.

Vậy phương trình đã cho vô nghiệm.

d) Điều kiện cos x ≠ 0 .

Ta có sin x + tan x = 0

$\iff \sin x+\frac{\sin x}{\cos x}=0$

$\iff \sin x\left(1+\frac{1}{\cos x}\right)=0$

⇔ sin x = 0  (do sin² x + cos² x = 1)

⇔ x = kπ (k ∈ ℤ).

Vì x = kπ (k ∈ ℤ) thoả mãn điều kiện cos x ≠ 0 nên nghiệm của phương trình đã cho là

x = kπ (k ∈ ℤ).

Bài 1.27 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:

a) (2 + cos x)(3cos 2x – 1) = 0;

b) 2sin 2x – sin 4x = 0;

c) cos⁶ x – sin⁶ x = 0;

d) tan 2x cot x = 1. 

Lời giải:

a) Ta có (2 + cos x)(3cos 2x – 1) = 0

+ Phương trình 2 + cos x = 0 vô nghiệm vì – 1 ≤ cos x ≤ 1.

+ Gọi α là góc thoả mãn cos α = $\frac{1}{3}$ . Ta có

3cos 2x – 1 = 0 ⇔ cos 2x = cos α ⇔ 2x = ± α + k2π (k ∈ ℤ) ⇔ x = $\pm \frac{\alpha }{2}$  + kπ (k ∈ ℤ).

Vậy nghiệm của phương trình đã cho là x = $\pm \frac{\alpha }{2}$  + kπ (k ∈ ℤ) với cos α = $\frac{1}{3}$ .

b) Ta có 2sin 2x – sin 4x = 0

⇔ 2sin 2x – 2sin 2x cos 2x = 0

⇔ 2sin 2x(1 – cos2x) = 0

Do sin² 2x + cos² 2x = 1 nên cos 2x = 1 kéo theo sin 2x = 0, do đó phương trình đã cho tương đương với

sin 2x = 0 ⇔ 2x = kπ (k ∈ ℤ) $\iff x=k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

c) Ta có cos⁶ x – sin⁶ x = 0

⇔ cos⁶ x = sin⁶ x

⇔ (cos² x)³ = (sin² x)³

⇔ cos² x = sin² x

⇔ cos² x – sin² x = 0

⇔ cos 2x = 0

Từ đó ta được 2x = $\frac{\pi }{2}$  + kπ (k ∈ ℤ) hay $x=\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

d) Điều kiện sin x ≠ 0 và cos 2x ≠ 0.

Ta có tan 2x cot x = 1

$\iff \tan 2x=\frac{1}{\cot x}$

⇔ tan 2x = tan x

⇔ 2x = x + kπ   (k ∈ ℤ)

⇔ x = kπ   (k ∈ ℤ).

Ta thấy x = kπ (k ∈ ℤ) không thoả mãn điều kiện sin x ≠ 0.

Vậy phương trình đã cho vô nghiệm.

Bài 1.28 trang 24 SBT Toán 11 Tập 1: Tìm các giá trị của x để giá trị tương ứng của các hàm số sau bằng nhau:

a) $y=\cos \left(2x-\frac{\pi }{3}\right)$  và $y=\cos \left(x-\frac{\pi }{4}\right)$ ;

b)  $y=\sin \left(3x-\frac{\pi }{4}\right)$và $y=\sin \left(x-\frac{\pi }{6}\right)$ .

Lời giải:

a) Giá trị tương ứng của hai hàm số $y=\cos \left(2x-\frac{\pi }{3}\right)$  và $y=\cos \left(x-\frac{\pi }{4}\right)$  bằng nhau nếu $\cos \left(2x-\frac{\pi }{3}\right)=\cos \left(x-\frac{\pi }{4}\right)$

b) Giá trị tương ứng của hai hàm số $y=\sin \left(3x-\frac{\pi }{4}\right)$  và $y=\sin \left(x-\frac{\pi }{6}\right)$  bằng nhau nếu $\sin \left(3x-\frac{\pi }{4}\right)=\sin \left(x-\frac{\pi }{6}\right)$

Bài 1.29 trang 24 SBT Toán 11 Tập 1: Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là h = |y| trong đó

$y=2+\mathrm{2,5}\sin 2\pi \left(x-\frac{1}{4}\right)$

với x là thời gian quay của guồng (x ≥ 0), tính bằng phút; ta quy ước rằng y > 0 khi gầu ở trên mặt nước và y < 0 khi gầu ở dưới mặt nước.

a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?

b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?

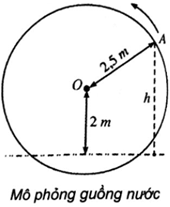
Lời giải:

a) Vì $-1\le \sin 2\pi \left(x-\frac{1}{4}\right)\le 1$  nên $-\mathrm{2,5}\le \mathrm{2,5}\sin 2\pi \left(x-\frac{1}{4}\right)\le \mathrm{2,5}$  và do đó ta có $2-\mathrm{2,5}\le 2+\mathrm{2,5}\sin 2\pi \left(x-\frac{1}{4}\right)\le 2+\mathrm{2,5}$

hay $-\mathrm{0,5}\le 2+\mathrm{2,5}\sin 2\pi \left(x-\frac{1}{4}\right)\le \mathrm{4,5}\forall x\in ℝ$ .

Suy ra, gầu ở vị trí cao nhất khi $\sin 2\pi \left(x-\frac{1}{4}\right)=1$ $\iff 2\pi \left(x-\frac{1}{4}\right)=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\frac{1}{2}+k\left(k\in \mathbb{Z}\right)$. Do x ≥ 0 nên $x=\frac{1}{2}+k\left(k\in \mathbb{N}\right)$ .

Vậy gầu ở vị trí cao nhất tại các thời điểm $\frac{1}{2},\frac{3}{2},\frac{5}{2}\mathrm{,...}$  phút.

Tương tự, gầu ở vị trí thấp nhất khi $\sin 2\pi \left(x-\frac{1}{4}\right)=-1$

$\iff 2\pi \left(x-\frac{1}{4}\right)=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

$\iff x=k\left(k\in \mathbb{Z}\right)$. Do x ≥ 0 nên $x=k\left(k\in \mathbb{N}\right)$ .

Vậy gàu ở vị trí thấp nhất tại các thời điểm 0, 1, 2, 3, ... phút.

b) Gầu cách mặt nước 2 m khi $2+\mathrm{2,5}\sin 2\pi \left(x-\frac{1}{4}\right)=2$

$\iff \sin 2\pi \left(x-\frac{1}{4}\right)=0$

$\iff 2\pi \left(x-\frac{1}{4}\right)=k\pi \left(k\in \mathbb{Z}\right)$

$\iff x=\frac{1}{4}+\frac{k}{2}\left(k\in \mathbb{Z}\right)$

Do x ≥ 0 nên $x=\frac{1}{4}+\frac{k}{2}\left(k\in \mathbb{N}\right)$ .

Vậy chiếc gầu cách mặt nước 2 m lần đầu tiên tại thời điểm $x=\frac{1}{4}$  phút.

Bài 1.30 trang 25 SBT Toán 11 Tập 1: Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t (ở đây t là số ngày tính từ ngày 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số

$L\left(t\right)=12+\mathrm{2,83}\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)$ với t ∈ ℤ và 0 < t ≤ 365.

a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?

b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?

c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?

Lời giải:

Vì $-1\le \sin \left(\frac{2\pi }{365}\left(t-80\right)\right)\le 1$  nên $-\mathrm{2,83}\le \mathrm{2,83}\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)\le \mathrm{2,83}$ , do đó $12-\mathrm{2,83}\le 12+\mathrm{2,83}\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)\le 12+\mathrm{2,83}$

hay $\mathrm{9,17}\le 12+\mathrm{2,83}\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)\le \mathrm{14,83}\forall t\in ℝ$ .

a) Ngày thành phố A có ít giờ ánh sáng mặt trời nhất ứng với

$\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)=-1$

$\iff \frac{2\pi }{365}\left(t-80\right)=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

$\iff t=-\frac{45}{4}+365k\left(k\in \mathbb{Z}\right)$

Vì 0 < t ≤ 365 nên k = 1 suy ra t = $-\frac{45}{4}$  + 365 = 353,75.

Như vậy, vào ngày thứ 353 của năm, tức là khoảng ngày 20 tháng 12 thì thành phố A sẽ có ít giờ ánh sáng mặt trời nhất.

b) Ngày thành phố A có nhiều giờ ánh sáng mặt trời nhất ứng với  

$\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)=1$

$\iff \frac{2\pi }{365}\left(t-80\right)=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$

$\iff t=\frac{685}{4}+365k\left(k\in \mathbb{Z}\right)$

Vì 0 < t ≤ 365 nên k = 0 suy ra t = $\frac{685}{4}$  = 171,25.

Như vậy, vào ngày thứ 171 của năm, tức là khoảng ngày 20 tháng 6 thì thành phố A sẽ có nhiều giờ ánh sáng mặt trời nhất.

c) Thành phố A có khoảng 10 giờ ánh sáng mặt trời trong ngày nếu

 $12+\mathrm{2,83}\sin \left(\frac{2\pi }{365}\left(t-80\right)\right)=10$

$\iff \sin \left(\frac{2\pi }{365}\left(t-80\right)\right)=-\frac{200}{283}$

Từ đó ta được  .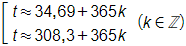

Vì 0 < t ≤ 365 nên k = 0 suy ra t ≈ 34,69 hoặc t ≈ 308,3.

Như vậy, vào khoảng ngày thứ 34 của năm, tức là ngày 3 tháng 2 và ngày thứ 308 của năm, tức là ngày 4 tháng 11 thành phố A sẽ có 10 giờ ánh sáng mặt trời.

Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 3: Hàm số lượng giác

Bài tập cuối chương 1 trang 25

Bài 5: Dãy số

Bài 6: Cấp số cộng

Bài 7: Cấp số nhân