Với giải SGK Toán 11 Kết nối tri thức trang 32 chi tiết trong Bài 4: Phương trình lượng giác cơ bản giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 32 Tập 1 (Kết nối tri thức)
Luyện tập 1 trang 32 Toán 11 Tập 1: Xét sự tương đương của hai phương trình sau:
và x2 – 1 = 0.
Lời giải:
+) Ta có: , điều kiện x ≠ – 1.
Khi đó, khi x – 1 = 0 hay x = 1 (thỏa mãn).
Vậy tập nghiệm của phương trình là S1 = {1}.
+) Phương trình x2 – 1 = 0 được viết lại thành (x – 1)(x + 1) = 0, từ đó ta tìm được x = 1 hoặc x = – 1, do đó tập nghiệm của phương trình x2 – 1 = 0 là S2 = {– 1; 1}.
+) Nhận thấy S1 ≠ S2, vậy hai phương trình đã cho không tương đương.
HĐ2 trang 32 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình sin x =
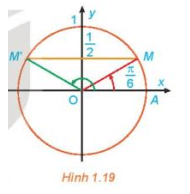
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
Lời giải:
a) Từ Hình 1.19, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc và , lại có tung độ của điểm M và M' đều bằng nên theo định nghĩa giá trị lượng giác, ta có và .
Vậy trong nửa khoảng [0; 2π), phương trình có hai nghiệm là , .
b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là và .
Xem thêm các bài giải Toán 11 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 31 Toán 11 Tập 1: Nhận biết khái niệm hai phương trình tương đương
Luyện tập 1 trang 32 Toán 11 Tập 1: Xét sự tương đương của hai phương trình sau:
HĐ2 trang 32 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình sin x =
Luyện tập 2 trang 34 Toán 11 Tập 1: Giải các phương trình sau:
HĐ3 trang 34 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cos x =
Luyện tập 3 trang 35 Toán 11 Tập 1: Giải các phương trình sau:
HĐ4 trang 36 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình tan x = 1
HĐ5 trang 37 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cot x = – 1
Luyện tập 5 trang 37 Toán 11 Tập 1: Giải các phương trình sau:
Bài 1.19 trang 39 Toán 11 Tập 1: Giải các phương trình sau:
Bài 1.20 trang 39 Toán 11 Tập 1: Giải các phương trình sau:
Xem thêm các bài giải Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.