Với giải Khám phá 1 trang 18 Toán 8 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3: Hằng đẳng thức đáng nhớ giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Khám phá 1 trang 18 Toán 8 Tập 1 | Chân trời sáng tạo Giải Toán lớp 8
Khám phá 1 trang 18 Toán 8 Tập 1: a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1 như sau:
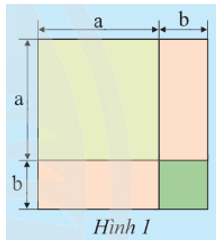
An: S = (a + b)2.
Mai: S = a2 + b2 + ab + ba.
Bình: S = a2 + 2ab + b2.
Kết quả của mỗi bạn có đúng không? Giải thích.
b) Thực hiện phép nhân và rút gọn đa thức của bạn An.
c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức (a − b)2 thành biểu thức nào?
Lời giải:
a) Ta xét các cách tính diện tích của các phần tô màu trong Hình 1 như sau:
Cách 1: Tính diện tích của hình vuông được ghép bởi 4 hình:
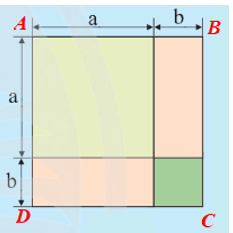
Cạnh của hình vuông ABCD được tạo thành là: a + b.
Diện tích S của các phần tô màu chính là diện tích của hình vuông ABCD, và bằng:
S = (a + b)2 .
Do đó kết quả của bạn An là đúng.
Cách 2: Tính diện tích mỗi hình:
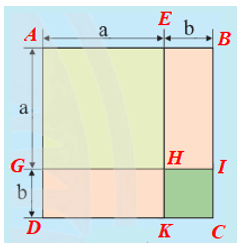
Diện tích hình vuông màu vàng AEHG là: a2.
Diện tích hình vuông màu xanh HICK là: b2.
Diện tích hình chữ nhật màu hồng EBIH là: ab.
Diện tích hình chữ nhật màu hồng GHKD là: ba.
Diện tích S của các phần tô màu là: a2 + b2 + ab + ba.
Do đó kết quả của bạn Mai là đúng.
Cách 3: Tính tổng diện tích hai hình chữ nhật ABIG và GICD (hình vẽ dưới đây).
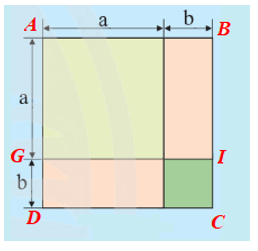
Diện tích hình chữ nhật ABIG là: a.(a + b) = a.a + a.b = a2 + ab.
Diện tích hình chữ nhật GICD là: (a + b).b = a.b + b.b = ab + b2.
Diện tích S của các phần tô màu là: a2 + ab + ab + b2 = a2 + 2ab + b2.
Vậy kết quả của bạn Bình là đúng.
Lưu ý: Có nhiều cách tính diện tích S của các phần tô màu để khẳng định kết quả của cả ba bạn đều đúng.
b) Ta có: S = (a + b)2
= (a + b).(a + b)
= a.(a + b) + b.(a + b)
= a.a + a.b + b.a + b.b
= a2 + 2ab + b2.
c) Ta có: (a – b)2
= (a – b).(a – b)
= a.(a – b) – b.(a – b)
= a.a – a.b – b.a + b.b
= a2 – 2ab + b2.
Xem thêm các bài giải Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Khởi động trang 18 Toán 8 Tập 1: Hãy tính nhanh 652 – 352 = ?; 102 . 98 = ?
Thực hành 1 trang 19 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức a) (3x + 1)2; b) (4x + 5y)2;
Thực hành 3 trang 19 Toán 8 Tập 1: Tính nhanh 52^2; 982.
Thực hành 5 trang 20 Toán 8 Tập 1: Tính nhanh 82 . 78; 87 . 93; 1252 – 252.
Vận dụng 2 trang 20 Toán 8 Tập 1: Giải đáp câu hỏi ở Hoạt động khởi động (trang 18)
Thực hành 6 trang 21 Toán 8 Tập 1: Tính a) (x + 2y)3;
Thực hành 7 trang 21 Toán 8 Tập 1: Viết các đa thức sau dưới dạng tích
Thực hành 8 trang 21 Toán 8 Tập 1: Tính (x + 1)(x2 – x + 1);
Bài 1 trang 22 Toán 8 Tập 1: Tính (3x + 4)2;
Bài 2 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu
Bài 3 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức
Bài 5 trang 22 Toán 8 Tập 1: Tính nhanh 38 . 42; 1022;
Bài 6 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức (2x – 3)3; (a + 3b)3; (xy –1)3.
Bài 7 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức (a – 5)(a2 + 5a + 25); (x + 2y)(x2 – 2xy + 4y2).
Bài 8 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức: (a – 1)(a + 1)(a2 + 1); (xy + 1)2 – (xy – 1)2.
Bài 9 trang 22 Toán 8 Tập 1: a) Cho x + y = 12 và xy = 35. Tính (x − y)2.
Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Đơn thức và đa thức nhiều biến
Bài 2: Các phép toán với đa thức nhiều biến
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.