Toptailieu biên soạn và giới thiệu lời giải Toán 8 Bài 3 (Chân trời sáng tạo): Hằng đẳng thức đáng nhớ hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 8 Bài 3 từ đó học tốt môn Toán 8.

Toán 8 (Chân trời sáng tạo) Bài 3: Hằng đẳng thức đáng nhớ

Giải Toán 8 trang 18 Tập 1

Khởi động trang 18 Toán 8 Tập 1: Hãy tính nhanh:

65² – 35² = ?

102 . 98 = ?

Bạn nữ: “Đáp số là 3 000 và 9 996”.

Bạn nam: “Trời! Bạn làm thế nào mà nhanh vậy?”

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

65² – 35² = (65 + 35) . (65 – 35) = 100 . 30 = 3 000.

102 . 98 = (100 + 2) . (100 – 2) = 100² – 2² = 10 000 – 4 = 9 996.

1. Bình phương của một tổng, một hiệu

Khám phá 1 trang 18 Toán 8 Tập 1: a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1 như sau:

An: S = (a + b)².

Mai: S = a² + b² + ab + ba.

Bình: S = a² + 2ab + b².

Kết quả của mỗi bạn có đúng không? Giải thích.

b) Thực hiện phép nhân và rút gọn đa thức của bạn An.

c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức (a − b)² thành biểu thức nào?

Lời giải:

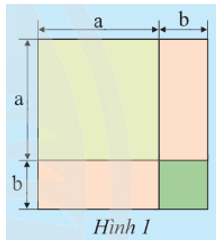
a) Ta xét các cách tính diện tích của các phần tô màu trong Hình 1 như sau:

Cách 1: Tính diện tích của hình vuông được ghép bởi 4 hình:

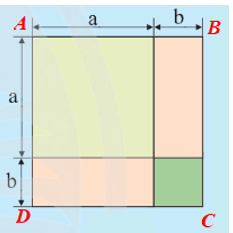
Cạnh của hình vuông ABCD được tạo thành là: a + b.

Diện tích S của các phần tô màu chính là diện tích của hình vuông ABCD, và bằng:

S = (a + b)² .

Do đó kết quả của bạn An là đúng.

Cách 2: Tính diện tích mỗi hình:

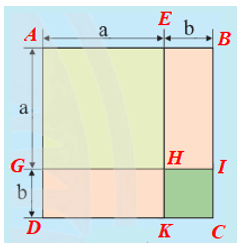
Diện tích hình vuông màu vàng AEHG là: a².

Diện tích hình vuông màu xanh HICK là: b².

Diện tích hình chữ nhật màu hồng EBIH là: ab.

Diện tích hình chữ nhật màu hồng GHKD là: ba.

Diện tích S của các phần tô màu là: a² + b² + ab + ba.

Do đó kết quả của bạn Mai là đúng.

Cách 3: Tính tổng diện tích hai hình chữ nhật ABIG và GICD (hình vẽ dưới đây).

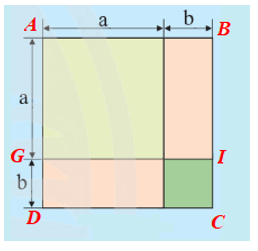
Diện tích hình chữ nhật ABIG là: a.(a + b) = a.a + a.b = a² + ab.

Diện tích hình chữ nhật GICD là: (a + b).b = a.b + b.b = ab + b².

Diện tích S của các phần tô màu là: a² + ab + ab + b² = a² + 2ab + b².

Vậy kết quả của bạn Bình là đúng.

Lưu ý: Có nhiều cách tính diện tích S của các phần tô màu để khẳng định kết quả của cả ba bạn đều đúng.

b) Ta có: S = (a + b)²

                  = (a + b).(a + b)

                  = a.(a + b) + b.(a + b)

                  = a.a + a.b + b.a + b.b

                  = a² + 2ab + b².

c) Ta có: (a – b)²

            = (a – b).(a – b)

            = a.(a – b) – b.(a – b)

            = a.a – a.b – b.a + b.b

            = a² – 2ab + b².

Giải Toán 8 trang 19 Tập 1

Thực hành 1 trang 19 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (3x + 1)²;

b) (4x + 5y)²;

c) ${\left(5x-\frac{1}{2}\right)}^2$;

d) (–x + 2y²)².

Lời giải:

a) (3x + 1)²

= (3x)² + 2.3x.1 + 1²

= 9x² + 6x + 1.

b) (4x + 5y)²

= (4x)² + 2.4x.5y + (5y)²

= 16x² + 40xy + 25y².

c) ${\left(5x-\frac{1}{2}\right)}^2$

$={\left(5x\right)}^2+2.5x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2$

$=25x^2+5x+\frac{1}{4}$.

d) (–x + 2y²)²

= (–x)² + 2.(–x).2y² + (2y²)²

= x² – 4xy² + 4y⁴.

Thực hành 2 trang 19 Toán 8 Tập 1: Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) a² + 10ab + 25b²;

b) 1 + 9a² – 6a.

Lời giải:

a) a² + 10ab + 25b²

= a² + 2.a.5b + (5b)²

= (a + 5b)².

b) 1 + 9a² – 6a

= 1 – 6a + 9a²

= 1² – 2.1.3a + (3a)²

= (1 – 3a)².

Hoặc ta có thể viết như sau:

1 + 9a² – 6a

= 9a² – 6a + 1

= (3a)² – 2.3a.1 + 1²

= (3a – 1)².

Thực hành 3 trang 19 Toán 8 Tập 1: Tính nhanh:

a) 52²;

b) 98².

Lời giải:

a) 52² = (50 + 2)² = 50² + 2.50.2 + 2² = 2 500 + 200 + 4 = 2 704.

b) 98² = (100 – 2)² = 100² – 2.100.2 + 2² = 10 000 – 400 + 4 = 9 604.

Vận dụng 1 trang 19 Toán 8 Tập 1:

a) Một mảnh vườn hình vuông có cạnh 10 m được mở rộng cả hai cạnh thêm x (m) như Hình 2a. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn sau khi mở rộng.

b) Một mảnh vườn hình vuông sau khi mở rộng mỗi cạnh 5 m thì được một mảnh vườn hình vuông với cạnh là x (m) như Hình 2b. Viết biểu thức (dạng đa thức thu gọn) biểu thị diện tích mảnh vườn trước khi mở rộng.

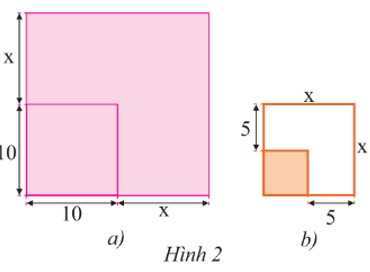
Lời giải:

a) Mảnh vườn hình vuông có cạnh 10 m được mở rộng cả hai cạnh thêm x (m) nên mảnh vườn lúc này có dạng hình vuông với độ dài cạnh là 10 + x (m).

Diện tích mảnh vườn sau khi mở rộng là:

(10 + x)² = 10² + 2.10.x + x² = 100 + 20x + x² (m²).

Vậy biểu thức biểu thị diện tích mảnh vườn sau khi mở rộng là 100 + 20x + x² (m²).

b) Mảnh vườn hình vuông trước khi mở rộng có độ dài cạnh là: x – 5 (m).

Diện tích mảnh vườn hình vuông trước khi mở rộng là:

(x – 5)² = x² – 2.x.5 + 5² = x² – 10x + 25 (m²).

Vậy biểu thức biểu thị diện tích mảnh vườn trước khi mở rộng là x² – 10x + 25 (m²).

Giải Toán 8 trang 20 Tập 1

2. Hiệu của hai bình phương

Khám phá 2 trang 20 Toán 8 Tập 1: a) Từ Hình 3a, người ta cắt ghép tạo thành Hình 3b. Viết hai biểu thức khác nhau, mỗi biểu thức biểu thị diện tích (phần tô màu) của một trong hai hình bên.

b) Thực hiện phép nhân và rút gọn đa thức, biến đổi biểu thức (a + b)(a – b) thành một đa thức thu gọn. Từ đó, có kết luận gì về diện tích của hai hình bên?

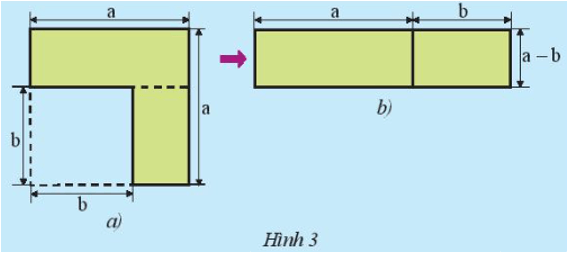
Lời giải:

a) Ta đặt tên các điểm trên Hình 3 như hình vẽ dưới đây.

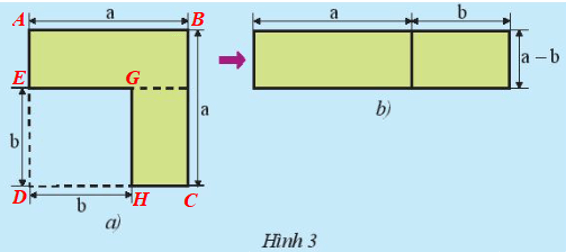
• Diện tích hình vuông ABCD là: a².

Diện tích hình vuông EGHD là: b².

Diện tích phần tô màu ở Hình 3a là: a² – b².

• Chiều dài của hình chữ nhật trong Hình 3b là: a + b.

Chiều rộng của hình chữ nhật trong Hình 3b là: a – b.

Diện tích hình chữ nhật (phần tô màu) trong Hình 3b là: (a + b)(a – b).

b) Ta có:

(a + b)(a – b) = a.(a – b) + b.(a – b) = a.a – ab + ba – b.b = a² – b².

Vậy diện tích của hai hình trong Hình 3a và Hình 3b trùng nhau.

Thực hành 4 trang 20 Toán 8 Tập 1: Thực hiện các phép nhân:

a) (4 – x)(4 + x);

b) (2y + 7z)(2y – 7z);

c) (x + 2y²)(x – 2y²).

Lời giải:

a) (4 – x).(4 + x) = 4² – x² = 16 – x².

b) (2y + 7z).(2y – 7z) = (2y)² – (7z)² = 4y² – 49z².

c) (x + 2y²).(x – 2y²) = x² – (2y²)² = x² – 4y⁴.

Thực hành 5 trang 20 Toán 8 Tập 1: Tính nhanh:

a) 82 . 78;

b) 87 . 93;

c) 125² – 25².

Lời giải:

a) 82 . 78 = (80 + 2).(80 – 2) = 80² – 2² = 6 400 – 4 = 6 396.

b) 87 . 93 = (90 – 3).(90 + 3) = 90² – 3² = 8 100 – 9 = 8 091.

c) 125² – 25² = (125 + 25).(125 – 25) = 150 . 100 = 15 000.

Vận dụng 2 trang 20 Toán 8 Tập 1: Giải đáp câu hỏi ở Hoạt động khởi động (trang 18).

Lời giải:

Ta tính nhanh các phép tính như sau:

65² – 35² = (65 + 35) . (65 – 35) = 100 . 30 = 3 000.

102 . 98 = (100 + 2) . (100 – 2) = 100² – 2² = 10 000 – 4 = 9 996.

3. Lập phương của một tổng, một hiệu

Khám phá 3 trang 20 Toán 8 Tập 1: Hoàn thành các phép nhân đa thức sau vào vở, thu gọn kết quả nhận được:

(a + b)³ = (a + b)(a + b)²

             = (a + b)(…)

             = …

(a – b)³ = (a – b)(a – b)²

             = (a – b)(…)

             = …

Lời giải:

(a + b)³ = (a + b)(a + b)²

             = (a + b)(a² + 2ab + b²)

             = a(a² + 2ab + b²) + b(a² + 2ab + b²)

             = a.a² + a.2ab + a.b² + b.a² + b.2ab + b.b²

             = a³ + 2a²b + ab² + a²b + 2ab² + b³

             = a³ + (2a²b + a²b) + (ab² + 2ab²) + b³

             = a³ + 3a²b + 3ab² + b³.

(a – b)³ = (a – b)(a – b)²

             = (a – b)(a² – 2ab + b²)

             = a(a² – 2ab + b²) – b(a² – 2ab + b²)

             = a.a² – a.2ab + a.b² – b.a² + b.2ab – b.b²

             = a³ – 2a²b + ab² – a²b + 2ab² – b³

             = a³ – (2a²b + a²b) + (ab² + 2ab²) – b³

             = a³ – 3a²b + 3ab² – b³.

Giải Toán 8 trang 21 Tập 1

Thực hành 6 trang 21 Toán 8 Tập 1: Tính:

a) (x + 2y)³;

b) (3y – 1)³.

Lời giải:

a) (x + 2y)³

= x³ + 3.x².2y + 3.x.(2y)² + (2y)³

= x³ + 6x²y + 12xy² + 8y³.

b) (3y – 1)³

= (3y)³ – 3.(3y)².1 + 3.3y.1² – 1³

= 27y³ – 27y² + 9y – 1.

Vận dụng 3 trang 21 Toán 8 Tập 1: Một thùng chứa dạng hình lập phương có độ dài cạnh bằng x (cm). Phần vỏ bao gồm nắp có độ dày 3 cm. Tính dung tích (sức chứa) của thùng, viết kết quả dưới dạng đa thức.

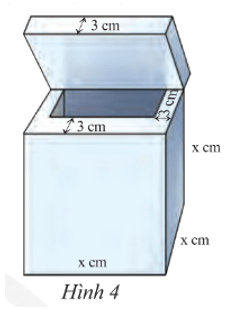
Lời giải:

Phần lòng trong của thùng chứa có dạnh hình lập phương với độ dài cạnh là x – 3 – 3 = x – 6 (cm).

Thể tích phần lòng trong của thùng là:

(x – 6)³ = x³ – 3.x².6 + 3.x.6² – 6³

             = x³ – 18x² + 108x – 216 (cm³).

Vậy dung tích (sức chứa) của thùng là x³ – 18x² + 108x – 216 (cm³).

4. Tổng và hiệu của hai lập phương

Khám phá 4 trang 21 Toán 8 Tập 1: Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở:

(a + b)³ = a³ + 3a²b + 3ab² + b³

a³ + b³ = (a + b)³ – 3a²b – 3ab²

           = (a + b)³ – 3ab(a + b)

           = (a + b)(…)

           = …

(a – b)³ = a³ – 3a²b + 3ab² – b³

a³ – b³ = (a – b)³ + 3a²b – 3ab²

           = (a – b)³ + 3ab(a – b)

           = (a – b)(…)

           = …

Lời giải:

(a + b)³ = a³ + 3a²b + 3ab² + b³

a³ + b³ = (a + b)³ – 3a²b – 3ab²

           = (a + b)³ – 3ab(a + b)

           = (a + b)[(a + b)² – 3ab]

           = (a + b)(a² + 2ab + b² – 3ab)

           = (a + b)(a² – ab + b²).

(a – b)³ = a³ – 3a²b + 3ab² – b³

a³ – b³ = (a – b)³ + 3a²b – 3ab²

           = (a – b)³ + 3ab(a – b)

           = (a – b)[(a – b)² + 3ab]

           = (a – b)(a² – 2ab + b² + 3ab)

           = (a – b)(a² + ab + b²).

Thực hành 7 trang 21 Toán 8 Tập 1: Viết các đa thức sau dưới dạng tích:

a) 8y³ + 1;

b) y³ – 8.

Lời giải:

a) 8y³ + 1 = (2y)³ + 1

                = (2y + 1)[(2y)² – 2y.1 + 1²]

                = (2y + 1)(4y² – 2y + 1)

b) y³ – 8 = y³ – 2³

              = (y – 2)(y² + y.2 + 2²)

              = (y – 2)(y² + 2y + 4).

Thực hành 8 trang 21 Toán 8 Tập 1: Tính:

a) (x + 1)(x² – x + 1);

b) $\left(2x-\frac{1}{2}\right)\left(4x^2+1+\frac{1}{4}\right)$.

Lời giải:

a) (x + 1)(x² – x + 1)

= x³ + 1³

= x³ + 1.

b) $\left(2x-\frac{1}{2}\right)\left(4x^2+1+\frac{1}{4}\right)$.

$=\left(2x-\frac{1}{2}\right)\left[{\left(2x\right)}^2+2x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2\right]$

$={\left(2x\right)}^3-{\left(\frac{1}{2}\right)}^3$

$=8x^3-\frac{1}{8}$.

Giải Toán 8 trang 22 Tập 1

Vận dụng 4 trang 22 Toán 8 Tập 1: Từ một khối lập phương có cạnh bằng 2x + 1, ta cắt bỏ một khối lập phương có cạnh bằng x + 1 (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.

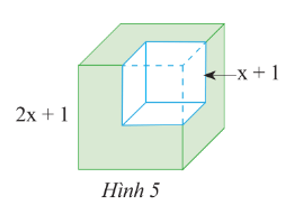
Lời giải:

Thể tích của khối lập phương có cạnh bằng 2x + 1 là: (2x + 1)³.

Thể tích của khối lập phương có cạnh bằng x + 1 là: (x + 1)³.

Cách 1: Thể tích phần còn lại là:

(2x + 1)³ – (x + 1)³

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³ – (x³ + 3.x².1 + 3.x.1² + 1³)

= 8x³ + 12x² + 6x + 1 – x³ – 3x² – 3x – 1

= (8x³ –  x³) + (12x² – 3x²) + (6x – 3x) + (1 – 1)

= 7x³ + 9x² + 3x.

Cách 1: Thể tích phần còn lại là:

(2x + 1)³ – (x + 1)³

= [(2x + 1) – (x + 1)].[(2x + 1)² + (2x + 1).(x + 1) + (x + 1)²]

= [2x + 1 – x – 1].[(2x)² + 2.2x.1 + 1² + (2x.x + 2x.x + 1.x + 1.1) + x² + 2.x.1 + 1²]

= x.[4x² + 4x + 1 + 2x² + 3x + 1 + x² + 2x + 1]

= x.[(4x² + 2x² + x²) + (4x + 3x + 2x) + (1 + 1 + 1)]

= x.[7x² + 9x + 3]

= 7x³ + 9x² + 3x.

Bài tập

Bài 1 trang 22 Toán 8 Tập 1: Tính:

a) (3x + 4)²;

b) (5x – y)²;

c) ${\left(xy-\frac{1}{2}y\right)}^2$.

Lời giải:

a) (3x + 4)²

= (3x)² + 2.3x.4 + 4²

= 9x² + 24x + 16.

b) (5x – y)²

= (5x)² – 2.5x.y + y²

= 25x² – 10xy + y².

c) ${\left(xy-\frac{1}{2}y\right)}^2$

$={\left(xy\right)}^2-2.xy.\frac{1}{2}y+{\left(\frac{1}{2}y\right)}^2$

$=x^2{y}^2-x{y}^2+\frac{1}{4}{y}^2$.

Bài 2 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) x² + 2x + 1;

b) 9 – 24x + 16x²;

c) 4x² + $\frac{1}{4}$ + 2x.

Lời giải:

a) x² + 2x + 1

= x² + 2.x.1 + 1²

= (x + 1)².

b) 9 – 24x + 16x²

= 3² – 2.3.4x + (4x)²

= (3 – 4x)².

Ta cũng có thể viết như sau:

9 – 24x + 16x²

= 16x² – 24x + 9

= (4x)² – 2.4x.3 + 3²

= (4x – 3)².

c) $4x^2+\frac{1}{4}+2x$

$=4x^2+2x+\frac{1}{4}$

$={\left(2x\right)}^2+2.2x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2$

$={\left(2x+\frac{1}{2}\right)}^2$.

Bài 3 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (3x – 5)(3x + 5);

b) (x – 2y)(x + 2y);

c) $\left(-x-\frac{1}{2}y\right)\left(-x+\frac{1}{2}y\right)$.

Lời giải:

a) (3x – 5)(3x + 5)

= (3x)² – 5²

= 9x² – 25.

b) (x – 2y)(x + 2y)

= x² – (2y)²

= x² – 4y².

c) $\left(-x-\frac{1}{2}y\right)\left(-x+\frac{1}{2}y\right)$

$={\left(-x\right)}^2-{\left(\frac{1}{2}y\right)}^2$

$=x^2-\frac{1}{4}{y}^2$.

Bài 4 trang 22 Toán 8 Tập 1: a) Viết biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 dưới dạng đa thức.

b) Viết biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 dưới dạng đa thức.

Lời giải:

a) Biểu thức tính diện tích của hình vuông có cạnh bằng 2x + 3 là:

(2x + 3)² = (2x)² + 2.2x.3 + 3² = 4x² + 12x + 9.

b) Biểu thức tính thể tích của khối lập phương có cạnh bằng 3x − 2 là:

(3x – 2)³ = (3x)³ – 3.(3x)².2 + 3.3x.2² – 2³

               = 27x³ – 54x² + 36x – 8.

Bài 5 trang 22 Toán 8 Tập 1: Tính nhanh:

a) 38 . 42;

b) 102²;

c) 198²;

d) 75² – 25².

Lời giải:

a) 38 . 42 = (40 – 2).(40 + 2) = 40² – 2² = 1 600 – 4 = 1 596.

b) 102² = (100 + 2)² = 100² + 2.100.2 + 2² = 10 000 + 400 + 4 = 10 404.

c) 198² = (200 – 2)² = 200² – 2.200.2 + 2² = 40 000 – 800 + 4 = 39 204.

d) 75² – 25² = (75 + 25).(75 – 25) = 100 . 50 = 5 000.

Bài 6 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (2x – 3)³;

b) (a + 3b)³;

c) (xy –1)³.

Lời giải:

a) (2x – 3)³

= (2x)³ – 3.(2x)².3 + 3.2x.3² – 3³

= 8x³ – 36x² + 54x – 8.

b) (a + 3b)³

= a³ + 3.a².3b + 3.a.(3b)² + (3b)³

= a³ + 9a²b + 27ab² + 27b³.

c) (xy –1)³

= (xy)³ – 3.(xy)².1 + 3.xy.1² – 1³

= x³y³ – 3x²y² + 3xy – 1.

Bài 7 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (a – 5)(a² + 5a + 25);

b) (x + 2y)(x² – 2xy + 4y²).

Lời giải:

a) (a – 5)(a² + 5a + 25)

= (a – 5)(a² + a.5 + 5²)

= a³ – 5³

= a³ – 125.

b) (x + 2y)(x² – 2xy + 4y²)

= (x + 2y).[x² – x.2y + (2y)²]

= x³ + (2y)³

= x³ + 8y³.

Bài 8 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức:

a) (a – 1)(a + 1)(a² + 1);

b) (xy + 1)² – (xy – 1)².

Lời giải:

a) (a – 1)(a + 1)(a² + 1)

= (a² – 1)(a² + 1)

= (a²)² – 1²

= a⁴ – 1.

b) (xy + 1)² – (xy – 1)²

= [(xy + 1) + (xy – 1)].[(xy + 1) – (xy – 1)]

= [xy + 1 + xy – 1].[xy + 1 – xy + 1]

= 2xy.2

= 4xy.

Bài 9 trang 22 Toán 8 Tập 1: a) Cho x + y = 12 và xy = 35. Tính (x − y)².

b) Cho x – y = 8 và xy = 20. Tính (x + y)².

c) Cho x + y = 5 và xy = 6. Tính x³ + y³.

d) Cho x – y = 3 và xy = 40. Tính x³ – y³.

Lời giải:

a) Ta có: (x − y)² = x² – 2xy + y²

                           = x² + 2xy + y² – 4xy

                           = (x + y)² – 4xy

Thay x + y = 12 và xy = 35 vào biểu thức trên ta có:

(x − y)² = 12² – 4.35 = 144 – 140 = 4.

b) Ta có: (x + y)² = x² + 2xy + y²

                           = x² – 2xy + y² + 4xy

                           = (x – y)² + 4xy

Thay x – y = 8 và xy = 20 vào biểu thức trên ta có:

(x + y)² = 8² + 4.20 = 64 + 80 = 144.

c) Ta có: x³ + y³ = (x + y).(x² – xy + y²)

                           = (x + y).(x² + 2xy + y² – 3xy)

                           = (x + y).[(x + y)² – 3xy]

Thay x + y = 5 và xy = 6 vào biểu thức trên ta có:

x³ + y³ = 5.(5² – 3.6) = 5.(25 – 18) = 5.7 = 35.

d) Ta có: x³ – y³ = (x – y).(x² + xy + y²)

                           = (x – y).(x² – 2xy + y² + 3xy)

                           = (x – y).[(x – y)² + 3xy]

Thay x – y = 3 và xy = 40 vào biểu thức trên ta có:

x³ – y³ = 3.(3² – 3.40) = 3.(9 – 120) = 5.(–111) = –555.

Bài 10 trang 22 Toán 8 Tập 1: Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm. Thể tích của hình hộp chữ nhật sẽ tăng bao nhiêu nếu:

a) Chiều dài và chiều rộng tăng thêm a cm?

b) Chiều dài, chiều rộng, chiều cao đều tăng thêm a cm?

Lời giải:

Thể tích hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao đều bằng 5 cm là:

5³ = 125 (cm³).

a) Chiều dài của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Chiều rộng của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).5 = (5 + a)².5

                          = (5² + 2.5.a + a²).5

                          = (25 + 10a + a²).5

                          = 25.5 + 10a.5 + a².5

                          = 125 + 50a + 5a² (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 50a + 5a² – 125 = 5a² + 50a (cm³).

b) Chiều cao của hình hộp chữ nhật sau khi tăng thêm a cm là: 5 + a (cm).

Thể tích hình hộp chữ nhật lúc sau là:

(5 + a).(5 + a).(5 + a) = (5 + a)³

                                   = 5³ + 3.5².a + 3.5.a² + a³

                                   = 125 + 75a + 15a² + a³ (cm³).

Khi đó thể tích của hình hộp chữ nhật đã tăng thêm là:

125 + 75a + 15a² + a³ – 125 = a³ + 15a² + 75a (cm³).

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Đơn thức và đa thức nhiều biến

Bài 2: Các phép toán với đa thức nhiều biến

Bài 4: Phân tích đa thức thành nhân tử

Bài 5: Phân thức đại số

Bài 6: Cộng, trừ phân thức