Với giải SGK Toán 8 Chân trời sáng tạo trang 21 chi tiết trong Bài 3: Hằng đẳng thức đáng nhớ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Nội dung bài viết
Giải Toán 8 trang 21 Tập 1 (Chân trời sáng tạo)
Thực hành 6 trang 21 Toán 8 Tập 1: Tính:
a) (x + 2y)3;
b) (3y – 1)3.
Lời giải:
a) (x + 2y)3
= x3 + 3.x2.2y + 3.x.(2y)2 + (2y)3
= x3 + 6x2y + 12xy2 + 8y3.
b) (3y – 1)3
= (3y)3 – 3.(3y)2.1 + 3.3y.12 – 13
= 27y3 – 27y2 + 9y – 1.
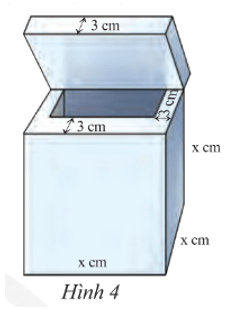
Lời giải:
Phần lòng trong của thùng chứa có dạnh hình lập phương với độ dài cạnh là x – 3 – 3 = x – 6 (cm).
Thể tích phần lòng trong của thùng là:
(x – 6)3 = x3 – 3.x2.6 + 3.x.62 – 63
= x3 – 18x2 + 108x – 216 (cm3).
Vậy dung tích (sức chứa) của thùng là x3 – 18x2 + 108x – 216 (cm3).
4. Tổng và hiệu của hai lập phương
(a + b)3 = a3 + 3a2b + 3ab2 + b3
a3 + b3 = (a + b)3 – 3a2b – 3ab2
= (a + b)3 – 3ab(a + b)
= (a + b)(…)
= …
(a – b)3 = a3 – 3a2b + 3ab2 – b3
a3 – b3 = (a – b)3 + 3a2b – 3ab2
= (a – b)3 + 3ab(a – b)
= (a – b)(…)
= …
Lời giải:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
a3 + b3 = (a + b)3 – 3a2b – 3ab2
= (a + b)3 – 3ab(a + b)
= (a + b)[(a + b)2 – 3ab]
= (a + b)(a2 + 2ab + b2 – 3ab)
= (a + b)(a2 – ab + b2).
(a – b)3 = a3 – 3a2b + 3ab2 – b3
a3 – b3 = (a – b)3 + 3a2b – 3ab2
= (a – b)3 + 3ab(a – b)
= (a – b)[(a – b)2 + 3ab]
= (a – b)(a2 – 2ab + b2 + 3ab)
= (a – b)(a2 + ab + b2).
Thực hành 7 trang 21 Toán 8 Tập 1: Viết các đa thức sau dưới dạng tích:
a) 8y3 + 1;
b) y3 – 8.
Lời giải:
a) 8y3 + 1 = (2y)3 + 1
= (2y + 1)[(2y)2 – 2y.1 + 12]
= (2y + 1)(4y2 – 2y + 1)
b) y3 – 8 = y3 – 23
= (y – 2)(y2 + y.2 + 22)
= (y – 2)(y2 + 2y + 4).
Thực hành 8 trang 21 Toán 8 Tập 1: Tính:
Lời giải:
a) (x + 1)(x2 – x + 1)
= x3 + 13
= x3 + 1.
b) .
.
Thực hành 6 trang 21 Toán 8 Tập 1: Tính:
a) (x + 2y)3;
b) (3y – 1)3.
Lời giải:
a) (x + 2y)3
= x3 + 3.x2.2y + 3.x.(2y)2 + (2y)3
= x3 + 6x2y + 12xy2 + 8y3.
b) (3y – 1)3
= (3y)3 – 3.(3y)2.1 + 3.3y.12 – 13
= 27y3 – 27y2 + 9y – 1.

Lời giải:
Phần lòng trong của thùng chứa có dạnh hình lập phương với độ dài cạnh là x – 3 – 3 = x – 6 (cm).
Thể tích phần lòng trong của thùng là:
(x – 6)3 = x3 – 3.x2.6 + 3.x.62 – 63
= x3 – 18x2 + 108x – 216 (cm3).
Vậy dung tích (sức chứa) của thùng là x3 – 18x2 + 108x – 216 (cm3).
4. Tổng và hiệu của hai lập phương
(a + b)3 = a3 + 3a2b + 3ab2 + b3
a3 + b3 = (a + b)3 – 3a2b – 3ab2
= (a + b)3 – 3ab(a + b)
= (a + b)(…)
= …
(a – b)3 = a3 – 3a2b + 3ab2 – b3
a3 – b3 = (a – b)3 + 3a2b – 3ab2
= (a – b)3 + 3ab(a – b)
= (a – b)(…)
= …
Lời giải:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
a3 + b3 = (a + b)3 – 3a2b – 3ab2
= (a + b)3 – 3ab(a + b)
= (a + b)[(a + b)2 – 3ab]
= (a + b)(a2 + 2ab + b2 – 3ab)
= (a + b)(a2 – ab + b2).
(a – b)3 = a3 – 3a2b + 3ab2 – b3
a3 – b3 = (a – b)3 + 3a2b – 3ab2
= (a – b)3 + 3ab(a – b)
= (a – b)[(a – b)2 + 3ab]
= (a – b)(a2 – 2ab + b2 + 3ab)
= (a – b)(a2 + ab + b2).
Thực hành 7 trang 21 Toán 8 Tập 1: Viết các đa thức sau dưới dạng tích:
a) 8y3 + 1;
b) y3 – 8.
Lời giải:
a) 8y3 + 1 = (2y)3 + 1
= (2y + 1)[(2y)2 – 2y.1 + 12]
= (2y + 1)(4y2 – 2y + 1)
b) y3 – 8 = y3 – 23
= (y – 2)(y2 + y.2 + 22)
= (y – 2)(y2 + 2y + 4).
Thực hành 8 trang 21 Toán 8 Tập 1: Tính:
Lời giải:
a) (x + 1)(x2 – x + 1)
= x3 + 13
= x3 + 1.
b) .
.
Xem thêm các bài giải Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Khởi động trang 18 Toán 8 Tập 1: Hãy tính nhanh 652 – 352 = ?; 102 . 98 = ?
Thực hành 1 trang 19 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức a) (3x + 1)2; b) (4x + 5y)2;
Thực hành 3 trang 19 Toán 8 Tập 1: Tính nhanh 52^2; 982.
Thực hành 5 trang 20 Toán 8 Tập 1: Tính nhanh 82 . 78; 87 . 93; 1252 – 252.
Vận dụng 2 trang 20 Toán 8 Tập 1: Giải đáp câu hỏi ở Hoạt động khởi động (trang 18)
Thực hành 6 trang 21 Toán 8 Tập 1: Tính a) (x + 2y)3;
Thực hành 7 trang 21 Toán 8 Tập 1: Viết các đa thức sau dưới dạng tích
Thực hành 8 trang 21 Toán 8 Tập 1: Tính (x + 1)(x2 – x + 1);
Bài 1 trang 22 Toán 8 Tập 1: Tính (3x + 4)2;
Bài 2 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu
Bài 3 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức
Bài 5 trang 22 Toán 8 Tập 1: Tính nhanh 38 . 42; 1022;
Bài 6 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức (2x – 3)3; (a + 3b)3; (xy –1)3.
Bài 7 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức (a – 5)(a2 + 5a + 25); (x + 2y)(x2 – 2xy + 4y2).
Bài 8 trang 22 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức: (a – 1)(a + 1)(a2 + 1); (xy + 1)2 – (xy – 1)2.
Bài 9 trang 22 Toán 8 Tập 1: a) Cho x + y = 12 và xy = 35. Tính (x − y)2.
Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Đơn thức và đa thức nhiều biến
Bài 2: Các phép toán với đa thức nhiều biến
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.