Với giải Bài 10 trang 89 Toán 8 Tập 1 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 3 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Bài 10 trang 89 Toán 8 Tập 1 | Chân trời sáng tạo Giải Toán lớp 8

Bài 10 trang 89 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh rằng tứ giác ANEB là hình thang vuông.

b) Chứng minh rằng tứ giác ANEM là hình chữ nhật.

c) Qua M kẻ đường thẳng song song với BN cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.

Lời giải:

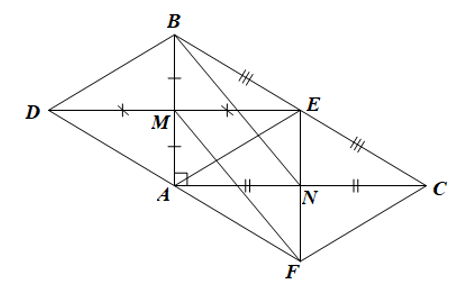
a) • Xét ABC vuông tại A có AE là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC

Suy ra $AE=EB=EC=\frac{1}{2}BC$.

• Vì EA = EC nên E nằm trên đường trung trực của AC.

Vì N là trung điểm của AC nên N nằm trên đường trung trực của AC.

Suy ra EN là đường trung trực của đoạn thẳng AC nên EN ⊥ AC.

Ta có: BA ⊥ AC và EN ⊥ AC nên BA // EN.

• Tứ giác ANEB có BA // EN nên là hình thang

Lại có $\widehat{BAN}=90°$ nên hình thang ANEB là hình thang vuông.

b) Vì EA = EB nên E nằm trên đường trung trực của AB.

Vì M là trung điểm của AB nên M nằm trên đường trung trực của AB.

Suy ra EM là đường trung trực của AB nên EM ⊥ AB, hay $\widehat{AME}=90°$.

Xét tứ giác ANEM có $\widehat{MAN}=90°$, $\widehat{ANE}=90°$, $\widehat{AME}=90°$ 

Suy ra ANEM là hình chữ nhật.

c) • Xét tứ giác BMFN có FM // BN và MB // NF (do AB // EN)

Suy ra BMFN là hình bình hành.

Do đó MB = NF.

Lại có AM = MB (do M là trung điểm AB) và AM = EN (do ANEM là hình chữ nhật)

Do đó EN = NF hay N là trung điểm của EF.

• Xét tứ giác AFCE có hai đường chéo AC và EF cắt nhau tại trung điểm của mỗi đường.

Suy ra AFCE là hình bình hành.

Lại có EF ⊥ AC nên AFCE là hình thoi.

d) • Do AFCE là hình thoi (câu c) nên AF // CE và AF = CE.

Chứng minh tương tự câu c, ta cũng có ADBE là hình thoi

Suy ra AD // BE và AD = BE.

• Ta có AF // BC (do AF // CE) và AD // BC (do AD // BE), theo tiên đề Euclid ta có AD và AF trùng nhau hay ba điểm F, A, D thẳng hàng   (1)

• Ta có AF = CE và AD = BE

Mà CE = BE (do E là trung điểm của BC)

Suy ra AF = AD (2)

• Từ (1) và (2) ta có A là trung điểm của DF.