Với giải SGK Toán 11 Cánh Diều trang 65 chi tiết trong Bài 1: Giới hạn của dãy số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 65 Tập 1 (Cánh Diều)

Bài 2 trang 65 Toán 11 Tập 1: Tính các giới hạn sau:

a) lim$\frac{5n+1}{2n}$;

b) lim$\frac{6n^2+8n+1}{5n^2+3}$;

c) lim$\frac{\sqrt{n^2+5n+3}}{6n+2}$;

d) lim$\left(2-\frac{1}{3^n}\right)$;

e) lim$\frac{3^n+2^n}{{4.3}^n}$;

g) lim$\frac{2+\frac{1}{n}}{3^n}$.

Lời giải:

a) lim$\frac{5n+1}{2n}$ = lim$\left(\frac{5}{2}+\frac{1}{2n}\right)=\lim \frac{5}{2}+\lim \frac{1}{2n}=\frac{5}{2}$.

Bài 3 trang 65 Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (u_n­), với u₁=$\frac{2}{3}$, q=-$\frac{1}{4}$.

b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số.

Lời giải:

a) Tổng của cấp số nhân lùi vô hạn (u_n), với u₁=$\frac{2}{3}$, q=-$\frac{1}{4}$là:

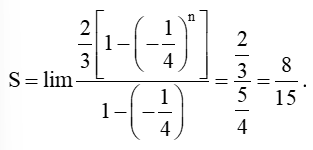
b) Ta có:

1,(6) = 1 + 0,(6) = 1 + 0,6 + 0,06 + 0,006 + ... + 0,000006 + ...

Dãy số 0,6; 0,006; 0,0006; ... lập thành một cấp số nhân có số hạng đầu u₁ = 0,6 và công bội q = $\frac{1}{10}$có |q| < 1 nên ta có:

0,6 + 0,06 + 0,006 + ... + 0,000006 + ... =$\frac{0,6}{1-\frac{1}{10}}=\frac{2}{3}$.

Suy ra 1,(6) = 1 + $\frac{2}{3}$=$\frac{5}{3}$.

Bài 4 trang 65 Toán 11 Tập 1: Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn.

a) Tính diện tích S_n của hình vuông được tạo thành ở bước thứ n;

b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.

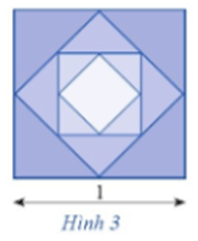
Lời giải:

a) Gọi S_n là diện tích của hình vuông thứ n.

Ta có: S₁ = 1; S₂ = $\frac{1}{2}$; S₃ = ${\left(\frac{1}{2}\right)}^2$; ...

Dãy (S_n) lập thành cấp số nhân có số hạng đầu S₁ = 1 và công bội q = $\frac{1}{2}$có công thức tổng quát là: Sn = ${\left(\frac{1}{2}\right)}^{n-1}$.

b) Ta có: |q|=|$\frac{1}{2}$|<1nên dãy (S_n­) trên lập thành một cấp số nhân lùi hạn nên ta có:

S = 1+$\frac{1}{2}+{\left(\frac{1}{2}\right)}^2+{\left(\frac{1}{2}\right)}^3+\mathrm{...}+{\left(\frac{1}{2}\right)}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{1}{2}}=2$.

Vậy tổng diện tích của các hình vuông là 2 (đvdt).

Bài 5 trang 65 Toán 11 Tập 1: Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm thì một nửa số chất phóng xạ này bị phân ra thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã).

(Nguồn: Đại số và Giải tích 11, NXB GD Việt Nam, 2021).

Gọi u_n là khối lượng chất phóng xạ còn lại sau chu kì thứ n.

a) Tìm số hạng tổng quát u_n của dãy số (u_n).

b) Chứng minh rằng (u_n) có giới hạn là 0.

c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn bé lại bé hơn 10^{– 6} g.

Lời giải:

a) Ta có: u₁ = 1; u₂ = $\frac{1}{2}$; u₃ = ${\left(\frac{1}{2}\right)}^2$; ...

Suy ra (u_n­) lập thành một cấp số nhân có số hạng đầu u₁ = 1 và q = $\frac{1}{2}$có số hạng tổng quát là: $u_n={\left(\frac{1}{2}\right)}^{n-1}$.

b) Ta có: lim$u_n=\lim {\left(\frac{1}{2}\right)}^{n-1}$=0.

c) Đổi $u_n={\left(\frac{1}{2}\right)}^{n-1}kg={\left(\frac{1}{2}\right)}^{n-1}{.10}^{3}g$

Để chất phóng xạ bé hơn 10^-6 (g) thì ${\left(\frac{1}{2}\right)}^{n-1}{.10}^3<{10}^{-6}\iff$n>31.

Vậy cần ít nhất 30 chu kì tương ứng với 720 000 năm khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người.

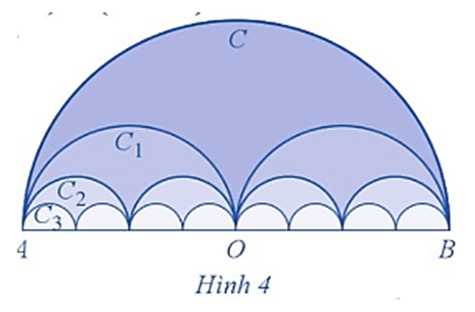
Bài 6 trang 65 Toán 11 Tập 1: Gọi C là nửa đường tròn đường kính AB = 2R.

C₁ là đường gồm hai nửa đường tròn đường kính $\frac{AB}{2}$.

C₂ là đường gồm bốn nửa đường tròn đường kính $\frac{AB}{4}$, ...

C_n là đường gồm 2ⁿ nửa đường tròn đường kính $\frac{AB}{2^n}$,...(Hình 4).

Gọi P_n là độ dài của C_n­, S_n là diện tích hình phẳng giới hạn bởi C_n và đoạn thẳng AB.

a) Tính p_n, S_n.

b) Tìm giới hạn của các dãy số (p_n) và (S_n).

Lời giải:

a)

+) Ta có: p₁ = $\frac{\pi R}{2}$; p₂ = $\frac{\pi R}{4}=\frac{\pi R}{2^2}$; p₃ = $\frac{\pi R}{8}=\frac{\pi R}{2^3}$; ...

(p_n) lập thành một cấp số nhân lùi vô hạn với số hạng đầu p₁ = $\frac{\pi R}{2}$và công bội q = $\frac{1}{2}$<1 có số hạng tổng quát p_n = $\frac{\pi R}{2}.{\left(\frac{1}{2}\right)}^{n-1}$.

+) Ta có: C₁ = $\frac{\pi R^2}{4}$; C₂ = $\frac{\pi R^2}{4^2}$; C₃ = $\frac{\pi R^3}{4^3}$; ...

(C_n) lập thành một cấp số nhân lùi vô hạn với số hạng đầu C₁ = $\frac{\pi R^2}{4}$và công bội q = $\frac{1}{4}$<1có số hạng tổng quát C_n = $\frac{\pi R}{4}.{\left(\frac{1}{4}\right)}^{n-1}$.