Toptailieu.vn biên soạn và giới thiệu Ứng dụng tích phân tính diện tích hình phẳng: Phương pháp giải và bài tập hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Ứng dụng tích phân tính diện tích hình phẳng, từ đó học tốt môn Toán.

Ứng dụng tích phân tính diện tích hình phẳng: Phương pháp giải và bài tập hay, chi tiết

A. LÝ THUYẾT.

1. Diện tích hình phẳng giới hạn bởi một đường cong và trục hoành.

Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số  y = f(x) liên tục, trục hoành và hai đường thẳng x = a; x = b được tính theo công thức

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$ (1)

Chú ý: Để tính diện tích S ta phải tính tích phân (1), muốn vậy ta phải phá dấu giá trị tuyệt đối:

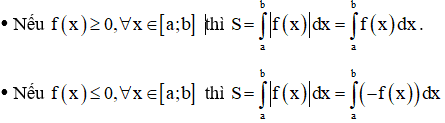
Muốn xét dấu của biểu thức f(x) ta thường có một số cách làm như sau:

Cách 1: Sử dụng bảng xét dấu cho f(x) với ghi nhớ qua nghiệm bội lẻ f(x) đổi dấu, qua nghiệm bội chẵn f(x) không đổi dấu.

Cách 2: Dựa vào đồ thị của hàm số y = f(x) trên đoạn [a; b] để suy ra dấu của f(x) trên đoạn đó:

- Nếu trên đoạn [a; b] đồ thị hàm số y = f(x) nằm phía trên trục hoành thì $f\left(x\right)\ge 0,\forall x\in \left[a;b\right]$.

- Nếu trên đoạn [a; b] đồ thị hàm số y = f(x) nằm phía dưới trục hoành thì $f\left(x\right)\le 0,\forall x\in \left[a;b\right]$.

Cách 3: Nếu f(x) không đổi dấu trên [a; b] thì ta có: $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|d\text{x}=\left|\underset{a}{\overset{b}{\int }}f\left(x\right)dx\right|$

Cách 4: Sử dụng máy tính CASIO, tuy nhiên xu hướng ra đề thi THPT Quốc gia sẽ hạn chế CASIO nên cần chú ý cách giải tổng quát và hiểu rõ bản chất!

2. Diện tích hình phẳng giới hạn bởi hai đường cong.

Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b].

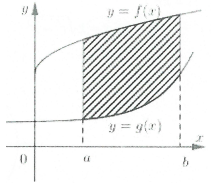
Khi đó diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) và hai đường thẳng x = a, x = b là $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$.

Tương tự như chú ý ở trên thì ở bài toán này ta cũng phải xét đoạn mà dấu của $f\left(x\right)-g\left(x\right)$ không đổi.

Chú ý:

- Giả sử phương trình có hai nghiệm $c;d\left(c<d\right)$. Khi đó $f\left(x\right)-g\left(x\right)$ không đổi dấu trên các đoạn $\left[a;b\right],\left[c;d\right],\left[d;b\right]$. Trên mỗi đoạn đó, chẳng hạn trên đoạn $\left[a;c\right]$ thì ta có:

$\underset{a}{\overset{c}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx=\left|\underset{a}{\overset{c}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx\right|$

- Khi tính diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số ta có:

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|d\text{x}=\underset{a}{\overset{b}{\int }}\left|h\left(x\right)\right|d\text{x}$

 ta xét dấu bằng cách làm hoàn toàn tương tự như trên phần 1.

- Nếu đề bài không cho các đường thẳng giới hạn x = a; x = b ta giải phương trình f(x) = g(x) (hoặc f(x) = 0 trong trường hợp g(x) là trục hoành) để tìm cận của tích phân.

3. Ứng dụng tính diện tích hình tròn và hình Elip

a) Tính diện tích hình tròn

 Trong hệ tọa độ Oxy cho đường tròn có phương trình: $x^2+y^2=r^2\left(r>0\right)$. Khi đó hình tròn đó có diện tích là: $S=\pi r^2$

Ta có:

$x^2+y^2=r^2\iff y=\pm \sqrt{r^2-x^2}$

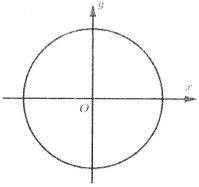
Với $y\ge 0$, ta có: $y=\sqrt{r^2-x^2}$ có đồ thị là nửa đường tròn phía trên trục hoành.

Bằng cách đặt $x=r\sin t$ ta có diện tích $S_1=\underset{-r}{\overset{r}{\int }}\sqrt{r^2-x^2}dx=2\underset{0}{\overset{r}{\int }}\sqrt{r^2-x^2}dx=\frac{\pi r^2}{2}$

Do đó $S=2{\text{S}}_1=\pi r^2$.

b) Tính diện tích hình Elip

Trong hệ tọa độ Oxy cho elip có phương trình: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,0<b<a$.

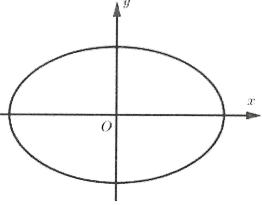
Chứng minh tương tự ta có diện tích của elip là: $S=\pi ab$ (đvdt).

B. VÍ DỤ MINH HOẠ.

Ví dụ 1. Tính diện tích hình phẳng (hình được tô màu) được biểu diễn ở hình dưới.

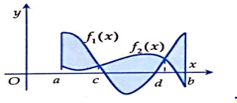
Lời giải

Nhận thấy trên $\left[a;c\right]$ và $\left[d;b\right]$ thì $f_1\left(x\right)\ge f_2\left(x\right)$; trên $\left[c;d\right]$ thì  $f_1\left(x\right)\le f_2\left(x\right)$

Do vậy:

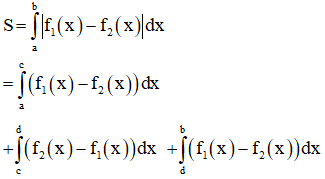
(Trên đây là cách bỏ dấu giá trị tuyệt đối)

Ví dụ 2. Tính diện tích hình phẳng trên được giới hạn bởi đồ thị hàm số $y=-x^2+2\text{x}-2$, trục hoành và các đường thẳng x = 0; x = 3.

Lời giải

Diện tích S của hình phẳng trên là $S=\underset{0}{\overset{3}{\int }}\left|-x^2+2\text{x}-2\right|d\text{x}$.

Ta có: 

$-x^2+2\text{x}-2\le 0,\forall x\in \left[0;3\right]$

$$\begin{gathered} S=\underset{0}{\overset{3}{\int }}\left|-x^2+2\text{x}-2\right|d\text{x} \\ =\underset{0}{\overset{3}{\int }}\left(x^2-2\text{x}+2\right)d\text{x} \\ = {\left.\left(\frac{x^3}{3}-x^2+2\text{x}\right)\right|}_0^3=6 \left(đvdt\right). \end{gathered}$$

Ví dụ 3. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y=x^2-x+1,y=x+1$ là

A. $-\frac{4}{3}$

B. $\frac{4}{3}$

C. 1

D.  $\frac{2}{3}$

Lời giải

Phương trình hoành độ giao điểm 2 đồ thị là:

$$\begin{gathered} x^2-x+1=x+1 \\ \iff x^2-2\text{x}=0\iff \left[\begin{array}{l}x=0\\ x=2\end{array}\right. \end{gathered}$$

Diện tích cần tìm là:

$$\begin{gathered} S=\underset{0}{\overset{2}{\int }}\left|x^2-x+1-x-1\right|d\text{x} \\ =\underset{0}{\overset{2}{\int }}\left|x^2-2\text{x}\right|d\text{x}=\underset{0}{\overset{2}{\int }}\left(2\text{x}-x^2\right)d\text{x} \\ ={\left.\left(x^2-\frac{x^3}{3}\right)\right|}_0^2=\frac{4}{3} \end{gathered}$$

Chọn B.

Ví dụ 4. Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số $y=e^x+x$ và các đường thẳng $x-y+1=0,x=\ln 5$.

A. $S=5-\ln 4$

B. $S=4-\ln 5$

C. $S=4+\ln 5$

D.  $S=5+\ln 4$

Lời giải

Ta có: 

$$\begin{gathered} x-y+1=0 \\ \iff y=x+1 \end{gathered}$$

Phương trình hoành độ giao điểm của hai đồ thị là:

$$\begin{gathered} e^x+x=x+1 \\ \iff e^x=1\iff x=0 \end{gathered}$$

Diện tích hình phẳng cần tìm là:

$$\begin{gathered} S=\underset{0}{\overset{\ln 5}{\int }}\left|e^x-1\right|d\text{x} \\ =\underset{0}{\overset{\ln 5}{\int }}\left(e^x-1\right)d\text{x}={\left.\left(e^x-x\right)\right|}_0^{\ln 5}=4-\ln 5 \end{gathered}$$

Chọn B.

Ví dụ 5. Tính diện tích của các hình phẳng giới hạn bởi: Parabol $y=x^2-2x+2$, tiếp tuyến của nó tại điểm M(3; 5) và trục tung.

A. 10

B. 8

C. 9

D. 12

Lời giải

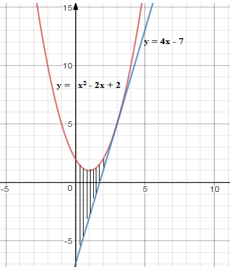
Chọn C.

C. BÀI TẬP TỰ LUYỆN.

Câu 1. Viết công thức tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b) là:

A. $S=\underset{a}{\overset{b}{\int }}f\left(x\right)\text{d}x.$

B. $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|\text{d}x.$

C. $S=\underset{a}{\overset{b}{\int }}{f}^2\left(x\right)\text{d}x.$

D. $S=\pi \underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|\text{d}x.$

Câu 2. Cho đồ thị hàm số y = f(x). Diện tích S của hình phẳng (phần tô đậm trong hình dưới) là:

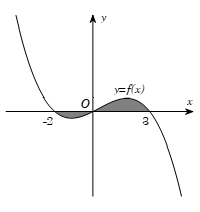
A. $S=\underset{-2}{\overset{3}{\int }}f\left(x\right)\text{d}x$

B. $S=\underset{-2}{\overset{0}{\int }}f\left(x\right)\text{d}x+\underset{0}{\overset{3}{\int }}f\left(x\right)\text{d}x$

C. $S=\underset{0}{\overset{-2}{\int }}f\left(x\right)\text{d}x+\underset{0}{\overset{3}{\int }}f\left(x\right)\text{d}x$

D. $S=\underset{-2}{\overset{0}{\int }}f\left(x\right)\text{d}x+\underset{3}{\overset{0}{\int }}f\left(x\right)\text{d}x$

Câu 3. Diện tích của hình phẳng giới hạn bởi đồ thị hai hàm số $y=x^2+2$ và $y=3x$ là:

A. $S=2$

B. $S=3$

C. $S=\frac{1}{2}$

D. $S=\frac{1}{6}$.

Câu 4. Kết quả của diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=-x^3+3x^2-2$, trục hoành, trục tung và đường thẳng x = 2 có dạng $\frac{a}{b}$ (với $\frac{a}{b}$ là phân số tối giản). Khi đó mối liên hệ giữa a và b là:

A. $a-b=2.$

B. $a-b=3$

C. $a-b=-2.$

D. $a-b=-3$

Câu 5. Kết quả của việc tính diện tích hình phẳng giới hạn bởi đồ thị $\left(C\right):y=x^4-2x^2+1$ và trục Ox gần nhất với giá trị nào sau đây?

A. $S=\frac{1}{2}.$

B. $S=1.$

C. $S=\frac{3}{2}.$

D. $S=2.$

Câu 6. Diện tích hình phẳng giới hạn bởi các đường $y=x\sqrt{1+x^2}$, trục hoành và đường thẳng x = 1 là:

A. $S=\frac{1}{3}.$

B. $S=\frac{2\sqrt{2}-1}{3}.$

C. $S=\frac{2\sqrt{2}+1}{3}.$

D. $S=2\left(\sqrt{2}-1\right).$

Câu 7. Diện tích hình phẳng giới hạn bởi các đường $y=\sqrt{x}$ và $x-2y=0$ bằng với diện tích hình nào sau đây:

A. Diện tích hình vuông có cạnh bằng 2.

B. Diện tích hình chữ nhật có chiều dài, chiều rộng lần lượt 5 và 3.

C. Diện tích hình tròn có bán kính bằng 3.

D. Diện tích toàn phần khối tứ diện đều có cạnh bằng $\frac{2\sqrt[4]{3}}{3}$.

Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\frac{2}{{\left(x+1\right)}^2}$, trục hoành, đường thẳng x = 0 và đường thẳng x = 4 là:

A. $S=-\frac{8}{5}.$

B. $S=\frac{8}{5}.$

C. $S=\frac{2}{25}.$

D. $S=\frac{4}{25}.$

Câu 9. Tính diện tích hình phẳng giới hạn bởi các đường y = xlnx, trục hoành và đường thẳng x = e.

A. $S=\frac{e^2+1}{4}$

B. $S=\frac{e^2+1}{6}$

C. $S=\frac{e^2+1}{8}$

D. $S=\frac{e^2+1}{2}$

Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=e^x+x$, trục hoành, trục tung và đường thẳng  x = 1 là:

A. $S=e+\frac{1}{2}.$

B. $S=e-\frac{1}{2}.$

C. $S=e+1.$

D. $S=e-1.$

Câu 11. Gọi S là diện tích hình phẳng giới hạn bởi các đường $y=\left(e+1\right)x$ và $y=\left(1+e^x\right)x$. Giá trị  cần tìm là:

A. $S=\frac{e+2}{2}$

B. $S=\frac{e}{2}$

C. $S=\frac{e-2}{2}$

D. $S=\frac{e-2}{4}$

Câu 12. Tính diện tích hình phẳng giới hạn bởi nửa đường tròn $y=\sqrt{2-x^2}$ và đường thẳng d đi qua hai điểm $A(-\sqrt{2};0)$ và B(1; 1)  (phần tô đậm như hình vẽ).

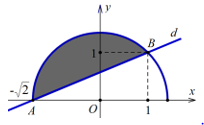
A. $\frac{\pi +2\sqrt{2}}{4}.$

B. $\frac{3\pi +2\sqrt{2}}{4}.$

C. $\frac{\pi -2\sqrt{2}}{4}.$

D. $\frac{3\pi -2\sqrt{2}}{4}.$

Câu 13. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=4-\frac{1}{x^2}$ đường thẳng y = - 1, đường thẳng y = 1 và trục tung được tính như sau:

A. $S=\underset{-1}{\overset{1}{\int }}\left(4-\frac{1}{x^2}\right)\text{d}x$

B. $S=\underset{-1}{\overset{1}{\int }}\left|4-\frac{1}{x^2}\right|\text{d}x.$

C. $S=\underset{-1}{\overset{1}{\int }}\frac{1}{\sqrt{4-y}}.$

D. $S=\underset{-1}{\overset{1}{\int }}\frac{-1}{\sqrt{4-y}}\text{d}y.$

Câu 14. Diện tích của hình phẳng giới hạn bởi hai đường cong có phương trình $x-y^2=0$ và $x+2y^2-12=0$ bằng:

A. S = 15

B. S = 32.

C. S = 25

D. S = 30

Câu 15. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sin x + 1, trục hoành và hai đường thẳng x = 0 và $x=\frac{7\pi }{6}$.

A. $\frac{\sqrt{3}}{2}+\frac{7\pi }{6}-1$

B. $\frac{\sqrt{3}}{2}+\frac{7\pi }{6}+1$

C. $\frac{\sqrt{3}}{2}+\frac{7\pi }{3}+1$

D. $\frac{\sqrt{3}}{4}+\frac{7\pi }{6}-1$

Câu 16. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{x}$ và $y=\sqrt[3]{x}$.

A. $\frac{1}{12}$

B. $\frac{1}{9}$

C. $\frac{1}{8}$

D. $\frac{1}{15}$

Câu 17. Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y=2x^2$ và $y=x^4-2x^2$ trong miền x > 0.

A. $\frac{34}{15}$

B. $\frac{14}{15}$

C. $\frac{64}{15}$

D. $\frac{32}{15}$

Câu 18. Tính diện tích hình phẳng giới hạn bởi parabol: $y=x^2+1$, tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy.

A. $\frac{5}{6}$

B. $\frac{9}{11}$

C. $\frac{8}{3}$

D. $\frac{5}{2}$

Câu 19. Tính diện tích của những hình phẳng được giới hạn bởi các đường cong $y=x^3;y=x;y=2x.$

A. $\frac{7}{3}$

B. $\frac{5}{4}$

C. $\frac{3}{2}$

D. $\frac{1}{2}$

Câu 20. Tính diện tích của những hình phẳng được giới hạn bởi các đường cong $y^2=2x+1;y=x-1$

A. $\frac{7}{3}$

B. $\frac{16}{3}$

C. $\frac{21}{11}$

D. $\frac{8}{9}$

Câu 21. Tính diện tích giới hạn bởi $\left\{\begin{array}{c}\begin{array}{c}y=e^x\\ y=e^{-x}\end{array}\\ x=1\end{array}\right.$.

A. $2e+\frac{3}{e}-2$

B. $e+\frac{2}{e}-1$

C. $e+\frac{1}{e}-2$

D. $2e+\frac{1}{e}$

Câu 22. Tính diện tích giới hạn bởi: $y=\frac{1}{2}\left(x^2-4x+3\right)$ và hai tiếp tuyến xuất phát từ $M\left(3;-2\right)$.

A. 8

B. 5

C. 13

D. 11

Câu 23. Gọi (D) là miền giới hạn bởi: $y=-3x+10$; $y=1,y=x^2\left(x>0\right)$ và (D) ở ngoài $\left(P\right):y=x^2$.

A. $\frac{11}{12}$

B. $\frac{7}{2}$

C. $\frac{34}{13}$

D. $\frac{17}{6}$

Câu 24. Tính diện tích giới hạn bởi: $\left\{\begin{array}{c}y=x\sqrt{1-x^2},y=0\\ x=0,x=1\end{array}\right.$

A. $\frac{1}{3}$

B. $\frac{5}{4}$

C. $\frac{1}{4}$

D. $\frac{1}{2}$

Câu 25. Tính diện tích phần mặt phẳng bị giới hạn bởi đồ thị hàm số $y=\left(x+1\right)\sin x$ với đường thẳng $x=-\pi ;x=0$ và trục Ox.

A. $\pi -2\sin 1$

B. $\pi -2$

C. $\pi$

D. $\pi -\sin 1$

Câu 26. Tính diện tích phần mặt phẳng bị giới hạn bởi đồ thị hàm số $y=e^x\cos 2x$ với đường thẳng $x=0;x=\frac{\pi }{4}$ và trục Ox.

A. $\frac{e^{\frac{\pi }{4}}-1}{3}$

B. $\frac{e^{\frac{\pi }{4}}-1}{7}$

C. $\frac{e^{\frac{\pi }{4}}-1}{2}$

D. $\frac{e^{\frac{\pi }{4}}-1}{5}$

Câu 27. Cho (H) là hình phẳng giới hạn bởi parabol $y=\sqrt{3}{x}^2$ và nửa đường tròn có phương trình $\text{y=}\sqrt{{\text{4-x}}^{\text{2}}}$ với -2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng?

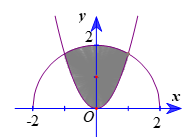
A. $\frac{2\pi +5\sqrt{3}}{3}.$

B. $\frac{4\pi +5\sqrt{3}}{3}.$

C. $\frac{4\pi +\sqrt{3}}{3}.$

D. $\frac{2\pi +\sqrt{3}}{3}.$

Câu 28. Kí hiệu  S₁, S₂, S₃ lần lượt là diện tích hình vuông có cạnh là 1, hình tròn có bán kính bằng 1, hình phẳng giới hạn bởi hai đường $\text{y=2}\sqrt{{\text{1-x}}^{\text{2}}}\text{;y=2(1-x).}$ Tính tỉ số $\frac{S_1+S_3}{S_2}.$

A. $\frac{1}{5}.$

B. $\frac{1}{3}.$

C. $\frac{1}{2}.$

D. $\frac{1}{4}.$

Đáp án

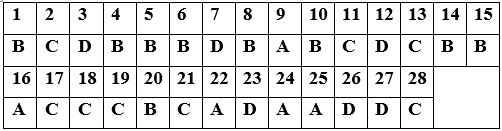
Xem thêm các dạng Toán lớp 12 hay, chi tiết khác:

Các phương pháp tính tích phân và cách giải

Tích phân hàm phân thức hữu tỉ và lượng giác và cách giải

Ứng dụng của tích phân tính thể tích khối tròn xoay và cách giải

Các bài toán thực tế ứng dụng tích phân và cách giải

Các công thức nguyên hàm cơ bản đầy đủ, chi tiết nhất