Toptailieu.vn biên soạn và giới thiệu Các công thức nguyên hàm cơ bản hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Các công thức nguyên hàm cơ bản, từ đó học tốt môn Toán.
Các công thức nguyên hàm cơ bản đầy đủ, chi tiết
1. Lý thuyết
a) Định nghĩa:
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x∈K.
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu .
b) Tính chất của nguyên hàm
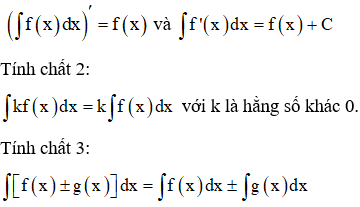
c) Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
d. Bảng nguyên hàm của một số hàm số sơ cấp
Nhận xét. Khi thay x bằng (ax + b) thì lấy nguyên hàm nhân kết quả thêm
2. Ví dụ minh họa
Ví dụ 1: Tính nguyên hàm của các hàm số sau:
a) f(x)= x3 + 3x + 2
b)
c) f(x) = (x + 1)(x + 2)
d)
Lời giải
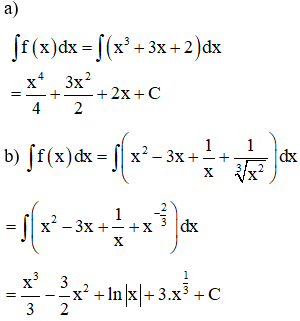
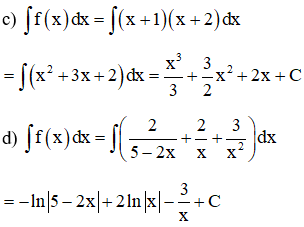
Ví dụ 2: Tính các nguyên hàm
a)
b)
c)
Lời giải
a)
b)
c)
Xem thêm các dạng bài tập Toán hay, chi tiết khác:
Ứng dụng của tích phân tính thể tích khối tròn xoay và cách giải
Các bài toán thực tế ứng dụng tích phân và cách giải
Các công thức nguyên hàm mở rộng đầy đủ, chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
