Toptailieu.vn biên soạn và giới thiệu Nhận biết khối đa diện lồi, đều hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Nhận biết khối đa diện lồi, đều, từ đó học tốt môn Toán.

Nhận biết khối đa diện lồi, đều: Phương pháp giải và bài tập hay, chi tiết

I. LÝ THUYẾT

1. Khối đa diện lồi

Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn luôn thuộc (H).

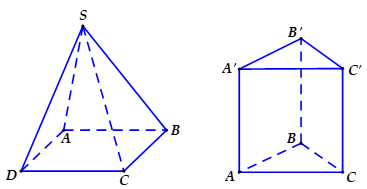
2. Khối đa diện đều

Khối đa diện đều là khối đa diện lồi có tính chất sau đây:

+) Mỗi mặt của nó là một đa giác đều n cạnh.

+) Mỗi đỉnh của nó là đỉnh chung của đúng p mặt.

Khối đa diện đều như vậy được gọi là khối đa diện đều loại {n; p}.

Chỉ có năm loại khối đa diện đều. Đó là loại {3; 3}, {4; 3}, {3; 4}, {5; 3}, {3; 5}.

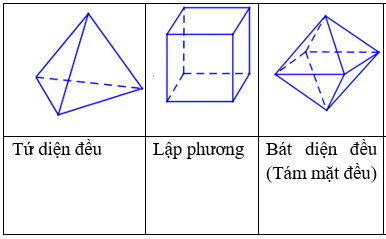
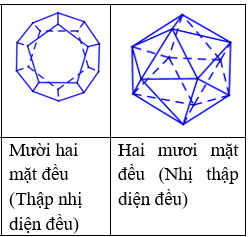
Bảng tóm tắt của năm loại khối đa diện đều

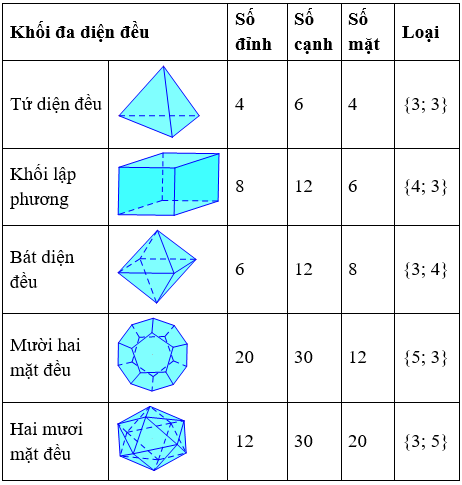
Lưu ý: Tính đối xứng của các khối đa diện đều.

+) Tứ diện đều:

3 trục đối xứng (đoạn nối trung điểm của hai cạnh đối diện):

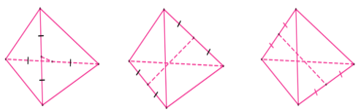
Có 6 mặt đối xứng. Mỗi mặt phẳng đều chứa 1 cạnh và trung điểm cạnh đối diện:

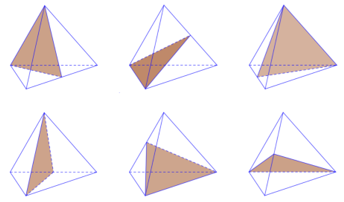
+) Khối lập phương: Có 9 mặt đối xứng. Trong đó:

3 mặt phẳng đi qua trung điểm 4 cạnh song song với nhau chia khối lập phương thành 2 khối hộp chữ nhật.

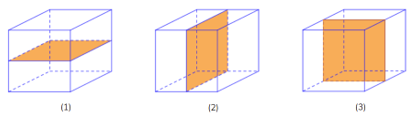
6 mặt còn lại chia khối lập phương thành 2 khối lăng trụ tam giác bằng nhau.

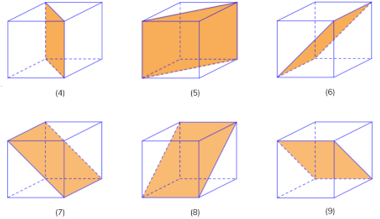
+) Bát diện đều: Bát diện đều có tất cả 9 mặt đối xứng. Trong đó:

3 mặt chia bát diện đều thành 2 khối chóp tứ giác đều mà có tất cả các cạnh bằng nhau.

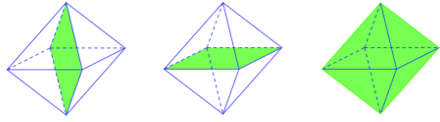
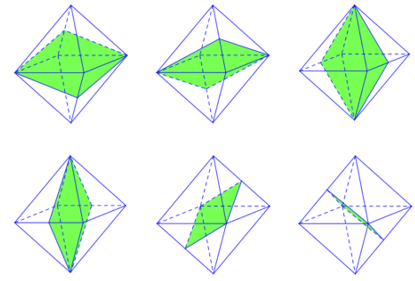
6 mặt đối xứng còn lại của bát diện đều đi qua 1 cặp đỉnh đối diện. Mỗi cặp đỉnh có 2 mặt phẳng đối xứng.

+) Mười hai mặt đều: 15 mặt phẳng đối xứng.

+) Hai mươi mặt đều: 15 mặt phẳng đối xứng.

3. Một số kết quả quan trọng

a) Kết quả 1: Cho một khối tứ diện đều. Khi đó:

+ Các trọng tâm của các mặt của nó là các đỉnh của một tứ diện đều.

+ Các trung điểm của các cạnh của nó là các đỉnh của một khối bát điện đều (khối tám mặt đều).

b) Kết quả 2: Tâm của các mặt của một khối lập phương là các đỉnh của một bát diện đều.

c) Kết quả 3: Tâm của các mặt của một bát diện đều là các đỉnh của một hình lập phương.

d) Kết quả 4: Hai đỉnh của một bát diện đều được gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối bát diện đều. Khi đó:

+ Ba đường chéo cắt nhau tại trung điểm của mỗi đường;

+ Ba đường chéo đôi một vuông góc với nhau;

+ Ba đường chéo bằng nhau.

II. PHƯƠNG PHÁP

Tính toán một số thông tin liên quan đến các khối đa diện lồi, đều.

Phương pháp : Gọi Đ là tổng số đỉnh, C là tổng số cạnh và M là tổng các mặt của khối đa diện đều loại {n ; p}. Ta có:

III. VÍ DỤ MINH HỌA

Ví dụ 1: Khối mười hai mặt đều {mỗi mặt là ngũ giác đều} có mấy cạnh?

A. 16.

B. 18.

C. 20.

D. 30.

Hướng dẫn giải

Khối 12 mặt đều có số mặt là M = 12.

Mỗi mặt là ngũ giác đều nên số cạnh một mặt là n = 5.

Áp dụng công thức 2C = nM ta được:

2C = 5.12 suy ra .

Vậy tổng số cạnh của khối mười hai mặt đều là 30.

Chọn D.

Ví dụ 2: Cho đa diện (H) có tất cả các mặt đều là tam giác. Khẳng định nào sau đây đúng?

A. Tổng các mặt của (H) luôn là một số chẵn.

B. Tổng các mặt của (H) luôn gấp đôi tổng số đỉnh của (H).

C. Tổng số các cạnh của (H) là một số không chia hết cho 3.

D. Tổng số các cạnh của (H) luôn gấp đôi tổng số các mặt của (H)

Hướng dẫn giải

Gọi tổng số mặt của (H) là M và tổng số các cạnh của (H) là C.

Vì các mặt của đa diện đều là tam giác, nên số cạnh của một mặt là n = 3.

Áp dụng công thức 2C = nM suy ra 2C = 3M

Suy ra M là một số chẵn.

Chọn A.

Ví dụ 3: Cho hình đa diện đều loại {4; 3} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?

A. $S=4a^2.$

B. $S=6a^2.$

C. $S=8a^2.$

D. $S=10a^2.$

Hướng dẫn giải

Đa diện đều loại {4; 3} là khối lập phương nên có 6 mặt là các hình vuông cạnh a.

Diện tích một mặt hình lập phương là: $S_1=a^2$

Vậy hình lập phương có tổng diện tích tất cả các mặt là $S=6S_1=6a^2.$

Chọn B.

IV. BÀI TẬP ÁP DỤNG

Câu 1: Tìm mệnh đề sai trong các mệnh đề sau

A. Khối tứ diện đều có 6 cạnh.

B. Khối lập phương có 12 cạnh.

C. Số cạnh của một khối chóp là chẵn.

D. Khối 8 mặt đều có 8 cạnh.

Câu 2. Trong một khối đa diện lồi với các mặt là các tam giác, nếu gọi C là số cạnh và M là số mặt thì hệ thức nào sau đây đúng?

A. 2M = 3C.

B. 3M = 2C.

C. 3M = 5C.

D. 2M = C.

Câu 3. Trong một khối đa diện lồi mà mỗi đỉnh là đỉnh chung của ba cạnh, nếu gọi C là số cạnh và Đ là số mặt thì hệ thức nào sau đây đúng?

A. 3Đ = 2C.

B. 3Đ = C.

C. 4Đ = 3C.

D. C = 2Đ.

Câu 4. Khối mười hai mặt đều (mỗi mặt là ngũ giác đều) có mấy đỉnh?

A. 16.

B. 18.

C. 20.

D. 30.

Câu 5. Khối hai mươi mặt đều (mỗi mặt là tam giác đều) có mấy cạnh?

A. 16. 

B. 18. 

C. 20.

D. 30.

Câu 6. Trong các loại khối đa diện đều sau, khối đa diện có số cạnh gấp đôi số đỉnh là

A. Khối hai mươi mặt đều.

B. Khối lập phương.

C. Khối bát diện đều.

D. Khối mười hai mặt đều.

Câu 7. Trong các loại khối đa diện đều sau, khối đa diện có số đỉnh và số mặt bằng nhau là

A. Khối 12 mặt đều.

B. Khối lập phương.

C. Khối bát diện đều.

D. Khối tứ diện đều.

Câu 8. Mỗi đỉnh của bát diện đều là đỉnh chung của mấy cạnh?

A. 3.

B. 4.

C. 6.

D. 5.

Câu 9. Cho khối đa diện đều. Khẳng định nào sau đây sai

A. Số đỉnh của khối lập phương bằng 8.

B. Số mặt của khối tứ diện đều bằng 4.

C. Khối bát diện đều là loại {4;3}.

D. Số cạnh của bát diện đều bằng 12.

Câu 10.  Trong các mệnh đề sau mệnh đề nào là đúng?

A. Khối đa diện đều là khối đa diện có tất cả các cạnh bằng nhau.

B. Khối đa diện đều là khối đa diện có tất cả các mặt là các đa giác đều.

C. Khối đa diện đều là khối đa diện có tất cả các mặt là các đa giác đều bằng nhau và các cạnh bằng nhau.

D. Có vô số khối đa diện đều lồi không có cùng số cạnh.

BẢNG ĐÁP ÁN

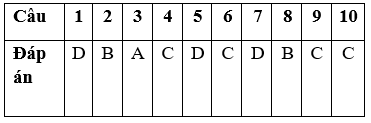
Xem thêm các dạng Toán lớp 12 hay, chi tiết khác:

Công thức tính thể tích khối tròn xoay đầy đủ, chi tiết nhất

Nhận dạng khối đa diện và cách giải

Thể tích khối đa diện và cách giải bài tập

Thể tích khối chóp và cách giải bài tập

Thể tích khối lăng trụ và cách giải bài tập