Toptailieu biên soạn và giới thiệu lời Giải Toán 8 Bài tập cuối chương 4 trang 89 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 8 Bài tập cuối chương 4 trang 89 từ đó học tốt môn Toán 8.

Toán 8 (Kết nối tri thức): Bài tập cuối chương 4 trang 89

Trắc nghiệm

Giải Toán 8 trang 89

Bài 4.18 trang 89 Toán 8 Tập 1: Độ dài x trong Hình 4.31 bằng

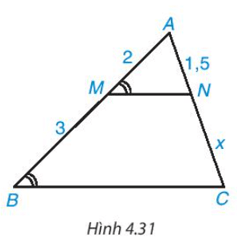
A. 2,75

B. 2.

C. 2,25.

D. 3,75.

Lời giải:

Đáp án đúng là: C

Trong Hình 4.31 có $\widehat{AMN}=\widehat{ABC}$ mà hai góc này ở vị trí đồng vị nên MN // BC.

Áp dụng định lí Thalès vào tam giác ABC, ta có:

$\frac{AM}{BM}=\frac{AN}{CN}$ hay $\frac{2}{3}=\frac{\mathrm{1,5}}{x}$.

Suy ra $x=\frac{\mathrm{1,5}.3}{2}=\mathrm{2,25}$.

Vậy x = 2,25.

Bài 4.19 trang 89 Toán 8 Tập 1: Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng

A. 3,5 cm.

B. 7 cm.

C. 10 cm.

D. 15 cm.

Lời giải:

Vì H, K lần lượt là trung điểm của AC, BC nên HK là đường trung bình của tam giác ABC suy ra $HK=\frac{1}{2}AB$.

Do đó AB = 2HK = 2 . 3,5 = 7 (cm).

Vậy AB = 7 cm.

Bài 4.20 trang 89 Toán 8 Tập 1: Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là

A. 8 cm.

B. 64 cm.

C. 30 cm.

D. 16 cm.

Lời giải:

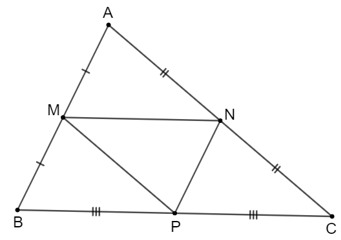
Đáp án đúng là: D

• Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra $MN=\frac{1}{2}BC$.

• Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra $NP=\frac{1}{2}AB$.

• Vì M, P lần lượt là trung điểm của các cạnh AB, BC nên NP là đường trung bình của tam giác ABC suy ra $MP=\frac{1}{2}AC$.

Chu vi tam giác ABC bằng: AB + BC + CA = 32 (cm).

Chu vi tam giác MNP bằng:

$MN+NP+MP=\frac{1}{2}BC+\frac{1}{2}AB+\frac{1}{2}AC$

$=\frac{1}{2}(AB+BC+CA)=\frac{1}{2}.32=16$ (cm)

Vậy chu vi tam giác MNP bằng 16 cm.

Bài 4.21 trang 89 Toán 8 Tập 1: Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng

A. 4 cm.

B. 5 cm.

C. 6 cm.

D. 7 cm.

Lời giải:

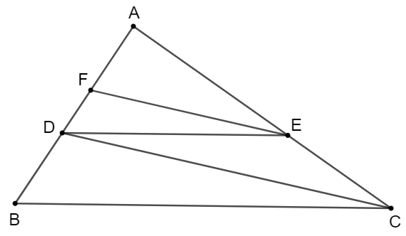
Đáp án đúng là: A

Áp dụng định lí Thalès:

• Với DE // BC (E ∈ AC) ta có: $\frac{AD}{AB}=\frac{AE}{AC}=\frac{9}{12}=\frac{2}{3}$;

• Với EF // CD (F ∈ AB) ta có: $\frac{AF}{AD}=\frac{AE}{AC}=\frac{2}{3}$.

Suy ra $AF=\frac{2}{3}AD=\frac{2}{3}.6=4$ (cm).

Vậy AF = 4 cm.

Bài 4.22 trang 89 Toán 8 Tập 1: Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là

A. 3 cm.

B. 6 cm.

C. 9 cm.

D. 12 cm.

Lời giải:

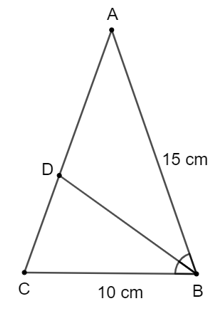
Đáp án đúng là: C

Vì tam giác ABC cân tại A nên AB = AC = 15 cm.

Theo đề bài, BD là tia phân giác của $\widehat{ABC}$, áp dụng tính chất đường phân giác vào tam giác ABC, ta có: 

$\frac{AB}{BC}=\frac{AD}{CD}=\frac{15}{10}=\frac{3}{2}$ suy ra $\frac{AD}{3}=\frac{CD}{2}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{AD}{3}=\frac{CD}{2}=\frac{AD+CD}{3+2}=\frac{AC}{5}=\frac{15}{5}=3$

Do đó AD = 3 . 3 = 9 (cm).

Vậy AD = 9 cm.

Tự luận

Bài 4.23 trang 89 Toán 8 Tập 1: Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.

Lời giải:

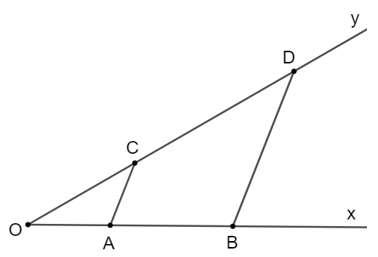
Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D hay AC // BD.

Áp dụng định lí Thalès vào tam giác OBD, ta có:

$\frac{OA}{OB}=\frac{OC}{OD}$ hay $\frac{2}{5}=\frac{3}{OD}$ .

Suy ra $OD=\frac{5.3}{2}=\mathrm{7,5}$ (cm)

Ta có OD = OC + CD suy ra CD = OD – OC = 7,5 – 3 = 4,5 (cm).

Vậy CD = 4,5 cm.

Bài 4.24 trang 89 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.

a) Chứng minh rằng AE = DF.

b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

Lời giải:

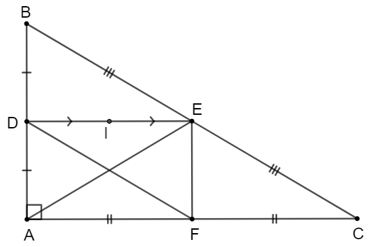
a) Theo đề bài, tam giác ABC vuông tại A nên $\widehat{BAC}=90°$ hay AB ⊥ AC.

Vì D, E lần lượt là trung điểm của AB, BC nên DE là đường trung bình của tam giác ABC suy ra DE // AC.

Mà AB ⊥ AC nên AB ⊥ DE hay $\widehat{ADE}=90°$.

Tương tự, ta chứng minh được: EF ⊥ AC hay $\widehat{AFE}=90°$.

Ta có: $\widehat{BAC}+\widehat{ADE}+\widehat{AFE}+\widehat{DEF}=360°$

$90°+90°+90°+\widehat{DEF}=360°$

$270°+\widehat{DEF}=360°$

Suy ra $\widehat{DEF}=360°-270°=90°$.

Tứ giác ADEF có $\widehat{BAC}=90°;\widehat{ADE}=90°;\widehat{AFE}=90°;\widehat{DEF}=90°$ .

Do đó tứ giác ADEF là hình chữ nhật.

Suy ra hai đường chéo AE và DF bằng nhau.

Vậy AE = DF (đpcm).

b) Vì D, F lần lượt là trung điểm của AB, AC nên DF là đường trung bình của tam giác ABC.

Suy ra DF // BC hay DF // BE.

Vì tứ giác ADEF là hình chữ nhật nên AD // EF hay BD // EF.

Tứ giác BDFE có DF // BE và BD // EF nên tứ giác BDFE là hình bình hành.

Hình bình hành BDFE có hai đường chéo BF và DE.

Mà I là trung điểm của DE nên I cũng là trung điểm của BF.

Do đó, ba điểm B, I, F thẳng hàng.

Bài 4.25 trang 89 Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.

Lời giải:

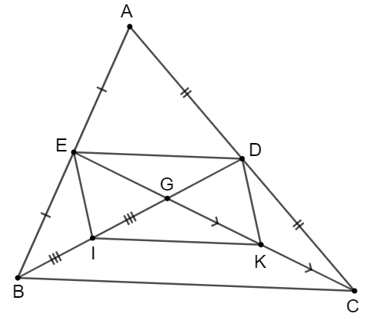
Vì BD và CE là đường trung tuyến nên E, D lần lượt là trung điểm của AB, AC.

Suy ra DE là đường trung bình của tam giác ABC.

Khi đó, DE // BC và $DE=\frac{1}{2}BC$         (1)

Vì I, K lần lượt là trung điểm của GB, GC nên IK là đường trung bình của tam giác GBC suy ra IK // BC và $IK=\frac{1}{2}BC$ (2)

Từ (1) và (2) suy ra DE // IK và $DE=IK=\frac{1}{2}BC$.

Tứ giác EDKI có DE // IK và DE = IK nên tứ giác EDKI là hình bình hành (đpcm).

Bài 4.26 trang 89 Toán 8 Tập 1: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB). Chứng minh MN song song với BC.

Lời giải:

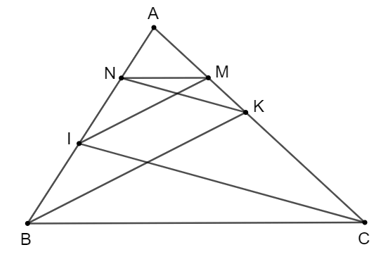
Áp dụng định lí Thalès:

• Vì IM // BK nên $\frac{AI}{AB}=\frac{AM}{AK}$  suy ra AB.AM = AI.AK          (1)

• Vì KN // IC nên $\frac{AN}{AI}=\frac{AK}{AC}$  suy ra AN.AC = AI.AK           (2)

Từ (1) và (2) suy ra AB.AM = AN.AC = AI.AK        

Do đó $\frac{AN}{AB}=\frac{AM}{AC}$  (theo tính chất tỉ lệ thức).

Suy ra MN // BC (theo định lí Thalès đảo).

Bài 4.27 trang 89 Toán 8 Tập 1: Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

Lời giải:

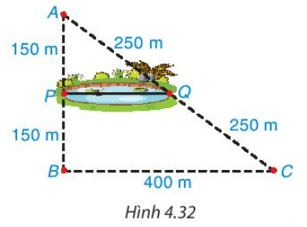
Trong Hình 4.32 có AP = BP = 150 m; AQ = CQ = 250 m.

Suy ra PQ là đường trung bình của tam giác ABC.

Do đó $PQ=\frac{1}{2}BC=\frac{1}{2}.400=200$ (m)

Vậy khoảng cách giữa hai điểm P và Q là 200 m.