Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập hai đường thẳng chéo nhau và hai đường thẳng song song lớp 11.
Giải bài tập Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
Trả lời câu hỏi giữa bài:
Lời giải:
Học sinh tự quan sát
Chẳng hạn: Mô phỏng lớp học và các cạnh tường được kí hiệu như sau:
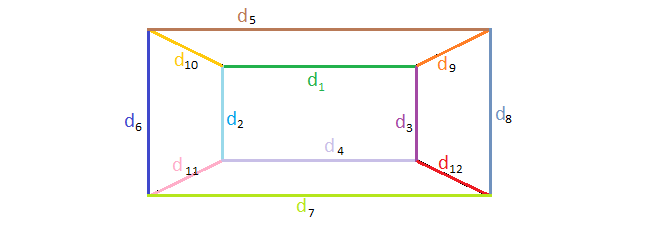
Một số cặp đường thẳng không thể cùng thuộc một mặt phẳng là:
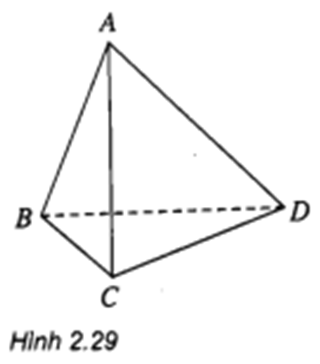
Lời giải:
Giả sử phản chứng, hai đường thẳng và không chéo nhau, nghĩa là tồn tại một mặt phẳng chứa hai đường thẳng và .
Khi đó
Hay bốn điểm đồng phẳng.
Điều này mâu thuẫn với giả thiết là tứ diện.
Vậy và chéo nhau.
Các cặp đường thẳng chéo nhau khác của tứ diện này: và , và .
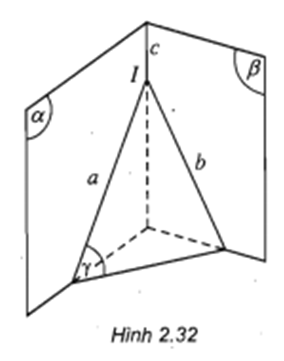
Lời giải:
và cắt nhau tại nên:
(vì là giao tuyến của và )
( vì là giao tuyến của và )
Nên là điểm chung của và .
Bài tập trang 59, 60 SGK Toán 11
a) Ba đường thẳng hoặc song song hoặc đồng quy.
b) Ba đường thẳng hoặc song song hặc đồng quy.
Phương pháp giải:
Xác định 3 mặt phẳng mà giao tuyến của chúng là để vận dụng định lí sau:
Định lí 2 (về giao tuyến của ba mặt phẳng):
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
Lời giải:
Gọi mặt phẳng qua bốn điểm là . Ta có:
hoặc đôi một song song hoặc đồng quy.
b)
Ta có:
Do đó các giao tuyến hoặc đôi một song song, hoặc đồng quy.
a) song song với ;
b) cắt .
Phương pháp giải:
Sử dụng định lí 2 (về giao tuyến của ba mặt phẳng):
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
Lời giải:
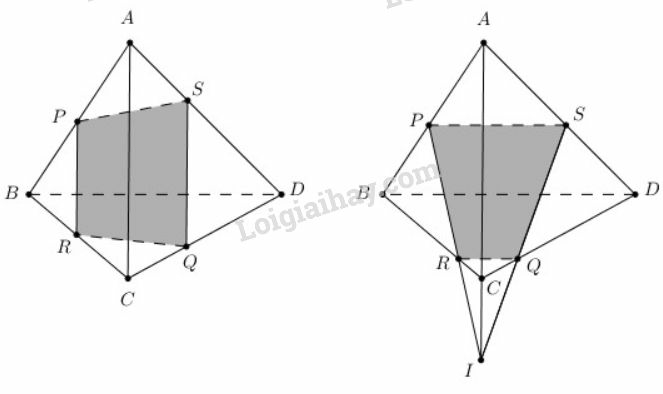
a) Ta có: .
Mà và nên hay là đường thẳng đi qua và song song .
Trong , qua kẻ đường thẳng song song với cắt tại .
Vậy .
Cách khác:
Có thể sử dụng hệ quả sau: "Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song hoặc trùng với một trong hai đường thẳng đó".
mp và mp lần lượt chứa hai đường thẳng song song .
là đường thẳng song song với và .
Gọi
.
b) Gọi là giao điểm của với .
Ta có: đồng quy tại .
Trong , kéo dài cắt tại .
Khi đó và nên .
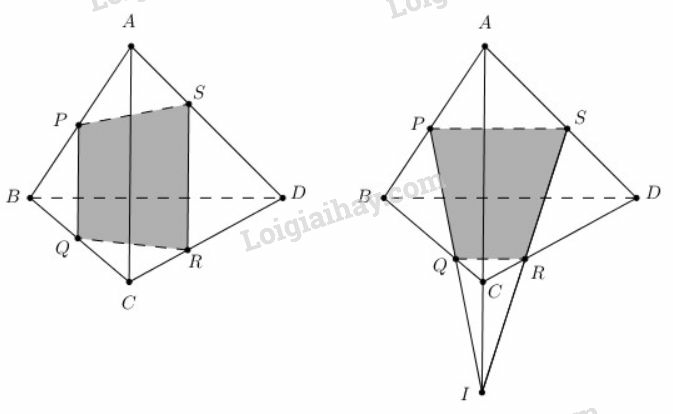
a) Tìm giao điểm của đường thẳng và mặt phẳng
b) Qua kẻ đường thẳng song song với và cắt tại . Chứng minh thẳng hàng và .
c) Chứng minh .
Phương pháp giải:
a) Trong : Gọi .
b) Sử dụng định lí đường trung bình của tam giác.
c) Sử dụng tính chất đường trung bình của tam giác.
Lời giải:
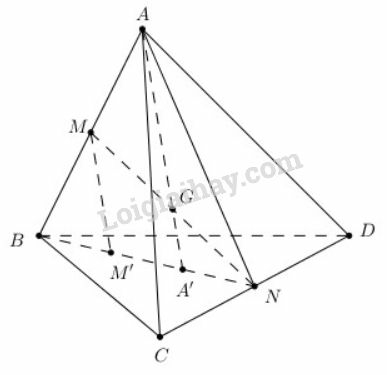
a) Có:
Trong : Gọi
.
b) Ta có:
Suy ra
.
Mà cũng thuộc nên thẳng hàng (cùng nằm trên ).
*) Xét tam giác có:
+) là trung điểm của .
+)
là trung điểm của
Xét tam giác có:
+) là trung điểm của
+)
là trung điểm của
Do đó: .
c) Ta có
Lý thuyết Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đã cho.
- Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
- Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng ( nếu có) cũng song song với hai đường thẳng đó ( hoặc trùng với một trong hai đường thẳng đó).
- Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau
Cách chứng minh hai đường thẳng và chéo nhau:
Dùng phương pháp phản chứng: Giả sử không chéo nhau - tức là và cùng nằm trong mặt phẳng , lập luận dẫn tới mâu thuẫn vậy và chéo nhau.
Cách chứng minh hai đường thẳng và song song:
Sử dụng các tính chất nêu trên hoặc đưa về một mặt phẳng rồi sử dụng các tính chất trong hình học phẳng: Tính chất hình bình hành; Đường trung bình của tam giác; Định lí Ta-let....
Trường hợp I: Hai đường thẳng đồng phẳng
Tức là hai đường thẳng cùng nằm trong một mặt phẳng.
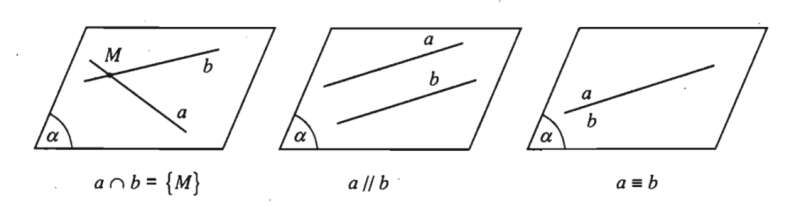
- ( và có điểm chung duy nhất.
- ( và không có đểm chung.
- ( trùng .
Trường hợp II: Hai đường thẳng chéo nhau
Tức là hai đường thẳng không cùng nằm trong một mặt phẳng hay không có mặt phẳng nào chứa hai đường thẳng đó.
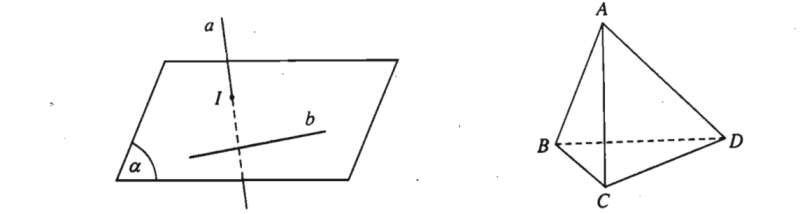
Chẳng hạn: Trong tứ diện , có 2 cặp đường thẳng chéo nhau là: và và .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.