Với giải Luyện tập 3 trang 113 Toán 11 Tập 1 Cánh Diều chi tiết trong Bài 5: Hình lăng trụ và hình hộp giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Luyện tập 3 trang 113 Toán 11 Tập 1 | Cánh Diều Giải Toán lớp 11
Luyện tập 3 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua một điểm.
Lời giải:
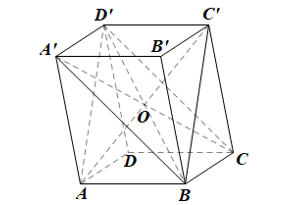
Trong mặt phẳng (ABC’D’), xét tứ giác ABC’D’ có:
AB // C’D’ (cùng song song với DC);
AB = C’D’ (cùng bằng DC)
Do đó tứ giác ABC’D’ là hình bình hành.
Suy ra hai đường chéo AC’ và BD’ cắt nhau tại trung điểm O của mỗi đường.
Khi đó (ABC’D’) đi qua điểm O.
Tương tự ta cũng có tứ giác BCD’A’ là hình bình hành có hai đường chéo BD’ và CA’ cắt nhau tại trung điểm của mỗi đường.
Mà O là trung điểm của BD’, do đó O là trung điểm của CA’ và (BCD’A’) đi qua O.
Chứng minh tương tự với các mp(CDA’B’), (DAB’C’) thì các mặt phẳng này cũng đi qua điểm O.
Vậy bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua điểm, điểm O là giao điểm các đường chéo của hình hộp.
Xem thêm các bài giải SGK Toán 11 Cánh Diều hay, chi tiết khác:
Hoạt động 3 trang 111 Toán 11 Tập 1: Vẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành.
Bài 1 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C D’. Chứng minh rằng (ACB’) // (A’C’D).
Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.