Với giải Bài 4.39 trang 102 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 4.39 trang 102 Toán 11 Tập 1 | Kết nối tri thức Giải Toán lớp 11
Bài 4.39 trang 102 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số bằng
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
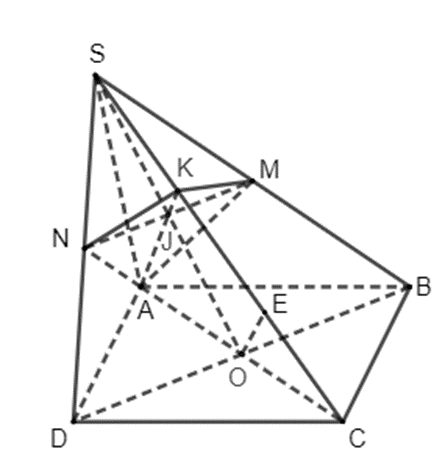
Gọi O là giao điểm hai đường chéo hình bình hành ABCD. Trong mặt phẳng (SBD), SO cắt MN tại J.
Trong mặt phẳng (SAC), AJ cắt SC tại K.
Vì J thuộc MN nên J thuộc mặt phẳng (AMN) nên K thuộc AJ thì K thuộc mặt phẳng (AMN). Do đó K là giao điểm của mặt phẳng (AMN) và đường thẳng SC.
Tam giác SBD có M, N lần lượt là trung điểm của các cạnh SB, SD nên MN là đường trung bình của tam giác SBD, suy ra MN // BD hay NJ // DO. Xét tam giác SDO có NJ // DO và N là trung điểm của SD nên suy ra J là trung điểm của SO.
Trong mặt phẳng (SAC), từ O kẻ OE song song với AK (E thuộc SC).
Xét tam giác SOE có JK // OE (do AK // OE), theo định lí Thalés ta có: .
Do đó, K là trung điểm của SE.
Xét tam giác CAK có OE // AK, theo định lí Thalés ta có: . Do đó, E là trung điểm của CK.
Vậy SK = KE = CE, suy ra .
Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 4.35 trang 102 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt mặt phẳng (P) theo giao tuyến là đường thẳng b. Vị trí tương đối của hai đường thẳng a và b là
Bài 4.36 trang 102 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Đường thẳng SB song song với mặt phẳng
Bài 4.37 trang 102 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng (AB'D') song song với mặt phẳng
Bài 4.38 trang 102 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, Cnvà đường thẳng b cắt các mặt phẳng (P), (Q), (R) lần lượt tại A', B', C'. Tỉ số bằng?
Bài 4.39 trang 102 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số bằng
Bài 4.40 trang 102 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, M' lần lượt là trung điểm của các cạnh BC, B'C'. Hình chiếu của ∆B'DM qua phép chiếu song song trên (A'B'C'D') theo phương chiếu AA' là
Bài 4.41 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:
Bài 4.42 trang 103 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA'.
Bài 4.43 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên cạnh SC và cạnh AB lần lượt lấy điểm M và N sao cho CM = 2SM và BN = 2AN.
Bài 4.44 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD.
Bài 4.45 trang 103 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm của cạnh AD, A'B'. Chứng minh rằng:
Bài 4.46 trang 103 Toán 11 Tập 1: Cho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC.
Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 13: Hai mặt phẳng song song
Bài 14: Phép chiếu song song
Bài 15: Giới hạn của dãy số
Bài 16: Giới hạn của hàm số
Bài 17: Hàm số liên tục
