Toptailieu.vn biên soạn và giới thiệu lời Toán 11 (Kết nối tri thức) Bài 17: Hàm số liên tục hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Sgk Toán 11 Bài 16 từ đó học tốt môn Toán 11.

Toán 11 (Kết nối tri thức) Bài 17: Hàm số liên tục

Giải Toán 11 trang 119

Mở đầu trang 119 Toán 11 Tập 1: Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

Lời giải:

Áp dụng định lí: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a) f(b) < 0 thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.

1. Hàm số liên tục tại một điểm

HĐ1 trang 119 Toán 11 Tập 1: Nhận biết tính liên tục của hàm số tại một điểm

Cho hàm số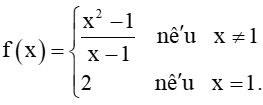 

Tìm giới hạn $\underset{x\to 1}{\lim }f\left(x\right)$ và so sánh giá trị này với f(1).

Lời giải:

Ta có: f(1) = 2.

$\underset{x\to 1}{\lim }f\left(x\right)$$=\underset{x\to 1}{\lim }\frac{x^2-1}{x-1}=\underset{x\to 1}{\lim }\frac{\left(x-1\right)\left(x+1\right)}{x-1}$$=\underset{x\to 1}{\lim }\left(x+1\right)=1+1=2$.

Vậy $\underset{x\to 1}{\lim }f\left(x\right)$ = f(1).

Giải Toán 11 trang 120

Luyện tập 1 trang 120 Toán 11 Tập 1: Xét tính liên tục của hàm số 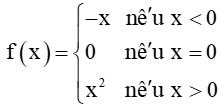 tại điểm x₀ = 0.

Lời giải:

Hàm số f(x) xác định trên ℝ, do đó x₀ = 0 thuộc tập xác định của hàm số.

Ta có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }{x}^2=0^2=0$; $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(-x\right)=0$.

Do đó, $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=0$, suy ra $\underset{x\to 0}{\lim }f\left(x\right)=0$.

Lại có f(0) = 0 nên $\underset{x\to 0}{\lim }f\left(x\right)=f\left(0\right)$. Vậy hàm số f(x) liên tục tại x₀ = 0.

2. Hàm số liên tục trên một khoảng

HĐ2 trang 120 Toán 11 Tập 1: Cho hai hàm số 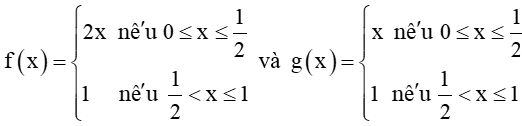 với đồ thị tương ứng như Hình 5.7.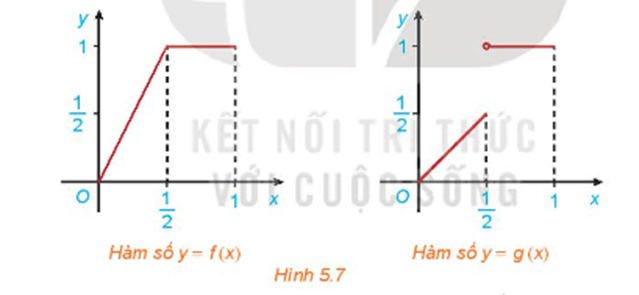

Xét tính liên tục của các hàm số f(x) và g(x) tại điểm $x=\frac{1}{2}$ và nhận xét về sự khác nhau giữa hai đồ thị.

Lời giải:

+) Hàm số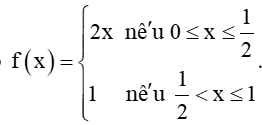 

Hàm số f(x) xác định trên [0; 1], do đó $x=\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: $\underset{x\to {\frac{1}{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{+}}{\lim }1=1$; $\underset{x\to {\frac{1}{2}}^{-}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }\left(2x\right)=2\cdot \frac{1}{2}=1$.

Suy ra $\underset{x\to {\frac{1}{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }f\left(x\right)=1$, do đó $\underset{x\to \frac{1}{2}}{\lim }f\left(x\right)=1$

Mà $f\left(\frac{1}{2}\right)=2\cdot \frac{1}{2}=1$ nên $\underset{x\to \frac{1}{2}}{\lim }f\left(x\right)=f\left(\frac{1}{2}\right)$.

Vậy hàm số f(x) liên tục tại $x=\frac{1}{2}$.

+) Hàm số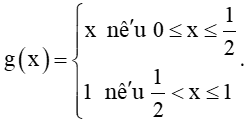 

Hàm số g(x) liên tục trên [0; 1], do đó $x=\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: $\underset{x\to {\frac{1}{2}}^{-}}{\lim }g\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }x=\frac{1}{2}$; $\underset{x\to {\frac{1}{2}}^{+}}{\lim }g\left(x\right)=\underset{x\to {\frac{1}{2}}^{+}}{\lim }1=1$

Suy ra $\underset{x\to {\frac{1}{2}}^{+}}{\lim }g\left(x\right)\ne \underset{x\to {\frac{1}{2}}^{-}}{\lim }g\left(x\right)$.

Vậy không tồn tại giới hạn của hàm số g(x) tại $x=\frac{1}{2}$, do đó hàm số g(x) gián đoạn tại $x=\frac{1}{2}$.

+) Quan sát Hình 5.7 ta thấy, đồ thị của hàm số y = f(x) là đường liền trên (0; 1), còn đồ thị của hàm số y = g(x) trên (0; 1) là các đoạn rời nhau.

Giải Toán 11 trang 121

Luyện tập 2 trang 121 Toán 11 Tập 1: Tìm các khoảng trên đó hàm số $f\left(x\right)=\frac{x^2+1}{x+2}$ liên tục.

Lời giải:

Biểu thức $\frac{x^2+1}{x+2}$ có nghĩa khi x + 2 ≠ 0 hay x ≠ – 2.

Do đó, tập xác định của hàm số f(x) là (–∞; – 2) ∪ (– 2; +∞).

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 2) và (– 2; +∞).

3. Một số tính chất cơ bản

HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x² và g(x) = – x + 1.

a) Xét tính liên tục của hai hàm số trên tại x = 1.

b) Tính  và so sánh L với f(1) + g(1).

Lời giải:

a) Hàm số f(x) = x² và g(x) = – x + 1 là các hàm đa thức nên nó liên tục trên ℝ.

Do đó, hai hàm số f(x) và g(x) đều liên tục tại x = 1.

b) Ta có: f(x) + g(x) = x² + (– x + 1) = x² – x + 1.

Do đó, $=\underset{x\to 1}{\lim }\left(x^2-x+1\right)=1^2-1+1=1$.

Lại có, f(1) = 1² = 1; g(1) = – 1 + 1 = 0, do đó f(1) + g(1) = 1 + 0 = 1.

Vậy L = f(1) + g(1) = 1.

Bài tập

Giải Toán 11 trang 122

Bài 5.14 trang 122 Toán 11 Tập 1:Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 2 và . Tính g(1).

Lời giải:

Vì hàm số f(x) liên tục tại x = 1 nên hàm số 2f(x) cũng liên tục tại x = 1.

Mà hàm số g(x) liên tục tại x = 1. Do đó, hàm số y = 2f(x) – g(x) liên tục tại x = 1.

Suy ra 

Vì  và f(1) = 2 nên ta có 3 = 2 . 2 – g(1) ⇔ g(1) = 1.

Vậy g(1) = 1.

Bài 5.15 trang 122 Toán 11 Tập 1: Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$;

b)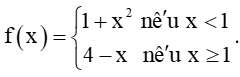 

Lời giải:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$

Biểu thức $\frac{x}{x^2+5x+6}$ có nghĩa khi x² + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0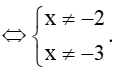 

Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).

Vì f(x) là hàm phân thức hữu tỉ nên nó liên tục trên tập xác định.

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞).

b)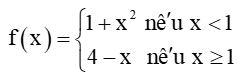 

Tập xác định của hàm số là ℝ.

+) Nếu x < 1, thì f(x) = 1 + x².

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (–∞; 1).

+) Nếu x > 1, thì f(x) = 4 – x.

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (1; +∞).

+) Ta có: $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(4-x\right)=4-1=3$;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(1+x^2\right)=1+1^2=2$.

Suy ra $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$, do đó không tồn tại giới hạn của f(x) tại x = 1.

Khi đó, hàm số f(x) không liên tục tại x = 1.

Vậy hàm số đã cho liên tục trên các khoảng (–∞; 1), (1; +∞) và gián đoạn tại x = 1.

Bài 5.16 trang 122 Toán 11 Tập 1 :Tìm giá trị của tham số m để hàm sốliên tục trên ℝ.

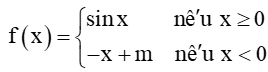
Lời giải:

Tập xác định của hàm số là ℝ.

+) Nếu x > 0, thì f(x) = sin x. Do đó nó liên tục trên (0; +∞).

+) Nếu x < 0, thì f(x) = – x + m, đây là hàm đa thức nên nó liên tục trên (–∞; 0).

Khi đó, hàm số f(x) liên tục trên các khoảng (–∞; 0) và (0; +∞).

Do đó, để hàm số f(x) liên tục trên ℝ thì f(x) phải liên tục tại x = 0. Điều này xảy ra khi và chỉ khi $\underset{x\to 0}{\lim }f\left(x\right)=f\left(0\right)$$\iff \underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=f\left(0\right)$ (1).

Lại có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\sin x=0$; f(0) = sin 0 = 0; $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(-x+m\right)=m$ .

Khi đó, (1) ⇔ m = 0.

Vậy m = 0 thì thỏa mãn yêu cầu bài toán.

Bài 5.17 trang 122 Toán 11 Tập 1: Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.

b) Xét tính liên tục của hàm số ở câu a.

Lời giải:

a) Gọi x (km, x > 0) là quãng đường khách di chuyển và y (đồng) là số tiền khách phải trả theo quãng đường di chuyển x.

Với x ≤ 0,5, ta có y = 10 000.

Với 0,5 < x ≤ 30, ta có: y = 10 000 + 13 500(x – 0,5) hay y = 13 500x + 3 250.

Với x > 30, ta có: y = 10 000 + 13 500 . 29,5 + 11 000(x – 30) hay y = 11 000x + 78 250.

Vậy công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển là

b) +) Với 0 < x < 0,5 thì y = 10 000 là hàm hằng nên nó liên tục trên (0; 0,5).

+) Với 0,5 < x < 30 thì y = 13500x + 3 250 là hàm đa thức nên nó liên tục trên (0,5; 30).

+) Với x > 30 thì y = 11 000x + 78 250 là hàm đa thức nên nó liên tục trên (30; +∞).

+) Ta xét tính liên tục của hàm số tại x = 0,5 và x = 30.

- Tại x = 0,5, ta có y(0,5) = 10 000;

$\underset{x\to 0,5^{-}}{\lim }y=\underset{x\to 0,5^{-}}{\lim }10000=10000$;

$\underset{x\to 0,5^{+}}{\lim }y=\underset{x\to 0,5^{+}}{\lim }\left(13500x+3250\right)$= 13 500 . 0,5 + 3 250 = 10 000.

Do đó, $\underset{x\to 0,5^{-}}{\lim }y=\underset{x\to 0,5^{+}}{\lim }y=\underset{x\to 0,5}{\lim }y=y\left(0,5\right)$ nên hàm số liên tục tại x = 0,5.

- Tại x = 30, ta có: y(30) = 13 500 . 30 + 3 250 = 408 250;

$\underset{x\to {30}^{-}}{\lim }y=\underset{x\to {30}^{-}}{\lim }\left(13500x+3250\right)$ = 13 500 . 30 + 3 250 = 408 250;

$\underset{x\to {30}^{+}}{\lim }y=\underset{x\to {30}^{+}}{\lim }\left(11000x+78250\right)$ = 11 000 . 30 + 78 250 = 408 250.

Do đó, $\underset{x\to {30}^{-}}{\lim }y=\underset{x\to {30}^{+}}{\lim }y=\underset{x\to 30}{\lim }y=y\left(30\right)$ nên hàm số liên tục tại x = 30.

Vậy hàm số ở câu a liên tục trên (0; +∞).

Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Một vài áp dụng của toán học trong tài chính