Với giải Bài 4.41 trang 103 Toán 11 Tập 1Kết nối tri thức chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 4.41 trang 103 Toán 11 Tập 1 | Kết nối tri thức Giải Toán lớp 11
Bài 4.41 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:
a) (SAD) và (SBC);
b) (SAB) và (SCD);
c) (SAC) và (SBD).
Lời giải:
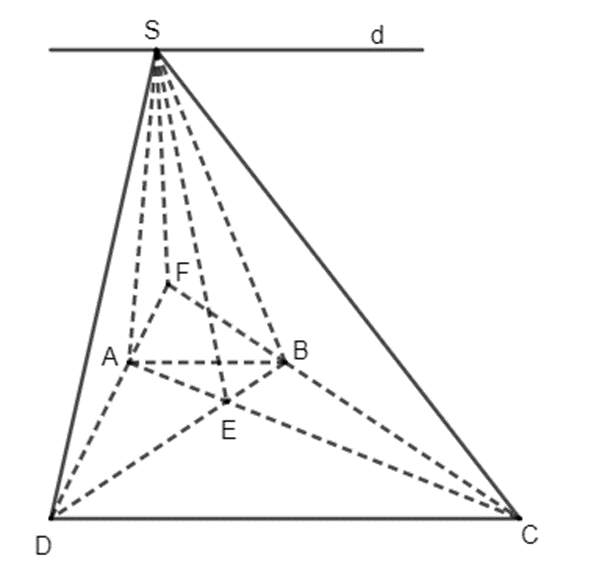
a) Ta có: ABCD là hình thang có hai đáy AB và CD. Trong mặt phẳng (ABCD), gọi F là giao điểm của AD và BC. Khi đó F thuộc AD nên F thuộc mặt phẳng (SAD), F thuộc BC nên F thuộc mặt phẳng (SBC), vậy F là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Lại có S là một điểm chung khác của hai mặt phẳng (SAD) và (SBC).
Do vây, SF là giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Hai mặt phẳng (SAB) và (SCD) lần lượt chứa hai đường thẳng AB và CD song song với nhau. Khi đó giao tuyến của hai mặt phẳng này là đường thẳng đi qua điểm chung S và song song với AB, CD.
Qua S, vẽ đường thẳng d song song với AB, CD.
Vậy d là giao tuyến của hai mặt phẳng (SAB) và (SCD).
c) Trong mặt phẳng (ABCD), gọi E là giao điểm của AC và BD. Vì E thuộc AC nên E thuộc mặt phẳng (SAC), vì E thuộc BD nên E thuộc mặt phẳng (SBD). Do vậy, E là một điểm chung của hai mặt phẳng (SAC) và (SBD).
Lại có S là một điểm chung khác của hai mặt phẳng (SAC) và (SBD).
Vậy SE là giao tuyến của hai mặt phẳng (SAC) và (SBD).
Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 4.35 trang 102 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt mặt phẳng (P) theo giao tuyến là đường thẳng b. Vị trí tương đối của hai đường thẳng a và b là
Bài 4.36 trang 102 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Đường thẳng SB song song với mặt phẳng
Bài 4.37 trang 102 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng (AB'D') song song với mặt phẳng
Bài 4.38 trang 102 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, Cnvà đường thẳng b cắt các mặt phẳng (P), (Q), (R) lần lượt tại A', B', C'. Tỉ số bằng?
Bài 4.39 trang 102 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số bằng
Bài 4.40 trang 102 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, M' lần lượt là trung điểm của các cạnh BC, B'C'. Hình chiếu của ∆B'DM qua phép chiếu song song trên (A'B'C'D') theo phương chiếu AA' là
Bài 4.41 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:
Bài 4.42 trang 103 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA'.
Bài 4.43 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên cạnh SC và cạnh AB lần lượt lấy điểm M và N sao cho CM = 2SM và BN = 2AN.
Bài 4.44 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD.
Bài 4.45 trang 103 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm của cạnh AD, A'B'. Chứng minh rằng:
Bài 4.46 trang 103 Toán 11 Tập 1: Cho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC.
Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 13: Hai mặt phẳng song song
Bài 14: Phép chiếu song song
Bài 15: Giới hạn của dãy số
Bài 16: Giới hạn của hàm số
Bài 17: Hàm số liên tục
