Toptailieu.vn biên soạn và giới thiệu lời giải Toán 11 (Chân trời sáng tạo): Bài tập cuối chương 3 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài tập cuối chương 3 từ đó học tốt môn Toán 11.

Toán 11 (Chân trời sáng tạo): Bài tập cuối chương 3

Bài tập

Giải Toán 11 trang 85 Tập 1

Bài 1 trang 85 Toán 11 Tập 1: lim$\frac{n+3}{n^2}$ bằng:

A. 1;

B. 0;

C. 3;

D. 2.

Lời giải:

Đáp án đúng là B

Ta có: $\lim \frac{n+3}{n^2}=\lim \frac{\frac{1}{n}+\frac{3}{n^2}}{1}=0$.

Bài 2 trang 85 Toán 11 Tập 1: Tổng của cấp số nhân lùi vô hạn:

$M=1+\frac{1}{4}+\frac{1}{4^2}+\mathrm{...}+\frac{1}{4^n}+\mathrm{...}$ bằng:

A. $\frac{3}{4}$;

B. $\frac{5}{4}$;

C. $\frac{4}{3}$;

D. $\frac{6}{5}$.

Lời giải:

Đáp án đúng là C

Cấp số nhân lùi vô hạn đã cho có số hạng đầu u₁ = 1 và công bội q = $\frac{1}{4}$ có tổng bằng:

$M=1+\frac{1}{4}+\frac{1}{4^2}+\mathrm{...}+\frac{1}{4^n}+\mathrm{...}=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}$.

Bài 3 trang 85 Toán 11 Tập 1: $\underset{x\to 3}{\lim }\frac{x^2-9}{x-3}$ bằng

A. 0;

B. 6;

C. 3;

D. 1.

Lời giải:

Đáp án đúng là B

Ta có: $\underset{x\to 3}{\lim }\frac{x^2-9}{x-3}=\underset{x\to 3}{\lim }\frac{\left(x+3\right)\left(x-3\right)}{x-3}=\underset{x\to 3}{\lim }\left(x+3\right)=6$.

Bài 4 trang 85 Toán 11 Tập 1: Hàm số: f(x) = 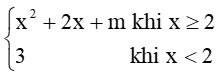 liên tục tại x = 2 khi

A. m = 3;

B. m = 5;

C. m = – 3;

D. m = – 5.

Lời giải:

Đáp án đúng là D

Ta có: $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\left(x^2+2x+m\right)=m+8$

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }3=3$

Để hàm số liên tục tại x = 2 thì m + 8 = 3 ⇔ m = – 5.

Vậy với m = – 5 thì hàm số đã cho liên tục tại x = 2.

Bài 5 trang 85 Toán 11 Tập 1: $\underset{x\to +\infty }{\lim }\frac{2x-1}{x}$ bằng

A. 2;

B. – 1;

C. 0;

D. 1.

Lời giải:

Đáp án đúng là A

Ta có: $\underset{x\to +\infty }{\lim }\frac{2x-1}{x}=\underset{x\to +\infty }{\lim }\frac{2-\frac{1}{x}}{1}=2$.

Bài tập tự luận

Giải Toán 11 trang 86 Tập 1

Bài 6 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim \frac{3n-1}{n}$;

b) $\lim \frac{\sqrt{n^2+2}}{n}$;

c) $\lim \frac{2}{3n+1}$;

d) $\lim \frac{(n+1)\left(2n+2\right)}{n^2}$.

Lời giải:

a) $\lim \frac{3n-1}{n}=\lim \frac{3-\frac{1}{n}}{1}=3$.

b) $\lim \frac{\sqrt{n^2+2}}{n}=\lim \frac{\sqrt{1+\frac{2}{n^2}}}{1}=1$.

c) $\lim \frac{2}{3n+1}=\lim \frac{\frac{2}{n}}{3+\frac{1}{n}}=0$.

d) $\lim \frac{(n+1)\left(2n+2\right)}{n^2}=\lim \frac{2n^2+4n+2}{n^2}=\lim \frac{2+\frac{4}{n}+\frac{2}{n^2}}{1}=2$.

Bài 7 trang 86 Toán 11 Tập 1: Cho tam giác đều có cạnh bằng a, gọi là tam giác H₁. Nỗi các trung điểm của H₁ để tạo thành tam giác H₂. Tiếp theo, nối các trung điểm của H₂ để tạo thành tam giác H₃ (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác H₁, H₂, H₃, ...

Tỉnh tổng chu vi và tổng diện tích của các tam giác của dãy.

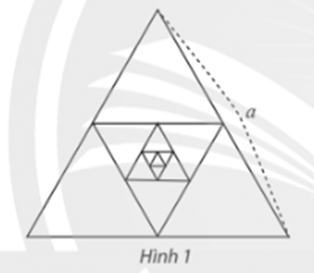
Lời giải:

Ta có:

Diện tích tam giác H₁ = S và chu vi tam giác H₁ = 3a;

Diện tích tam giác H₂ = $\frac{1}{4}$S và chu vi tam giác H₂ = $\frac{1}{2}$3a;

Diện tích tam giác H₂ = ${\left(\frac{1}{4}\right)}^2$S và chu vi tam giác H₃ = ${\left(\frac{1}{2}\right)}^2$3a;

...

Diện tích tam giác H_n = ${\left(\frac{1}{4}\right)}^{n-1}$S và chu vi tam giác H₂ = ${\left(\frac{1}{2}\right)}^{n-1}$3a;

Khi đó:

Diện tích của dãy các tam giác H₁; H₂; H₃; ...; H₄ lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u₁ = S và công bội q = $\frac{1}{4}$ có tổng bằng $S+\frac{1}{4}S+{\left(\frac{1}{4}\right)}^{2}S+\mathrm{...}+{\left(\frac{1}{4}\right)}^{n-1}S+\mathrm{...}=\frac{S}{1-\frac{1}{4}}=\frac{4}{3}S$.

Diện tích của dãy các tam giác H₁; H₂; H₃; ...; H₄ lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u₁ = 3a và công bội q = $\frac{1}{2}$ có tổng bằng

$3a+\frac{1}{2}.3a+{\left(\frac{1}{2}\right)}^2.3a+{\left(\frac{1}{2}\right)}^3.3a+\mathrm{...}+{\left(\frac{1}{2}\right)}^{n-1}3a+\mathrm{...}=\frac{3a}{1-\frac{1}{2}}=6a$.

Bài 8 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\underset{x\to -1}{\lim }\left(3x^2-x+2\right)$;

b) $\underset{x\to 4}{\lim }\frac{x^2-16}{x-4}$;

c) $\underset{x\to 2}{\lim }\frac{3-\sqrt{x+7}}{x-2}$.

Lời giải:

a) $\underset{x\to -1}{\lim }\left(3x^2-x+2\right)=6$.

b) $\underset{x\to 4}{\lim }\frac{x^2-16}{x-4}=\underset{x\to 4}{\lim }\frac{\left(x-4\right)\left(x+4\right)}{x-4}=\underset{x\to 4}{\lim }\left(x+4\right)=8$.

c) $\underset{x\to 2}{\lim }\frac{3-\sqrt{x+7}}{x-2}=\underset{x\to 2}{\lim }\frac{\left(2-x\right)\left(3+\sqrt{x+7}\right)}{x-2}=\underset{x\to 2}{\lim }\left(-3-\sqrt{x+7}\right)=-6$.

Bài 9 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\underset{x\to +\infty }{\lim }\frac{-x+2}{x+1}$;

b) $\underset{x\to -\infty }{\lim }\frac{x-2}{x^2}$.

Lời giải:

a) $\underset{x\to +\infty }{\lim }\frac{-x+2}{x+1}=\underset{x\to +\infty }{\lim }\frac{-1+\frac{2}{x}}{1+\frac{1}{x}}=-1$.

b) $\underset{x\to -\infty }{\lim }\frac{x-2}{x^2}=\underset{x\to -\infty }{\lim }\frac{\frac{1}{x}-\frac{2}{x^2}}{1}=0$.

Bài 10 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\underset{x\to 4^{+}}{\lim }\frac{1}{x-4}$;

b) $\underset{x\to 2^{+}}{\lim }\frac{x}{2-x}$.

Lời giải:

a) $\underset{x\to 4^{+}}{\lim }\frac{1}{x-4}=+\infty$.

b) $\underset{x\to 2^{+}}{\lim }\frac{x}{2-x}=\underset{x\to 2^{+}}{\lim }x.\underset{x\to 2^{+}}{\lim }\frac{1}{2-x}=+\infty$.

Bài 11 trang 86 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = .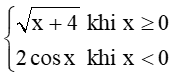

Lời giải:

+) Với x ∈ (0; + ∞) ta có f(x) = $\sqrt{x+4}$ liên tục.

+) Với x ∈ (– ∞; 0) ta có f(x) = 2cosx liên tục.

+) Tại x = 0, ta có:

$\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\sqrt{x+4}=2$;

$\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(2\cos x\right)=2$.

Suy ra $\underset{x\to 0}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=2=f\left(0\right)$

Do đó hàm số liên tục tại x = 0.

Vậy hàm số liên tục trên ℝ.

Bài 12 trang 86 Toán 11 Tập 1: Cho hàm số f(x) = 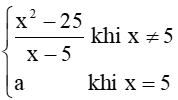. Tìm a để hàm số y = f(x) liên tục trên ℝ.

Lời giải:

+) Với mọi x ≠ 5 thì f(x) = $\frac{x^2-25}{x-5}$ liên tục.

+) Tại x = 5, ta có:

$\underset{x\to 5}{\lim }f\left(x\right)=\underset{x\to 5}{\lim }\frac{x^2-25}{x-5}=\underset{x\to 5}{\lim }\frac{\left(x-5\right)\left(x+5\right)}{x-5}=\underset{x\to 5}{\lim }\left(x+5\right)=10$.

f(5) = a

Để hàm số liên tục trên ℝ thì hàm số phải liên tục tại x = 5 khi a = 10.

Bài 13 trang 86 Toán 11 Tập 1: Trong một tủ thí nghiệm, nhiệt độ trong tủ sấy được điều khiển tăng từ 10°C, mỗi phút tăng 2°C trong 60 phút, sau đó giảm mỗi phút 3°C trong 40 phút. Hàm số biểu thị nhiệt độ (tính theo ºC) trong tủ theo thời gian t (tính theo phút) có dạng

T(t) = 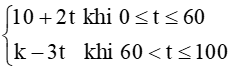 (k là hằng số).

Biết rằng T(t) là hàm liên tục trên tập xác đinh. Tìm giá trị của k.

Lời giải:

+) Với 0 ≤ t < 60 thì T(t) = 10 + 2t là hàm số liên tục.

+) Với 60 < t ≤ 100 thì T(t) = k – 3t là hàm số liên tục.

+) Tại t = 60, ta có:

$\underset{t\to {60}^{-}}{\lim }T\left(t\right)=\underset{t\to {60}^{-}}{\lim }\left(10+2t\right)=130$

$\underset{t\to {60}^{+}}{\lim }T\left(t\right)=\underset{t\to {60}^{-}}{\lim }\left(k-3t\right)=k-180$

Để hàm số liên tục trên tập xác định [0; 100] thì hàm số liên tục tại x = 60

⇔ k – 180 = 130

⇔ k = 240.

Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục