Với giải Bài 7 trang 86 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 3 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 7 trang 86 Toán 11 Tập 1 | Chân trời sáng tạo Giải Toán lớp 11
Bài 7 trang 86 Toán 11 Tập 1: Cho tam giác đều có cạnh bằng a, gọi là tam giác H1. Nỗi các trung điểm của H1 để tạo thành tam giác H2. Tiếp theo, nối các trung điểm của H2 để tạo thành tam giác H3 (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác H1, H2, H3, ...
Tỉnh tổng chu vi và tổng diện tích của các tam giác của dãy.
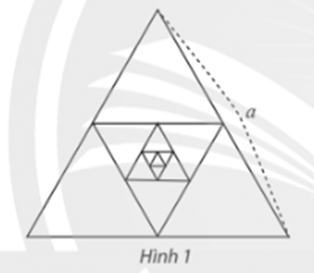
Lời giải:
Ta có:
Diện tích tam giác H1 = S và chu vi tam giác H1 = 3a;
Diện tích tam giác H2 = 14S và chu vi tam giác H2 = 123a;
Diện tích tam giác H2 = (14)2S và chu vi tam giác H3 = (12)23a;
...
Diện tích tam giác Hn = (14)n−1S và chu vi tam giác H2 = (12)n−13a;
Khi đó:
Diện tích của dãy các tam giác H1; H2; H3; ...; H4 lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u1 = S và công bội q = 14 có tổng bằng S+14S+(14)2S+...+(14)n−1S+...=S1−14=43S.
Diện tích của dãy các tam giác H1; H2; H3; ...; H4 lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u1 = 3a và công bội q = 12 có tổng bằng
3a+12.3a+(12)2.3a+(12)3.3a+...+(12)n−13a+...=3a1−12=6a.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 85 Toán 11 Tập 1: limn+3n2 bằng:
Bài 2 trang 85 Toán 11 Tập 1: Tổng của cấp số nhân lùi vô hạn: M=1+14+142+...+14n+... bằng:
Bài 3 trang 85 Toán 11 Tập 1: limx→3x2−9x−3 bằng
Bài 4 trang 85 Toán 11 Tập 1: Hàm số: f(x) = 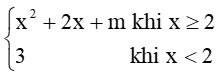 liên tục tại x = 2 khi
liên tục tại x = 2 khi
Bài 5 trang 85 Toán 11 Tập 1: limx→+∞2x−1x bằng
Bài 6 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) lim3n−1n;
Bài 8 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) limx→−1(3x2−x+2);
Bài 9 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau: a) limx→+∞−x+2x+1;
Bài 10 trang 86 Toán 11 Tập 1: Tìm các giới hạn sau:a) limx→4+1x−4;
Bài 11 trang 86 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = 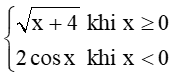 .
.
Bài 12 trang 86 Toán 11 Tập 1: Cho hàm số f(x) = 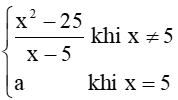 . Tìm a để hàm số y = f(x) liên tục trên ℝ.
. Tìm a để hàm số y = f(x) liên tục trên ℝ.
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.