Với giải SGK Toán 11 Chân trời sáng tạo trang 79 chi tiết trong Bài 2: Giới hạn của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 79 Tập 1 (Chân trời sáng tạo)
Bài 1 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:
a) ;
b) ;
c) .
Lời giải:
a)
.
b)
c)
.
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 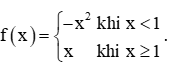 .
.
Tìm các giới hạn sau: (nếu có).
Lời giải:
+) Với dãy số (xn) bất kì, xn ≤ 1 và xn → 1. Khi đó f(xn) = nên limf(xn) = .
Vì vậy .
+) Với dãy số (xn) bất kì, xn > 1 và xn → 1. Khi đó f(xn) = xn nên limf(xn) = lim(xn) = 1.
Vì vậy .
+) Vì nên không tồn tại .
Bài 3 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:
a) ;
b) ;
c).
Lời giải:
a) .
b) .
c) .
Bài 4 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:
a) ;
b) ;
c) .
Lời giải:
a) ;
b) Ta viết:
Ta có:
Do đó: .
c) Ta viết:
Ta có:
Do đó: .
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là (gam/lít).
b) Nồng độ muối như thế nào nếu t → +∞.
Lời giải:
a) Sau t phút số lít nước biển bơm vào là: 15t (lít).
Khi đó số gam muối trong 15t lít nước biển là: 30.15t (gam).
Tổng số lít nước trong hồ là: 6000 + 15t (lít).
Nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là: (gam/lít).
b) Khi t → +∞ thì .
Vậy nồng độ muối trong hồ gần đến 30gam/lít khi t → +∞.
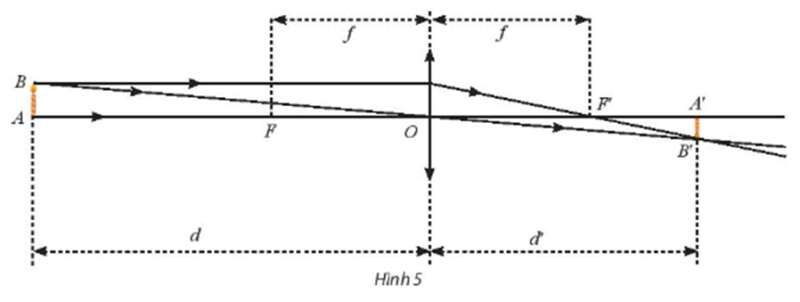
Xét hàm số . Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) ;
b) .
Lời giải:
a) Ta có: .
Như vậy khi khoảng cách của vật đến quang tâm O gần bằng tiêu cự của thấu kính thì khoảng cách từ ảnh đến quang tâm O của thấu kính càng lớn.
b) Ta có: .
Như vậy khi khoảng cách của vật đến quang tâm O càng lớn thì khoảng cách từ ảnh đến quang tâm O của thấu kính càng gần tiêu cự.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 71 Toán 11 Tập 1: Xét hàm số
Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;
Thực hành 2 trang 73 Toán 11 Tập 1:Tìm các giới hạn sau: a) ;
Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số 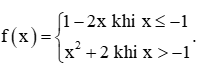
Thực hành 4 trang 76 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;
Hoạt động khám phá 5 trang 77 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 4.
Thực hành 5 trang 78 Toán 11 Tập 1: Tìm các giới hạn sau: a) ; b) .
Bài 1 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau: a) ;
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 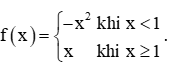 .
.
Bài 3 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:a) ; b) ;
Bài 4 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:a) ; b) ;
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.