Với giải Bài 4 trang 99 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 4 trang 99 Toán 11 Tập 1 | Chân trời sáng tạo Giải Toán lớp 11
Bài 4 trang 99 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D).
a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) và (ACD).
b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Lời giải:
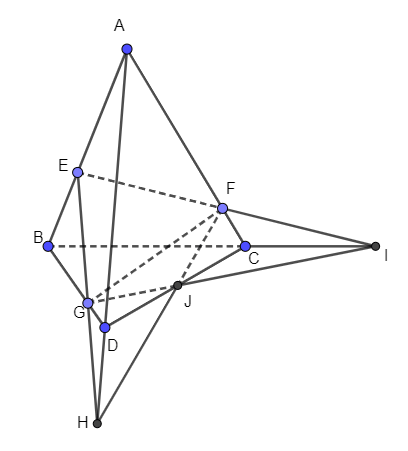
a) +) Ta có: EF ∩ BC = {I}, EG ∩ BD = {G}
Mà EF, EG ⊂ (EGF) và BC, BD ⊂ (BCD)
Suy ra (EFG) ∩ (BCD) = {IG}.
+) Ta có: EF ∩ AC = {F}, EG ∩ AD = {H}
Mà EF, EG ⊂ (EGF) và AC, AD ⊂ (ACD)
Suy ra (EFG) ∩ (ACD) = {FH}.
b) Ta có: 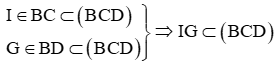
Mà CD ⊂ (BCD)
Gọi J là giao điểm của IG và CD.
Ta lại có: 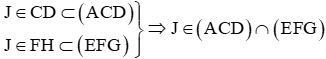
Mặt khác: (ACD) ∩ (EFG) = IG
Do đó J ∈ IG.
Vậy ba đường thẳng CD, IG, HF cùng đi qua điểm J.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 89 Toán 11 Tập 1: a) Vẽ hình biểu diễn của một hình hộp chữ nhật.
Thực hành 3 trang 90 Toán 11 Tập 1: Có bao nhiêu mặt phẳng đi qua ba đỉnh của tam giác MNP?
Hoạt động khám phá 11 trang 97 Toán 11 Tập 1: Trong Hình 34, hình chóp nào có số mặt ít nhất?
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.