Mở đầu trang 9 Chuyên đề Toán 11: Khi diễu hành, để đội hình được giữ vững, ở mỗi bước, những người tham gia cần tiến đều nhau về cùng một hướng. Điều này có gì liên quan tới Toán học?

Lời giải:

Nhắc đến hướng và độ dài (đều nhau), có nghĩa là nhắc đến khái niệm vectơ, một nội dung kiến thức trong Toán học. Vậy khi diễu hành, để đội hình được giữ vững, những người tham gia cần vận dụng một số kiến thức về Toán học.

1. Phép tịnh tiến

HĐ1 trang 9 Chuyên đề Toán 11: Ở mỗi bước của đội hình diễu hành, gọi vectơ dịch chuyển của mỗi người tham gia là vectơ có điểm gốc và điểm ngọn tương ứng là vị trí trước và sau khi bước của người đó. Để giữ vững đội hình, ở mỗi bước, các vectơ dịch chuyển của những người tham gia cần có mối quan hệ gì với nhau? 

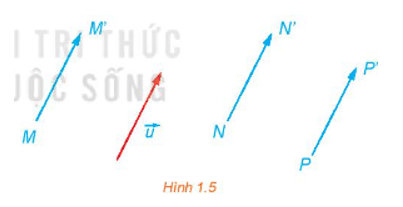
Lời giải:

Để giữa vững đội hình, ở mỗi bước, các vectơ dịch chuyển của những người tham gia cần có cùng phương, cùng hướng và có độ dài bằng nhau hay các vectơ dịch chuyển này phải bằng nhau.

Câu hỏi trang 9 Chuyên đề Toán 11: Nếu phép tịnh tiến $T_{\overrightarrow{u}}$ biến điểm M thành điểm M' thì phép tịnh tiến $T_{\overrightarrow{\mathrm{-u}}}$ biến điểm M' thành điểm nào?

Lời giải:

Phép tịnh tiến $T_{\overrightarrow{u}}$ biến điểm M thành M' thì $\overrightarrow{MM\text{'}}=\overrightarrow{u}$.

Suy ra $-\overrightarrow{u}=-\overrightarrow{MM\text{'}}=\overrightarrow{M\text{'}M}$.

Do đó, phép tịnh tiến $T_{\overrightarrow{\mathrm{-u}}}$ biến điểm M' thành điểm M.

Luyện tập 1 trang 10 Chuyên đề Toán 11: Trong Hình 1.6, tìm ảnh của các điểm M, N, P, Q, B qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$.

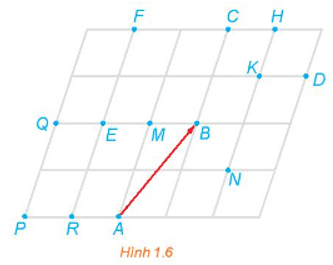
Lời giải:

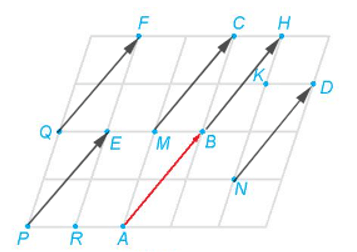
Ta có: $\overrightarrow{MC}=\overrightarrow{AB}$ nên ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$ là điểm C.

$\overrightarrow{ND}=\overrightarrow{AB}$ nên ảnh của điểm N qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$ là điểm D.

$\overrightarrow{PE}=\overrightarrow{AB}$ nên ảnh của điểm P qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$ là điểm E.

$\overrightarrow{QF}=\overrightarrow{AB}$ nên ảnh của điểm Q qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$ là điểm F.

$\overrightarrow{BH}=\overrightarrow{AB}$ nên ảnh của điểm B qua phép tịnh tiến theo vectơ $\overrightarrow{AB}$ là điểm H.

Vận dụng 1 trang 10 Chuyên đề Toán 11: Bạn Hùng tham gia vào một khối diễu hành, mỗi bước Hùng tiến về hướng đông 30 cm. Để giữ vững đội hình, sau mỗi bước, tất cả mọi người tham gia trong khối diễu hành của Hùng cần dời tới vị trí mới là ảnh của vị trí cũ qua phép biến hình nào?

Lời giải:

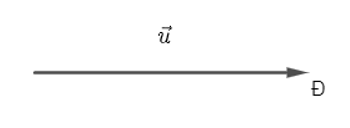
Để giữ vững đội hình, sau mỗi bước, tất cả mọi người tham gia trong khối diễu hành của Hùng cần dời tới vị trí mới là ảnh của vị trí cũ qua phép tịnh tiến theo vectơ $\overrightarrow{u}$ với vectơ $\overrightarrow{u}$ có hướng theo hướng đông và có độ dài $\left|\overrightarrow{u}\right|=30$ cm.

2. Tính chất

HĐ2 trang 10 Chuyên đề Toán 11: Phép tịnh tiến biến $T_{\overrightarrow{u}}$ biến M thành M', N thành N' (H.1.7).

a) Có nhận xét gì về $\overrightarrow{MM\text{'}}+\overrightarrow{M\text{'}M}$ và $\overrightarrow{M\text{'}N}+\overrightarrow{NN\text{'}}$.

b) Tìm mối quan hệ giữa hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{M\text{'}N\text{'}}$.

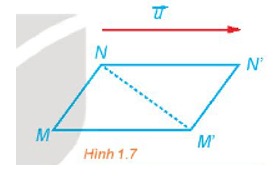
Lời giải:

a) Phép tịnh tiến $T_{\overrightarrow{u}}$ biến điểm M thành M' thì $\overrightarrow{MM\text{'}}=\overrightarrow{u}$ và biến N thành N' thì $\overrightarrow{NN\text{'}}=\overrightarrow{u}$.

Ta có: $\overrightarrow{MM\text{'}}+\overrightarrow{M\text{'}N}=\overrightarrow{u}+\overrightarrow{M\text{'}N}$ và $\overrightarrow{M\text{'}N}+\overrightarrow{NN\text{'}}=\overrightarrow{M\text{'}N}+\overrightarrow{u}$.

Do đó, $\overrightarrow{MM\text{'}}+\overrightarrow{M\text{'}N}=\overrightarrow{M\text{'}N}+\overrightarrow{NN\text{'}}$.

b) Theo quy tắc ba điểm ta có: $\overrightarrow{MN}=\overrightarrow{MM\text{'}}+\overrightarrow{M\text{'}N}$ và $\overrightarrow{M\text{'}N\text{'}}=\overrightarrow{M\text{'}N}+\overrightarrow{NN\text{'}}$.

Mà theo câu a) ta có: $\overrightarrow{MM\text{'}}+\overrightarrow{M\text{'}N}=\overrightarrow{M\text{'}N}+\overrightarrow{NN\text{'}}$.

Do đó, $\overrightarrow{MN}=\overrightarrow{M\text{'}N\text{'}}$.

Luyện tập 2 trang 11 Chuyên đề Toán 11: Cho đường tròn (O; R) và điểm O' khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O', M không thẳng hàng, vẽ hình bình hành MOO'M'. Hỏi khi M thay đổi trên (O; R) thì M' thay đổi trên đường nào?

Lời giải:

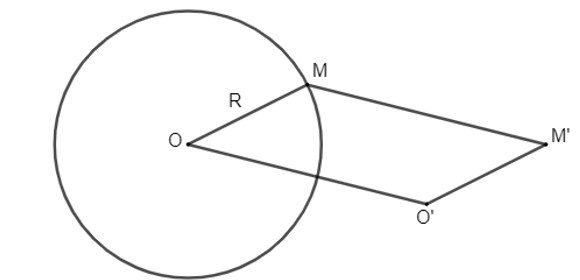
Ta có: MOO'M' là hình bình hành nên $\overrightarrow{OM}=\overrightarrow{O\text{'}M\text{'}}$ và $\overrightarrow{OO\text{'}}=\overrightarrow{MM\text{'}}$.

Vì OM = R nên $O\text{'}M\text{'}=\left|\overrightarrow{O\text{'}M\text{'}}\right|=\left|\overrightarrow{OM}\right|=OM=R$, R cố định nên O' luôn cách M' một khoảng không đổi bằng R.

Do O, O' cố định và $\overrightarrow{OO\text{'}}=\overrightarrow{MM\text{'}}$ nên phép tịnh tiến theo vectơ $\overrightarrow{OO\text{'}}$ biến điểm M thành điểm M'. Suy ra nếu M thay đổi trên (O; R) thì M' luôn là ảnh của điểm M qua phép tịnh tiến theo vectơ $\overrightarrow{OO\text{'}}$.

Lại có phép tịnh tiến theo vectơ $\overrightarrow{OO\text{'}}$ biến đường tròn (O; R) thành đường tròn có bán kính là R và có tâm là ảnh của tâm O qua phép tịnh tiến theo vectơ $\overrightarrow{OO\text{'}}$ hay chính là điểm O'. Điều này có nghĩa là đường tròn (O'; R) là ảnh của đường tròn (O; R) qua phép tịnh tiến theo vectơ $\overrightarrow{OO\text{'}}$.

Mà O'M' = R không đổi nên M' luôn thuộc đường tròn (O'; R).

Vậy khi M thay đổi trên (O; R) thì M' thay đổi trên đường tròn (O'; R) là ảnh của (O; R) qua phép tịnh tiến theo vectơ $\overrightarrow{OO\text{'}}$.

Vận dụng 2 trang 11 Chuyên đề Toán 11: Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ $\overrightarrow{u}$ có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không?

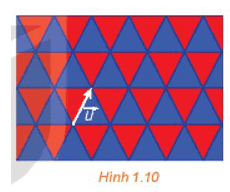
Lời giải:

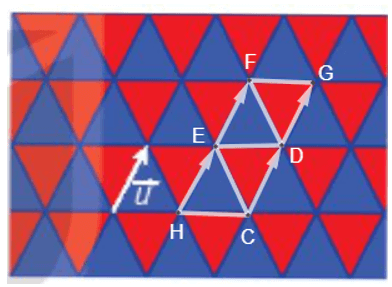
Đặt một số điểm như hình vẽ.

Ta thấy: $\overrightarrow{HE}=\overrightarrow{u},\overrightarrow{CD}=\overrightarrow{u},\overrightarrow{EF}=\overrightarrow{u}$ nên phép tịnh tiến $T_{\overrightarrow{u}}$ biến các điểm H, C, E tương ứng thành E, D, F. Do đó, $T_{\overrightarrow{u}}$ biến tam giác HCE thành tam giác EDF hay phép tịnh tiến theo vectơ $\overrightarrow{u}$ biến một viên gạch màu xanh thành một viên gạch màu xanh. Đối với các viên gạch màu xanh khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ $\overrightarrow{u}$ biến mỗi viên gạch màu xanh thành một viên gạch màu xanh.

Ta cũng có: $\overrightarrow{CD}=\overrightarrow{u},\overrightarrow{DG}=\overrightarrow{u},\overrightarrow{EF}=\overrightarrow{u}$ nên phép tịnh tiến $T_{\overrightarrow{u}}$ biến các điểm C, D, E tương ứng thành D, G, F. Do đó, $T_{\overrightarrow{u}}$ biến tam giác CDE thành tam giác DGF hay phép tịnh tiến theo vectơ $\overrightarrow{u}$ biến một viên gạch màu đỏ thành một viên gạch màu đỏ. Đối với các viên gạch màu đỏ khác, thực hiện tương tự. Vậy phép tịnh tiến theo vectơ $\overrightarrow{u}$ biến mỗi viên gạch màu đỏ thành một viên gạch màu đỏ.

Bài tập

Bài 1.3 trang 11 Chuyên đề Toán 11: Cho $\overrightarrow{u}$ là một vectơ chỉ phương của đường thẳng ∆. Hỏi phép tịnh tiến $T_{\overrightarrow{u}}$ biến ∆ thành đường thẳng nào?

Lời giải:

Vì $\overrightarrow{u}$ là vectơ chỉ phương của đường thẳng ∆ nên giá của vectơ $\overrightarrow{u}$ song song hoặc trùng với đường thẳng ∆.

Lấy điểm M bất kì thuộc đường thẳng ∆, gọi M' là ảnh của M qua phép tịnh tiến $T_{\overrightarrow{u}}$. Khi đó $\overrightarrow{MM\text{'}}=\overrightarrow{u}$.

Do đó, vectơ $\overrightarrow{MM\text{'}}$ có giá là đường thẳng MM' phải song song hoặc trùng với đường thẳng ∆, mà M ∈ ∆ nên hai đường thẳng MM' và ∆ trùng nhau hay M' ∈ ∆.

Vậy phép tịnh tiến $T_{\overrightarrow{u}}$ biến mỗi điểm M thuộc ∆ thành điểm M' cũng thuộc ∆ hay phép tịnh tiến $T_{\overrightarrow{u}}$ biến ∆ thành chính nó.

Bài 1.4 trang 11 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 1)² + (y + 2)² = 25 và vectơ $\overrightarrow{u}=\left(3;4\right)$.

a) Xác định ảnh của tâm đường tròn (C) qua phép tịnh tiến $T_{\overrightarrow{u}}$

b) Viết phương trình đường tròn (C') là ảnh của (C) qua $T_{\overrightarrow{u}}$.

Lời giải:

Ta có (C): (x – 1)² + (y + 2)² = 25 hay (x – 1)² + [y – (– 2)]² = 5².

Suy ra đường tròn (C) có tâm I(1; – 2) và bán kính R = 5.

a) Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ $\overrightarrow{u}=\left(3;4\right)$ là một đường tròn bán kính bằng 5, gọi là (C').

Gọi I' là tâm của (C'). Ta có I' là ảnh của I qua phép tịnh tiến theo vectơ $\overrightarrow{u}$ nên $\overrightarrow{II\text{'}}=\overrightarrow{u}=\left(3;4\right)$. Suy ra I'(4; 2). Vậy ảnh của (C) là đường tròn (C') có tâm I'(4; 2) và bán kính bằng 5.

b) Ta có (C'): (x – 4)² + (y – 2)² = 25.

Bài 1.5 trang 11 Chuyên đề Toán 11: Trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vectơ nào? (Gợi ý: Tính vectơ tịnh tiến đó theo hai vectơ $\overrightarrow{u},\overrightarrow{v}$ trên hình vẽ).

Lời giải:

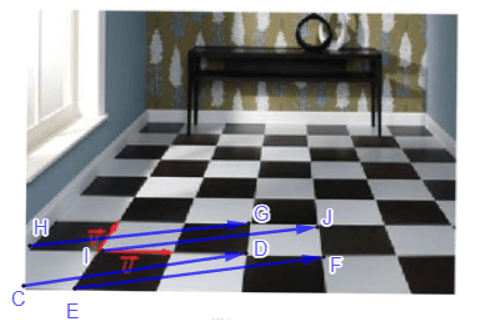
Đặt các điểm như hình vẽ trên. Viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là viên gạch GDFJ, viên gạch ở góc dưới bên trái là viên gạch HCEI.

Theo quy tắc hình bình hành, ta suy ra $\overrightarrow{IJ}=\overrightarrow{v}+3\overrightarrow{u}$. Đặt $\overrightarrow{x}=\overrightarrow{v}+3\overrightarrow{u}$.

Phép tịnh tiến $T_{\overrightarrow{x}}$ biến các điểm H, C, E, I tương ứng thành các điểm G, D, F, J. Do đó, phép tịnh tiến $T_{\overrightarrow{x}}$ biến viên gạch HCEI thành viên gạch GDFJ.

Vậy trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vectơ $\overrightarrow{x}$ với $\overrightarrow{x}=\overrightarrow{v}+3\overrightarrow{u}$.