Với giải Thực hành 1 trang 38 Chuyên đề Toán 11 Chân trời sáng tạo chi tiết trong Bài tập cuối chuyên đề 1 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:
Cho trước ba số thực a, b, k. Hãy chứng minh g là một phép đồng dạng.
Thực hành 1 trang 38 Chuyên đề Toán 11: Cho trước ba số thực a, b, k. Trong mặt phẳng tọa độ Oxy, xét phép biến hình g biến điểm M(x; y) thành điểm M’(x’; y’) thỏa mãn: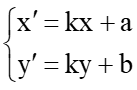 
. Hãy chứng minh g là một phép đồng dạng.
Lời giải:
Xét hai điểm bất kì M(x1; y1), N(x2; y2) có ảnh qua g lần lượt là M’(kx1 + a; ky1 + b), N’(kx2 + a; ky2 + b).
Ta có ;
Và .
.
Do đó
Vì vậy .
Suy ra M’N’ = |k|.MN.
Vậy g là phép đồng dạng tỉ số |k|.
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Vận dụng 1 trang 39 Chuyên đề Toán 11: Tìm phép đồng dạng biến hình (A) thành hình (C).
Vận dụng 2 trang 40 Chuyên đề Toán 11: Tìm các cặp hình đồng dạng với nhau có trong Hình 5.
Bài 4 trang 40 Chuyên đề Toán 11: Tìm các hình đồng dạng với nhau trong Hình 6.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
