Chứng minh rằng với mọi góc a (0độ <= a <= 180độ), ta đều có

Với giải Bài 5 trang 65 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1. Giá trị lượng giác của một góc từ 0 đến 180 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Chứng minh rằng với mọi góc a (0⁰ $\leq$ a $\leq$ 180⁰), ta đều có

Bài 5 trang 65 Toán 10 Tập 1: Chứng minh rằng với mọi góc $α (0^{o} \leq α \leq 180^{o})$ , ta đều có:

Lời giải a

a) $\cos^{2} α + \sin^{2} α = 1$

Phương pháp giải:

Lấy điểm M trên nửa đường tròn đơn vị sao cho $α = \hat{x O M}$

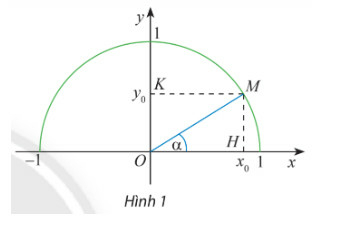
Bài 5 trang 65 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

$\sin α = \frac{M H}{O M}; \cos α = \frac{O H}{O M}; \tan α = \frac{\sin α}{\cos α}; \cot α = \frac{\cos α}{\sin α} .$

Lời giải

Trên nửa đường tròn đơn vị, lấy điểm M sao cho $\hat{x O M} = α$

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

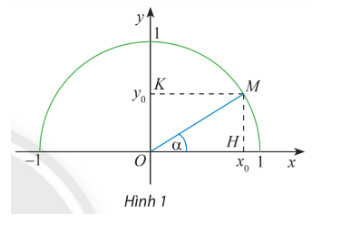
Bài 5 trang 65 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Ta có: tam giác vuông OHM vuông tại H và $α = \hat{x O M}$

Do đó: $\sin α = \frac{M H}{O M} = M H; \cos α = \frac{O H}{O M} = O H .$

$\Rightarrow \cos^{2} α + \sin^{2} α = O H^{2} + M H^{2} = O M^{2} = 1$

Lời giải b

b) $\tan α . \cot α = 1 (0^{o} < α < 180^{o}, α \neq 90^{o})$

Lời giải

Ta có:

$\begin{array}{l} \tan α = \frac{\sin α}{\cos α}; \cot α = \frac{\cos α}{\sin α} . \\ \Rightarrow \tan α . \cot α = \frac{\sin α}{\cos α} . \frac{\cos α}{\sin α} = 1 \end{array}$

Lời giải c

c) $1 + \tan^{2} α = \frac{1}{\cos^{2} α} (α \neq 90^{o})$

Lời giải

Với $α \neq 90^{o}$ ta có:

$\begin{array}{l} \tan α = \frac{\sin α}{\cos α}; \\ \Rightarrow 1 + \tan^{2} α = 1 + \frac{\sin^{2} α}{\cos^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\cos^{2} α} = \frac{1}{\cos^{2} α} \end{array}$

Lời giải d

d) $1 + \cot^{2} α = \frac{1}{\sin^{2} α} (0^{o} < α < 180^{o})$

Lời giải

Ta có:

$\begin{array}{l} \cot α = \frac{\cos α}{\sin α}; \\ \Rightarrow 1 + \cot^{2} α = 1 + \frac{\cos^{2} α}{\sin^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\sin^{2} α} = \frac{1}{\sin^{2} α} \end{array}$