Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 3: Phương trình đưa về dạng ax + b = 0

Dương Kiều Ninh Ngày: 25-05-2022 Lớp 8

670

Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 3: Phương trình đưa về dạng ax + b = 0 trang 9,10,11,12,13 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón chờ xem.

Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 3: Phương trình đưa về dạng ax + b = 0

Câu hỏi Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 :

Câu 6. Tìm từ thích hợp để điền vào chỗ trống:

a) Nếu sau khi rút gọn, phương trình cuối có dạng $0 x = 0$ thì phương trình đã cho .........

b) Nếu sau khi rút gọn, phương trình cuối có dạng $0 x = m$ , trong đó $m$ là số khác $0$ , thì phương trình đã cho .................

Phương pháp giải:

Sử dụng: Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm của bất phương trình đó.

Lời giải:

a) Nếu sau khi rút gọn, phương trình cuối có dạng $0 x = 0$ thì phương trình đã cho nghiệm đúng với mọi x.

b) Nếu sau khi rút gọn, phương trình cuối có dạng $0 x = m$ , trong đó $m$ là số khác $0$ , thì phương trình đã cho vô nghiệm.

Câu 7. Phương trình $5 x + 3 - x = 7 - 2 x$ tương đương với phương trình:

$\begin{array}{l} (A) 5 x - x + 2 x = 7 + 3 \\ (B) 5 x - x - 2 x = 7 + 3 \\ (C) 5 x - x + 2 x = 7 - 3 \\ (D) 5 x - x - 2 x = 7 - 3 \end{array}$

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp giải:

Sử dụng:

- Quy tắc chuyển vế: Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

Lời giải:

Ta có:

$\begin{array}{l} 5 x + 3 - x = 7 - 2 x \\ \Leftrightarrow 5 x - x + 2 x = 7 - 3 \end{array}$

Chọn C.

Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 7: Giải các phương trình:

a, 3x - 2 = 2x - 3

b, 3 - 4u + 24 + 6u = u + 27 + 3u

c, 5 - (x - 6) = 4(3 - 2x)

d, -6(1,5 - 2x) = 3(- 15 + 2x)

e, 0,1 - 2(0,5t - 0,1) = 2(t - 2,5) - 0,7

\frac{3}{2}

(x -

\frac{5}{4}

) -

\frac{5}{8}

= x

Phương pháp giải:

a, Thực hiện quy tắc chuyển vế các hạng tử để đưa phương trình về dạng

a x + b = 0

hoặc

a x = - b

b, Thực hiện quy tắc chuyển vế các hạng tử để đưa phương trình về dạng

a x + b = 0

hoặc

a x = - b

c,Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng

a x + b = 0

hoặc

a x = - b

d,Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng

a x + b = 0

hoặc

a x = - b

e,Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng

a x + b = 0

hoặc

a x = - b

f, Thực hiện các bước sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

Lời giải:

a, $3 x - 2 = 2 x - 3$

$\Leftrightarrow 3 x - 2 x = - 3 + 2$

$\Leftrightarrow x = - 1$

Vậy phương trình có nghiệm duy nhất $x = - 1.$

3 - 4 u + 24 + 6 u = u + 27 + 3 u

$\Leftrightarrow 2 u + 27 = 4 u + 27$

$\Leftrightarrow 2 u - 4 u = 27 - 27$

$\Leftrightarrow - 2 u = 0$

$\Leftrightarrow u = 0$

Vậy phương trình có nghiệm duy nhất $u = 0.$

5 - (x - 6) = 4 (3 - 2 x)

$\Leftrightarrow 5 - x + 6 = 12 - 8 x$

$\Leftrightarrow - x + 11 = 12 - 8 x$

$\Leftrightarrow - x + 8 x = 12 - 11$

$\Leftrightarrow 7 x = 1$

$\Leftrightarrow x = \frac{1}{7}$

Vậy phương trình có nghiệm duy nhất $x = \frac{1}{7}$ .

- 6 (1, 5 - 2 x) = 3 (- 15 + 2 x)

$\Leftrightarrow - 9 + 12 x = - 45 + 6 x$

$\Leftrightarrow 12 x - 6 x = - 45 + 9$

$\Leftrightarrow 6 x = - 36$

$\Leftrightarrow x = - 36 : 6$

$\Leftrightarrow x = - 6$

Vậy phương trình có nghiệm duy nhất $x = - 6$ .

0, 1 - 2 (0, 5 t - 0, 1) = 2 (t - 2, 5)

- 0, 7

$\Leftrightarrow 0, 1 - t + 0, 2 = 2 t - 5 - 0, 7$

$\Leftrightarrow - t + 0, 3 = 2 t - 5, 7$

$\Leftrightarrow - t - 2 t = - 5, 7 - 0, 3$

$\Leftrightarrow - 3 t = - 6$

$\Leftrightarrow t = (- 6) : (- 3)$

$\Leftrightarrow t = 2$

Vậy phương trình có nghiệm duy nhất $t = 2$

\frac{3}{2} (x - \frac{5}{4}) - \frac{5}{8} = x

$\Leftrightarrow \frac{3}{2} x - \frac{15}{8} - \frac{5}{8} = x$

$\Leftrightarrow \frac{3}{2} x - x = \frac{15}{8} + \frac{5}{8}$

$\Leftrightarrow \frac{1}{2} x = \frac{20}{8}$

$\Leftrightarrow x = \frac{20}{8} : \frac{1}{2}$

$\Leftrightarrow x = 5$

Vậy phương trình có nghiệm duy nhất $x = 5$ .

Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 8: Giải các phương trình:

a, $\frac{5 x - 2}{3}$ = $\frac{5 - 3 x}{2}$

b, $\frac{10 x + 3}{12}$ = 1 + $\frac{6 + 8 x}{2}$

c, $\frac{7 x + 1}{6}$ + 2x = $\frac{16 - x}{5}$

d, 4(0,5 - 1,5x) = - $\frac{5 x - 6}{3}$

Phương pháp giải:

a, Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế phương trình và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm nghiệm của phương trình dạng $a x + b = 0$

b, Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế phương trình và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm nghiệm của phương trình dạng $a x + b = 0$

c, Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế phương trình và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm nghiệm của phương trình dạng $a x + b = 0$

d, Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế phương trình và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm nghiệm của phương trình dạng $a x + b = 0$

Lời giải:

a, $\frac{5 x - 2}{3} = \frac{5 - 3 x}{2}$

$\Leftrightarrow \frac{2 (5 x - 2)}{6} = \frac{3 (5 - 3 x)}{6}$

$\Leftrightarrow 2 (5 x - 2) = 3 (5 - 3 x)$

$\Leftrightarrow 10 x - 4 = 15 - 9 x$

$\Leftrightarrow 10 x + 9 x = 15 + 4$

$\Leftrightarrow 19 x = 19$

$\Leftrightarrow x = 19 : 19$

$\Leftrightarrow x = 1$

Vậy phương trình có nghiệm duy nhất $x = 1$ .

\frac{10 x + 3}{12} = 1 + \frac{6 + 8 x}{9}

$\Leftrightarrow \frac{3 (10 x + 3)}{36} = \frac{36}{36} + \frac{4 (6 + 8 x)}{36}$

$\Leftrightarrow 30 x + 9 = 36 + 24 + 32 x$

$\Leftrightarrow 30 x - 32 x = 60 - 9$

$\Leftrightarrow - 2 x = 51$

$\Leftrightarrow x = \frac{- 51}{2}$

$\Leftrightarrow x = - 25, 5$

Vậy phương trình có nghiệm duy nhất $x = - 25, 5$ .

\frac{7 x - 1}{6} + 2 x = \frac{16 - x}{5}

$\Leftrightarrow \frac{5. (7 x - 1)}{30} + \frac{30.2 x}{30} = \frac{6. (16 - x)}{30}$

$\Leftrightarrow 5. (7 x - 1) + 60 x = 6 (16 - x)$

$\Leftrightarrow 35 x - 5 + 60 x = 96 - 6 x$

$\Leftrightarrow 95 x - 5 = 96 - 6 x$

$\Leftrightarrow 95 x + 6 x = 96 + 5$

$\Leftrightarrow 101 x = 101$

$\Leftrightarrow x = 101 : 101$

$\Leftrightarrow x = 1$

Vậy phương trình có nghiệm duy nhất $x = 1$ .

4 (0, 5 - 1, 5 x) = - \frac{5 x - 6}{3}

$\Leftrightarrow 2 - 6 x = - \frac{5 x - 6}{3}$

$\Leftrightarrow \frac{3 (2 - 6 x)}{3} = - \frac{5 x - 6}{3}$

$\Leftrightarrow 3 (2 - 6 x) = - (5 x - 6)$

$\Leftrightarrow 6 - 18 x = - 5 x + 6$

$\Leftrightarrow - 18 x + 5 x = 6 - 6$

$\Leftrightarrow - 13 x = 0$

$\Leftrightarrow x = 0 : (- 13)$

$\Leftrightarrow x = 0$

Vậy phương trình có nghiệm duy nhất $x = 0.$

Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 9: Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình $32$ km/h. Sau đó $1$ giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình $48$ km/h. Hãy viết phương trình biểu thị việc ô tô gặp xe máy sau $x$ giờ, kể từ khi ô tô khởi hành.

Phương pháp giải:

Áp dụng công thức: $S = v t$

Trong đó: $S$ là quãng đường đi được trong thời gian $t$ ,

$v$ là vận tốc,

$t$ là thời gian.

Lời giải:

Sự kiện ô tô gặp xe máy sau $x$ giờ có nghĩa là quãng đường ô tô đi được sau $x$ giờ và quãng đường xe máy đi được sau $x + 1$ giờ là như nhau.

Do ô tô khởi hành muộn hơn xe máy $1$ giờ nên ta có bảng sau:

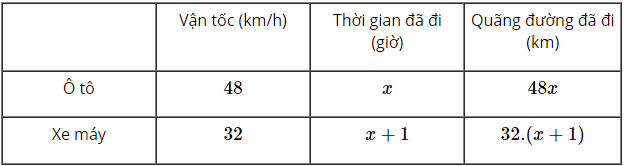
Vở bài tập Toán 8 Bài 3: Phương trình đưa về dạng ax + b = 0 (ảnh 1)

Vậy phương trình cần tìm là

48 x = 32 (x + 1) .

Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 10: Viết phương trình biểu thị cân thăng bằng trong hình vẽ bên (đơn vị khối lượng là gam).

Vở bài tập Toán 8 Bài 3: Phương trình đưa về dạng ax + b = 0 (ảnh 2)

Phương pháp giải:

- Biểu thị theo $x$ khối lượng mỗi bên của cân.

- Vì cân thăng bằng nên khối lượng bên vế trái = vế phải. Do đó, ta có phương trình cần tìm.

Lời giải:

Khối lượng trên đĩa cân bên trái là $3 x + 5$ (gam)

Khối lượng trên đĩa cân bên phải là $2 x + 7$ (gam)

Phương trình cần tìm là $3 x + 5 = 2 x + 7$ .

Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 12:Giải các phương trình:

a, $\frac{x}{3} - \frac{2 x + 1}{2} = \frac{x}{6} - x$
b, $\frac{2 + x}{5} - 0, 5 x = \frac{1 - 2 x}{4} + 0, 25$
Phương pháp giải:

a, Các bước thực hiện giải phương trình đưa về dạng $a x + b = 0$

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm nghiệm của phương trình dạng $a x + b = 0$

b, Các bước thực hiện giải phương trình đưa về dạng

a x + b = 0

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm nghiệm của phương trình dạng $a x + b = 0$

Lời giải:

$\begin{aligned} \frac{x}{3} - \frac{2 x + 1}{2} = \frac{x}{6} - x \\ \Leftrightarrow \frac{2 x - 3. (2 x + 1)}{6} = \frac{x - 6 x}{6} \\ \Leftrightarrow 2 x - 3 (2 x + 1) = x - 6 x \\ \begin{matrix} \Leftrightarrow 2 x - 6 x - 3 = - 5 x \\ \Leftrightarrow - 4 x + 5 x = 3 \\ \Leftrightarrow x = 3 \end{matrix} \end{aligned}$

Vậy phương trình có nghiệm $x = 3$ .

$\frac{2 + x}{5} - 0, 5 x = \frac{1 - 2 x}{4} + 0, 25$

$\Leftrightarrow \frac{4 (2 + x)}{20} - \frac{10 x}{20} = \frac{5 (1 - 2 x)}{20}$ $+ \frac{5}{20}$

$\Leftrightarrow 4 (2 + x) - 10 x = 5 (1 - 2 x) + 5$

$\begin{matrix} \Leftrightarrow 8 + 4 x - 10 x = 5 - 10 x + 5 \\ \Leftrightarrow 4 x - 10 x + 10 x = 5 + 5 - 8 \\ \begin{matrix} \Leftrightarrow 4 x = 2 \\ \Leftrightarrow x = \frac{2}{4} \\ \Leftrightarrow x = \frac{1}{2} \end{matrix} \end{matrix}$

Vậy phương trình có nghiệm $x = \frac{1}{2}$ .

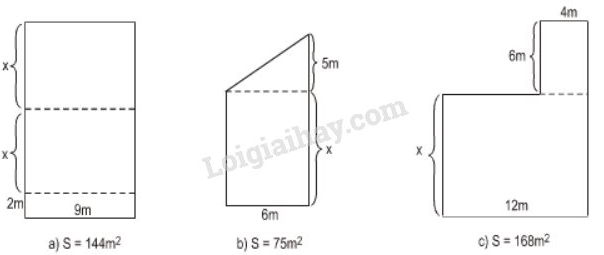
Vở bài tập Toán 8 trang 9, 10, 11, 12, 13 Bài 13: Viết phương trình ẩn x rồi tính x (mét) trong mỗi hình dưới đây (S là diện tích của hình).

Vở bài tập Toán 8 Bài 3: Phương trình đưa về dạng ax + b = 0 (ảnh 3)

Phương pháp giải:

a, Công thức tính diện tích hình chữ nhật: $S = a \times b$

Trong đó: $S$ là diện tích hình chữ nhật

$a$ là chiều dài hình chữ nhật

$b$ là chiều rộng hình chữ nhật

- Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm $x$

b, Công thức tính diện tích hình chữ nhật: $S = a \times b$

Trong đó: $S$ là diện tích hình chữ nhật

$a$ là chiều dài hình chữ nhật

$b$ là chiều rộng hình chữ nhật

Công thức tính diện tích tam giác $S = \frac{1}{2} a . h$

$a$ là cạnh của tam giác, $h$ là chiều cao tương ứng với cạnh $a$ của tam giác.

- Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm $x$

c, Công thức tính diện tích hình chữ nhật: $S = a \times b$

Trong đó: $S$ là diện tích hình chữ nhật

$a$ là chiều dài hình chữ nhật

$b$ là chiều rộng hình chữ nhật

- Để giải các phương trình đưa được về $a x + b = 0$ ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng $a x + b = 0$ hoặc $a x = - b$ .

+ Tìm $x$

Lời giải:

S = 144

(m^{2})

đúng bằng tổng diện tích của ba hình chữ nhật.

Từ đó ta có phương trình $9.2 + 9. x + 9. x = 144$

Giải phương trình này, ta được $x = 7 (m)$

Chú ý: $9.2 + 9. x + 9. x = 144$

$\Leftrightarrow 18 x + 18 = 144$

$\Leftrightarrow 18 x = 144 - 18$

$\Leftrightarrow 18 x = 126$

$\Leftrightarrow x = 126 : 18$

$\Leftrightarrow x = 7$

S = 75

(m^{2})

đúng bằng tổng diện tích của hình chữ nhật và hình tam giác.

Từ đó ta có phương trình $6. x + \frac{1}{2} .6 .5 = 75$

Giải phương trình này, ta được $x = 10 (m)$ .

Chú ý: $6. x + \frac{1}{2} .6 .5 = 75$

$\begin{array}{l} \Leftrightarrow 6 x + 15 = 75 \\ \Leftrightarrow 6 x = 75 - 15 \\ \Leftrightarrow 6 x = 60 \\ \Leftrightarrow x = 60 : 6 \\ \Leftrightarrow x = 10 \end{array}$

S = 168

(m^{2})

đúng bằng tổng diện tích của hai hình chữ nhật.

Từ đó ta có phương trình $12. x + 4.6 = 168$

Giải phương trình này, ta được $x = 12 (m) .$

Chú ý: $12. x + 4.6 = 168$

$12 x + 24 = 168$

$\Leftrightarrow 12 x = 168 - 24$

$\Leftrightarrow 12 x = 144$

$\Leftrightarrow x = 144 : 12$

$\Leftrightarrow x = 12$

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

227

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

286

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

236