Vở bài tập Toán 8 trang 7, 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải.

Dương Kiều Ninh Ngày: 25-05-2022 Lớp 8

509

Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 7, 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.

Vở bài tập Toán 8 trang 7, 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải

Câu hỏi Vở bài tập Toán 8 trang 7, 8:

Câu 4. Tìm từ thích hợp điền vào chỗ trống trong mệnh đề sau:

Từ một phương trình, dùng quy tắc chuyển vế hay quy tắc nhân, ta luôn nhận được một phương trình mới ........ với phương trình đã cho.

Phương pháp giải:

Sử dụng lí thuyết phương trình bậc nhất một ẩn và cách giải.

Lời giải:

Từ một phương trình, dùng quy tắc chuyển vế hay quy tắc nhân, ta luôn nhận được một phương trình mới tương đương với phương trình đã cho.

Câu 5. Đúng ghi Đ, sai ghi S vào ô trống trong mỗi khẳng định sau đây.

a) Nếu chuyển vế một hạng tử trong một phương trình, mà quên không đổi dấu hạng tử đó thì phương trình nhận được không tương đương với phương trình bạn đầu. $◻$

b) Nếu nhân cả hai vế của một phương trình với $0$ thì ta được phương trình mới tương đương với phương trình ban đầu. $◻$

c) Nếu bỏ đi hai hạng tử như nhau ở hai vế của một phương trình thì được phương trình mới tương đương với phương trình ban đầu. $◻$

Phương pháp giải:

Sử dụng lí thuyết phương trình bậc nhất một ẩn và cách giải.

Lời giải:

a, Đ

b, S

c, Đ

Vở bài tập Toán 8 trang 7, 8 Bài 4: Tính diện tích của hình thang ABCD theo x bằng hai cách:

1) Tính theo công thức S = BH X (BC + DA) : 2

2) S = $S_{A B H}$ + $S_{B C K H} + S_{C K D}$

Sau đó sử dụng giả thiết để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

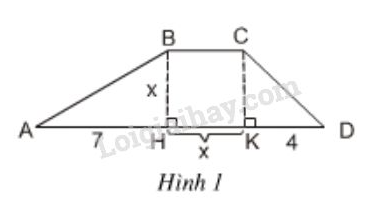
VBT Toán 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải. (ảnh 1)

Phương pháp giải:

Phương trình có dạng

a x + b = 0

, với

a

và

b

là hai số đã cho và

a \neq 0

, được gọi là phương trình bậc nhất một ẩn.
Lời giải:

1) Theo công thức $S = B H \times (B C + D A) : 2$

Ta có: $D A = 7 + x + 4 = 11 + x$ , $B C = x$ , $B H = x$ .

Vậy

$S = x (x + 11 + x) : 2$ $= x (11 + 2 x) : 2 = \frac{11 x + 2 x^{2}}{2}$

Ta có phương trình: $\frac{11 x + 2 x^{2}}{2} = 20$ (1)

2) Theo công thức $S = S_{A B H} + S_{B C K H} + S_{C K D}$

Ta có: $S_{A B H} = \frac{1}{2} B H . A H = \frac{1}{2} x .7 = \frac{7}{2} x$ ; $S_{B C K H} = B H . H K = x . x = x^{2}$ ; $S_{C K D} = \frac{1}{2} C K . K D = \frac{1}{2} . x .4 = 2 x$

$S = \frac{7}{2} x + x^{2} + 2 x$

Ta có phương trình $\frac{7}{2} x + x^{2} + 2 x = 20$ (2)

Trong hai phương trình trên, không có phương trình nào là phương trình bậc nhất.

Vở bài tập Toán 8 trang 7, 8 Bài 5: Giải các phương trình:

a, 4x - 20 = 0

b, 2x + x +12 = 0

c, x - 5 = 3 - x

d, 7 - 3x = 9 - x

Phương pháp giải:

a, Phương trình ax + b = 0 (với a ‡ 0) được giải như sau:

ax + b = 0 ⇔ ax = -b ⇔ x =

\frac{- b}{a}

Vậy phương trình có một nghiệm duy nhất là

x = \frac{- b}{a}

+) Quy tắc chuyển vế

Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

+) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân (hoặc chia) cả hai vế phương trình với cùng một số khác $0$ .

+) Quy tắc chuyển vế

Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

+) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân (hoặc chia) cả hai vế phương trình với cùng một số khác $0$ .

+) Quy tắc chuyển vế

Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

+) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân (hoặc chia) cả hai vế phương trình với cùng một số khác $0$ .

Lời giải:
a,

$4 x - 20 = 0$

$\Leftrightarrow 4 x = 20$

$\Leftrightarrow x = 20 : 4$

$\Leftrightarrow x = 5$

Vậy tập nghiệm của phương trình là $S = {5} .$

$2 x + x + 12 = 0$

$\Leftrightarrow 3 x + 12 = 0$

$\Leftrightarrow 3 x = - 12$

$\Leftrightarrow x = (- 12) : 3$

$\Leftrightarrow x = - 4$

Vậy tập nghiệm của phương trình là $S = {- 4} .$

$x - 5 = 3 - x$

$\Leftrightarrow x + x = 3 + 5$

$\Leftrightarrow 2 x = 8$

$\Leftrightarrow x = 8 : 2$

$\Leftrightarrow x = 4$

Vậy tập nghiệm của phương trình là $S = {4} .$

$7 - 3 x = 9 - x$

$\Leftrightarrow - 3 x + x = 9 - 7$

$\Leftrightarrow - 2 x = 2$

$\Leftrightarrow x = 2 : (- 2)$

$\Leftrightarrow x = - 1$

Vậy tập nghiệm của phương trình là $S = {- 1} .$

Vở bài tập Toán 8 trang 7, 8 Bài 6: Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm:

3 x - 11 = 0

;

12 + 7 x = 0

;

10 - 4 x = 2 x - 3

Phương pháp giải:

Phương trình $a x + b = 0$ (với $a \neq 0$ ) được giải như sau:

$a x + b = 0 \Leftrightarrow a x = - b \Leftrightarrow x = \frac{- b}{a}$

Vậy phương trình có một nghiệm duy nhất là $x = \frac{- b}{a}$

Phương trình $a x + b = 0$ (với $a \neq 0$ ) được giải như sau:

$a x + b = 0 \Leftrightarrow a x = - b \Leftrightarrow x = \frac{- b}{a}$

Vậy phương trình có một nghiệm duy nhất là $x = \frac{- b}{a}$

+) Quy tắc chuyển vế

Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

+) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân (hoặc chia) cả hai vế phương trình với cùng một số khác $0$ .

Lời giải:

$3 x - 11 = 0$

$\Leftrightarrow 3 x = 11$

$\Leftrightarrow x = \frac{11}{3}$

Mặt khác $\frac{11}{3} = 3, 6666...$

Vậy giá trị gần đúng của nghiệm là $x \approx 3, 67$ .

$12 + 7 x = 0$

$\Leftrightarrow 7 x = - 12$

$\Leftrightarrow x = \frac{- 12}{7}$

Mặt khác $\frac{- 12}{7} = - 1, 71428...$

Vậy giá trị gần đúng của nghiệm là $x \approx - 1, 71$

$10 - 4 x = 2 x - 3$

$\Leftrightarrow - 4 x - 2 x = - 3 - 10$

$\Leftrightarrow - 6 x = - 13$

$\Leftrightarrow x = \frac{- 13}{- 6}$

$\Leftrightarrow x = \frac{13}{6}$

Mặt khác $\frac{13}{6} = 2, 166...$

Vậy giá trị gần đúng của nghiệm là $x \approx 2, 17$ .

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương