Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 5: Phương trình chứa ẩn ở mẫu

Dương Kiều Ninh Ngày: 26-05-2022 Lớp 8

530

Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 5 : Phương trình chứa ẩn ở mẫu chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.

Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 5: Phương trình chứa ẩn ở mẫu

Câu hỏi Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23: Đúng ghi Đ, sai gh S vào ô trống trong mỗi khẳng định sau đây.

a) Sau khi quy đồng mẫu thức hai vế của một phương trình, ta được phương trình mới tương đương với phương trình đã cho. $◻$

b) Sau khi khử mẫu thức trong một phương trình, ta được phương trình mới tương đương với phương trình đã cho $◻$

Phương pháp giải:

Sử dụng lí thuyết về phương trình chứa ẩn ở mẫu.
Lời giải:

a) Đ.

b) S.

(Khi khử mẫu ta được phương trình mới không tương đương với phương trình đã cho, do đó khi giải ra nghiệm ta phải kiểm tra xem nghiệm có thỏa mãn ĐKXĐ của phương trình không mới kết luận).

Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 18: Giải các phương trình:

Câu 1

a, $\frac{2 x - 5}{x + 5}$ = 3

b, $\frac{x^{2} - 6}{x} = x + \frac{3}{2}$

c, $\frac{(x^{2} + 2 x) - (3 x + 6)}{x - 3} = 0$ ;

d, $\frac{5}{3 x + 2} = 2 x - 1$

Phương pháp giải:

a, Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Lời giải:

a, Điều kiện xác định: $x \neq - 5$

Quy đồng mẫu thức hai vế:

$\frac{2 x - 5}{x + 5} = \frac{3 (x + 5)}{x + 5}$

Khử mẫu thức:

$2 x - 5 = 3 (x + 5)$

Giải phương trình nhận được:

$2 x - 5 = 3 x + 15$ $\Leftrightarrow 2 x - 3 x = 15 + 5$

$\Leftrightarrow - x = 20 \Leftrightarrow x = - 20$

Kiểm tra kết quả:

Giá trị $x = - 20$ thỏa mãn điều kiện $x \neq - 5$ .

Kết luận:

Vậy tập nghiệm của phương trình là: $S = {- 20}$ .

Điều kiện xác định: $x \neq 0$

Quy đồng mẫu thức hai vế:

$\frac{2 (x^{2} - 6)}{2 x} = \frac{2 x^{2} + 3 x}{2 x}$

Khử mẫu thức:

$2 (x^{2} - 6) = 2 x^{2} + 3 x$

Giải phương trình nhận được:

$2 x^{2} - 12 = 2 x^{2} + 3 x$

$\Leftrightarrow 2 x^{2} - 2 x^{2} - 3 x = 12$

$\Leftrightarrow - 3 x = 12$

$\Leftrightarrow x = 12 : (- 3) = - 4$

Kiểm tra kết quả:

Giá trị $x = - 4$ thỏa mãn điều kiện $x \neq 0$

Kết luận:

Vậy tập nghiệm của phương trình là: $S = {- 4}$

Điều kiện xác định: $x \neq 3$

Quy đồng mẫu thức hai vế:

$\frac{(x^{2} + 2 x) - (3 x + 6)}{x - 3} = \frac{0}{x - 3}$

Khử mẫu thức:

$(x^{2} + 2 x) - (3 x + 6) = 0$

Giải phương trình nhận được:

$x (x + 2) - 3 (x + 2) = 0$

$\Leftrightarrow (x + 2) (x - 3) = 0$

$\Leftrightarrow x + 2 = 0$ hoặc $x - 3 = 0$

$\Leftrightarrow x = - 2$ hoặc $x = 3$

Kiểm tra kết quả:

Giá trị $x = - 2$ thỏa mãn điều kiện $x \neq 3$

Giá trị $x = 3$ không thỏa mãn điều kiện $x \neq 3$ .

Kết luận:

Vậy tập nghiệm của phương trình là: $S = {- 2}$

Điều kiện xác định: $x \neq - \frac{2}{3}$

Quy đồng mẫu thức hai vế:

$\frac{5}{3 x + 2} = \frac{(2 x - 1) (3 x + 2)}{3 x + 2}$

Khử mẫu thức:

$5 = (2 x - 1) (3 x + 2)$

Giải phương trình nhận được:

$- 6 x^{2} - x + 2 + 5 = 0$

$\Leftrightarrow - 6 x^{2} - x + 7 = 0$

$\Leftrightarrow - 6 x^{2} + 6 x - 7 x + 7 = 0$

$\Leftrightarrow - 6 x (x - 1) - 7 (x - 1) = 0$

$\Leftrightarrow (x - 1) (- 6 x - 7) = 0$

$\Leftrightarrow x - 1 = 0$ hoặc $- 6 x - 7 = 0$

$\Leftrightarrow x = 1$ hoặc $x = - \frac{7}{6}$

Kiểm tra kết quả:

Giá trị $x = 1$ thỏa mãn điều kiện $x \neq - \frac{2}{3}$ .

Giá trị $x = - \frac{7}{6}$ thỏa mãn điều kiện $x \neq - \frac{2}{3}$ .

Kết luận:

Vậy tập nghiệm của phương trình là: $S = {1; - \frac{7}{6}}$

Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 19: Giải các phương trình:

\frac{2 x - 1}{x - 1}

+ 1 =

\frac{1}{x - 1}

\frac{5 x}{2 x + 2} + 1 = - \frac{6}{x + 1}

x + \frac{1}{x} = x^{2} + \frac{1}{x^{2}}

;

\frac{x + 3}{x + 1} + \frac{x - 2}{x} = 2

Phương pháp giải:

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Kết luận.

Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thỏa mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.

Lời giải:

Điều kiện xác định: $x - 1 \neq 0$ , tức là $x \neq 1$ .

Quy đồng mẫu thức: $\frac{2 x - 1}{x - 1} + 1 = \frac{1}{x - 1}$

$\Leftrightarrow \frac{2 x - 1}{x - 1} + \frac{x - 1}{x - 1} = \frac{1}{x - 1}$

Khử mẫu thức, ta được phương trình: $2 x - 1 + x - 1 = 1$

Giải phương trình ta được:

$3 x - 2 = 1 \Leftrightarrow 3 x = 3 \Leftrightarrow x = 1$

Kiểm tra kết quả: Giá trị $x = 1$ không thỏa mãn điều kiên xác định.

Kết luận: Vậy phương trình vô nghiệm.

Điều kiện xác định: $2 x + 2 \neq 0$ , tức là $x \neq - 1$ .

Quy đồng mẫu thức: $\frac{5 x}{2 (x + 1)} + \frac{2 x + 2}{2 (x + 1)} = - \frac{6.2}{2 (x + 1)}$

Khử mẫu thức, ta được phương trình: $5 x + 2 x + 2 = - 12$

Giải phương trình ta được:

$7 x = - 14 \Leftrightarrow x = - 14 : 7 = - 2$

Kiểm tra kết quả: Giá trị $x = - 2$ thỏa mãn điều kiên xác định.

Kết luận: Vậy phương trình có nghiệm $x = - 2$ .

Điều kiện xác định: $x \neq 0$ .

Quy đồng mẫu thức: $\frac{x^{3}}{x^{2}} + \frac{x}{x^{2}} = \frac{x^{4}}{x^{2}} + \frac{1}{x^{2}}$

Khử mẫu thức, ta được phương trình: $x^{3} + x = x^{4} + 1$ (1)

Giải phương trình (1):

$\begin{array}{l} (1) \Leftrightarrow x^{4} - x^{3} - x + 1 = 0 \\ \Leftrightarrow x^{3} (x - 1) - (x - 1) = 0 \\ \Leftrightarrow (x - 1) (x^{3} - 1) = 0 \\ \Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x^{3} - 1 = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} x = 1 \\ x^{3} = 1 \end{array} \\ \Leftrightarrow x = 1 \end{array}$

Kiểm tra kết quả: Giá trị $x = 1$ thỏa mãn điều kiên xác định

Kết luận: Vậy phương trình có nghiệm duy nhất

x = 1

Điều kiện xác định: $x + 1 \neq 0; x \neq 0$ , tức là $x \neq 0; x \neq - 1$ .

Quy đồng mẫu thức:

$\frac{x (x + 3)}{x (x + 1)} + \frac{(x - 2) (x + 1)}{x (x + 1)}$ $= \frac{2 x (x + 1)}{x (x + 1)}$

Khử mẫu thức, ta được phương trình:

$x (x + 3) + (x - 2) (x + 1)$ $= 2 x (x + 1)$ (2)

Giải phương trình (2):

$\Leftrightarrow x^{2} + 3 x + x^{2} - 2 x + x - 2$ $= 2 x^{2} + 2 x$

$\Leftrightarrow 2 x^{2} + 2 x - 2 - 2 x^{2} - 2 x = 0$

$\Leftrightarrow 0 x = 2$ (vô nghiệm).

Kết luận: Vậy phương trình đã cho vô nghiệm.

Bài 20 trang 20 VBT Toán 8 tập 2: Giải các phương trình:
a,

\frac{1}{x - 2} + 3 = \frac{x - 3}{2 - x}

2 x - \frac{2 x^{2}}{x + 3} = \frac{4 x}{x + 3} + \frac{2}{7}

\frac{x + 1}{x - 1} - \frac{x - 1}{x + 1} = \frac{4}{x^{2} - 1}

\frac{3 x - 2}{x + 7} = \frac{6 x + 1}{2 x - 3}

Phương pháp giải:

Tìm điều kiện xác định.

- Qui đồng khử mẫu.

- Giải phương trình bằng cách chuyển vế.

- Tìm điều kiện xác định.

- Qui đồng khử mẫu.

- Giải phương trình bằng cách chuyển vế.

- Tìm điều kiện xác định.

- Qui đồng khử mẫu.

- Giải phương trình bằng cách chuyển vế.

- Tìm điều kiện xác định.

- Qui đồng khử mẫu.

- Giải phương trình bằng cách chuyển vế.

Lời giải:

Điều kiện xác định: $x - 2 \neq 0$ , tức là $x \neq 2$ .

Quy đồng mẫu thức:

$\frac{1}{x - 2} + 3 = \frac{x - 3}{2 - x}$

$\Leftrightarrow \frac{1}{x - 2} + \frac{3 (x - 2)}{x - 2} = - \frac{x - 3}{x - 2}$

Khử mẫu thức, ta được phương trình:

$1 + 3 (x - 2) = - (x - 3)$

Giải phương trình nhận được:

$1 + 3 x - 6 = - x + 3$

$\Leftrightarrow 3 x + x = 3 + 6 - 1$

$\Leftrightarrow 4 x = 8$

$\Leftrightarrow x = 2$

Kiểm tra kết quả: $x = 2$ không thỏa mãn ĐKXĐ.

Kết luận: Vậy phương trình vô nghiệm.

Điều kiện xác định: $x + 3 \neq 0$ , tức là $x \neq - 3$

Quy đồng mẫu thức:

$\frac{2 x .7 . (x + 3)}{7. (x + 3)} - \frac{2.7. x^{2}}{7. (x + 3)}$ $= \frac{7.4. x}{7. (x + 3)} + \frac{2 (x + 3)}{7 (x + 3)}$

Khử mẫu ta được:

$14 x (x + 3) - 14 x^{2} = 28 x + 2 (x + 3)$

Giải phương trình nhận được:

$14 x^{2} + 42 x - 14 x^{2} = 28 x + 2 x + 6$

⇔ $42 x - 30 x = 6$

⇔ $12 x = 6$

⇔ $x = \frac{6}{12}$

⇔ $x = \frac{1}{2}$

Kiểm tra: $x = \frac{1}{2}$ thỏa mãn ĐKXĐ.

Kết luận: Vậy phương trình có nghiệm $x = \frac{1}{2}$ .

Điều kiện xác định: $x - 1 \neq 0; x + 1 \neq 0$ , tức là $x \neq \pm 1$

Quy đồng mẫu thức:

$\frac{(x + 1) . (x + 1)}{x^{2} - 1} - \frac{(x - 1) . (x - 1)}{x^{2} - 1}$ $= \frac{4}{x^{2} - 1}$

$\Leftrightarrow \frac{{(x + 1)}^{2} - {(x - 1)}^{2}}{x^{2} - 1}$ $= \frac{4}{x^{2} - 1}$

Khử mẫu ta được: ${(x + 1)}^{2} - {(x - 1)}^{2} = 4$

Giải phương trình:

$x^{2} + 2 x + 1 - (x^{2} - 2 x + 1) = 4$

$\Leftrightarrow x^{2} + 2 x + 1 - x^{2} + 2 x - 1 = 4$

$\Leftrightarrow 4 x = 4$

$\Leftrightarrow x = 4 : 4$

$\Leftrightarrow x = 1$

Kiểm tra $x = 1$ không thỏa mãn ĐKXĐ.

Kết luận: Vậy phương trình vô nghiệm.

Điều kiện xác định: $x + 7 \neq 0; 2 x - 3 \neq 0$ , tức là $x \neq - 7$ và $x \neq \frac{3}{2}$

Quy đồng mẫu thức ta được:

$\frac{(3 x - 2) (2 x - 3)}{(x + 7) (2 x - 3)}$ $= \frac{(6 x + 1) (x + 7)}{(x + 7) (2 x - 3)}$

Khử mẫu ta được: $(3 x - 2) (2 x - 3) = (6 x + 1) (x + 7)$

Giải phương trình:

$6 x^{2} - 9 x - 4 x + 6$ $= 6 x^{2} + 42 x + x + 7$

$\Leftrightarrow 6 x^{2} - 13 x + 6 = 6 x^{2} + 43 x + 7$

$\Leftrightarrow 6 x^{2} - 13 x - 6 x^{2} - 43 x = 7 - 6$

$\Leftrightarrow - 56 x = 1$

$\Leftrightarrow x = \frac{- 1}{56}$

Kiểm tra kết quả: $x = \frac{- 1}{56}$ thỏa mãn ĐKXĐ.

Kết luận: Vậy phương trình có nghiệm $x = \frac{- 1}{56}$ .

Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 20: Giải các phương trình:

\frac{1}{x - 1} - \frac{3 x^{2}}{x^{3} - 1} = \frac{2 x}{x^{2} + x + 1}

\frac{3}{(x - 1) (x - 2)}

\frac{2}{(x - 3) (x - 1)}

\frac{1}{(x - 2) (x - 3)}

1 + \frac{1}{x + 2} = \frac{12}{8 + x^{3}}

\frac{13}{(x - 3) (2 x + 7)} + \frac{1}{2 x + 7}

= \frac{6}{(x - 3) (x + 3)}

Phương pháp giải:

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: $A (x) . B (x) = 0$

$\Leftrightarrow A (x) = 0$ hoặc $B (x) = 0$

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: $A (x) . B (x) = 0$

$\Leftrightarrow A (x) = 0$ hoặc $B (x) = 0$

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: $A (x) . B (x) = 0$

$\Leftrightarrow A (x) = 0$ hoặc $B (x) = 0$

Lời giải:

Điều kiện xác định: $x^{3} - 1 \neq 0$ tức là $x \neq 1$

Quy đồng mẫu thức:

$\frac{1}{x - 1} - \frac{3 x^{2}}{x^{3} - 1} = \frac{2 x}{x^{2} + x + 1}$

$\Leftrightarrow \frac{x^{2} + x + 1 - 3 x^{2}}{x^{3} - 1} = \frac{2 x (x - 1)}{x^{3} - 1}$

Khử mẫu thức, ta được phương trình

$x^{2} + x + 1 - 3 x^{2} = 2 x (x - 1)$

Giải phương trình nhận được:

$- 2 x^{2} + x + 1 = 2 x^{2} - 2 x$

$\Leftrightarrow 0 = 2 x^{2} - 2 x + 2 x^{2} - x - 1$

$\Leftrightarrow 0 = 4 x^{2} - 3 x - 1$

$\Leftrightarrow 4 x^{2} - 3 x - 1 = 0$

$\Leftrightarrow 4 x^{2} - 4 x + x - 1 = 0$

$\Leftrightarrow 4 x (x - 1) + (x - 1) = 0$

$\Leftrightarrow (x - 1) (4 x + 1) = 0$

$\Leftrightarrow [\begin{matrix} x - 1 = 0 \\ 4 x + 1 = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 1 \\ x = - \frac{1}{4} \end{matrix}$

Kiểm tra kết quả: Giá trị $x = 1$ bị loại do không thỏa mãn điều kiện xác định, giá trị $x = - \frac{1}{4}$ thỏa mãn điều kiện xác định.

Kết luận: Vậy phương trình có nghiệm duy nhất $x = - \frac{1}{4}$

$\frac{3}{(x - 1) (x - 2)} + \frac{2}{(x - 3) (x - 1)}$ $= \frac{1}{(x - 2) (x - 3)}$

Điều kiện xác định: $x - 1 \neq 0; x - 2 \neq 0; x - 3 \neq 0$ , tức là $x \neq 1, 2, 3$ .

Quy đồng mẫu thức:

$\frac{3}{(x - 1) (x - 2)} + \frac{2}{(x - 3) (x - 1)}$ $= \frac{1}{(x - 2) (x - 3)}$

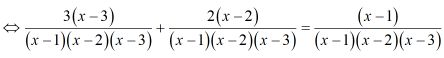
Khử mẫu thức, ta được phương trình:

$3 (x - 3) + 2 (x - 2) = x - 1$

Giải phương trình nhận được:

$3 x - 9 + 2 x - 4 = x - 1$

$\Leftrightarrow 4 x = 12$

$\Leftrightarrow x = 3$

Kiểm tra kết quả: Giá trị $x = 3$ không thỏa mãn ĐKXĐ.

Vậy phương trình vô nghiệm.

Điều kiện xác định: $8 + x^{3} \neq 0$ , tức là $x \neq - 2$ .

Quy đồng mẫu thức:

$1 + \frac{1}{x + 2} = \frac{12}{8 + x^{3}}$

$\Leftrightarrow \frac{8 + x^{3}}{8 + x^{3}} + \frac{x^{2} - 2 x + 4}{8 + x^{3}} = \frac{12}{8 + x^{3}}$

Khử mẫu thức, ta được phương trình:

$x^{3} + 8 + x^{2} - 2 x + 4 = 12$

Giải phương trình nhận được:

$x^{3} + x^{2} - 2 x = 12 - 8 - 4$

$\Leftrightarrow x^{3} + x^{2} - 2 x = 0$

$\Leftrightarrow x (x^{2} + x - 2) = 0$

$\Leftrightarrow x [x^{2} + 2 x - x - 2] = 0$

⇔ $x [x (x + 2) - (x + 2)] = 0$

⇔ $x (x + 2) (x - 1) = 0$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x + 2 = 0 \\ x - 1 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 2 \\ x = 1 \end{array}$

Kiểm tra kết quả: Giá trị $x = 0; x = 1$ thỏa mãn ĐKXĐ; giá trị $x = - 2$ không thỏa mãn ĐKXĐ.

Kết luận: Vậy phương trình có tập nghiệm là $S = {0; 1}$ .

Điều kiện xác định: $x - 3 \neq 0; x + 3 \neq 0$ và $2 x + 7 \neq 0$ , tức là $x \neq \pm 3, x \neq - 3, 5$

Quy đồng mẫu thức:

$\frac{13}{(x - 3) (2 x + 7)} + \frac{1}{2 x + 7}$ $= \frac{6}{(x - 3) (x + 3)}$

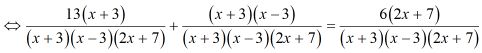
Khử mẫu thức, ta được phương trình:

$13 (x + 3) + (x - 3) (x + 3)$ $= 6 (2 x + 7)$

Giải phương trình nhận được:

$13 x + 39 + x^{2} - 9 = 12 x + 42$

$\Leftrightarrow x^{2} + x - 12 = 0$

$\Leftrightarrow x^{2} + 4 x - 3 x - 12 = 0$

$\Leftrightarrow x (x + 4) - 3 (x + 4) = 0$

$\Leftrightarrow (x - 3) (x + 4) = 0$

$\Leftrightarrow [\begin{array}{l} x = 3 (không thỏa mãn) \\ x = - 4 (thỏa mãn) \end{array}$

Kiểm tra kết quả: Giá trị $x = 3$ bị loại vì không thỏa mãn ĐKXĐ, giá trị $x = - 4$ thỏa mãn ĐKXĐ.

Kết luận: Vậy phương trình có nghiệm duy nhất $x = - 4$ .

Vở bài tập Toán 8 trang 17, 18, 19, 20, 21, 22, 23 Bài 21: Tìm các giá trị của

a

sao cho mỗi biểu thức sau có giá trị bằng

2

\frac{3 a - 1}{3 a + 1} + \frac{a - 3}{a + 3}

\frac{10}{3} - \frac{3 a - 1}{4 a + 12} - \frac{7 a + 2}{6 a + 18}

Phương pháp giải:

Cho giá trị biểu thức bằng 2 bài toán trở thành bài toán giải phương trình chứa ẩn ở mẫu ( với ẩn a)

B1: Đặt ĐKXĐ của phương trình.

B2: Quy đồng khử mẫu

B3: Sử dụng quy tắc chuyển vế để tìm a.

B4: Kết luận (Kiểm tra giá trị của a tìm được có thỏa mãn với ĐKXĐ không)

Cho giá trị biểu thức bằng 2 bài toán trở thành bài toán giải phương trình chứa ẩn ở mẫu ( với ẩn a)

B1: Đặt ĐKXĐ của phương trình.

B2: Quy đồng khử mẫu

B3: Sử dụng quy tắc chuyển vế để tìm a.

B4: Kết luận (Kiểm tra giá trị của a tìm được có thỏa mãn với ĐKXĐ không)

Lời giải:

Bài toán quy về việc giải phương trình ẩn $a$ :

$\frac{3 a - 1}{3 a + 1} + \frac{a - 3}{a + 3} = 2$ ;

Điều kiện xác định: $3 a + 1 \neq 0; a + 3 \neq 0$ , tức là $a \neq - \frac{1}{3}, a \neq - 3$ .

Quy đồng mẫu thức hai vế:

$\frac{(3 a - 1) (a + 3)}{(3 a + 1) (a + 3)} + \frac{(a - 3) (3 a + 1)}{(3 a + 1) (a + 3)}$ $= \frac{2 (3 a + 1) (a + 3)}{(3 a + 1) (a + 3)}$

Khử mẫu thức, ta được phương trình:

$(3 a - 1) (a + 3) + (a - 3) (3 a + 1)$ $= 2 (3 a + 1) (a + 3)$

Giải phương trình nhận được:

⇔ $3 a^{2} + 9 a - a - 3 + 3 a^{2} - 9 a + a - 3$ $= 6 a^{2} + 18 a + 2 a + 6$

$\Leftrightarrow - 20 a = 12$

⇔ $a = 12 : (- 20)$

⇔ $a = - \frac{3}{5}$

Kiểm tra kết quả: Giá trị $a = - \frac{3}{5}$ thỏa mãn ĐKXĐ.

Trả lời: Vậy $a = - \frac{3}{5}$ thì biểu thức $\frac{3 a - 1}{3 a + 1} + \frac{a - 3}{a + 3}$ có giá trị bằng $2$ .

Bài toán quy về việc giải phương trình ẩn $a$ :

$\frac{10}{3} - \frac{3 a - 1}{4 a + 12} - \frac{7 a + 2}{6 a + 18} = 2$

Điều kiện xác định: $4 a + 12 \neq 0; 6 a + 18 \neq 0$ , tức là $a \neq - 3.$

Quy đồng mẫu thức hai vế:

$\frac{4.10 (a + 3)}{12 (a + 3)} - \frac{3 (3 a - 1)}{12 (a + 3)}$ $- \frac{2 (7 a + 2)}{12 (a + 3)} = \frac{2.12 (a + 3)}{12 (a + 3)}$

Khử mẫu thức, ta được phương trình:

$40 (a + 3) - 3 (3 a - 1) - 2 (7 a + 2)$ $= 24 (a + 3)$

Giải phương trình nhận được:

$40 a + 120 - 9 a + 3 - 14 a - 4$ $= 24 a + 72$

⇔ $- 7 a = - 47$

⇔ $a = \frac{47}{7}$

Kiểm tra kết quả: Giá trị $a = \frac{47}{7}$ thỏa mãn ĐKXĐ.

Trả lời: Biểu thức đã cho

\frac{10}{3} - \frac{3 a - 1}{4 a + 12} - \frac{7 a + 2}{6 a + 18}

có giá trị bằng

2

khi

a = \frac{47}{7}

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

227

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

286

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

236