Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Bảng phân bố tần số và tần suất (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Bảng phân bố tần số và tần suất (HAY NHẤT 2024)
A. Lí thuyết
1. Số liệu thống kê
Số liệu thống kê được định nghĩa là các số liệu thu thập được khi điều tra về một dấu hiệu. Khi thực hiện việc điều tra thống kê (theo mục đích đã định trước) thì ta cần phải xác định được tập hợp các đơn vị điều tra, dấu hiệu điều tra cũng như thu thập số liệu.
2. Tần số, tần suất
+ Tần số: Tần số của một giá trị x là số lần xuất hiện của giá trị x trong bảng số liệu thống kê.
+ Tần suất: Tần suất được định nghĩa chính là tỉ số f giữa tần số và kích thước của tập hợp các đơn vị điều tra.
+ Giả sử dãy n số liệu thống kê đã cho có k giá trị khác nhau là với . Khi đó ta gọi số lần xuất hiện giá trị trong dãy số n số liệu thống kê đã cho là tần số của giá trị đó, kí hiệu , từ đó ta có: . Tỉ số được gọi là tần suất của giá trị với , người ta thường viết tần suất dưới dạng tỉ số phần trăm, từ đó ta có:
- Tần số, tần suất của lớp:
Giả sử n số liệu thống kê đã cho được phân vào k lớp không giao nhau ().
Ta định nghĩa:
+ Tần số của lớp thứ i là số các số liệu thống kê thuộc vào lớp đó. Ta có:
+ Tần suất của lớp thứ i là tỉ số . Trong các bảng phân bố tần suất ghép lớp, tần suất được tính ở dạng tỉ số phần trăm. Ta có:
3. Các bước để lập bảng phân bố tần số và tần suất
Bước 1: Xác định các giá trị trong dãy n số liệu thống kê đã cho () và xác định các tần số của các giá trị này.
Bước 2: Tính tần suất của giá trị với .
Bước 3: Tập hợp các kết quả tìm được ở bước trên (các giá trị , tần số , tần suất ) thành một bảng. Trong bảng, các giá trị thường được xếp theo thứ tự tăng dần hoặc giảm dần.
4. Các bước đế lập bảng phân bố tần số và tần suất ghép lớp
+ Phân lớp.
+ Xác định tần số, tần suất của các lớp.
+ Thành lập bảng.
- Ý nghĩa: Các bảng phân bố tần số, tần suất ghép lớp phản ánh tình hình phân bố của các số liệu thống kê.
B. Các dạng bài
Dạng 1: Lập bảng phân bố tần số và tần suất
Phương pháp giải:
Bước 1: Xác định các giá trị trong dãy n số liệu thống kê đã cho () và xác định các tần số của các giá trị này.
Bước 2: Tính tần suất của giá trị với .
Bước 3: Tập hợp các kết quả tìm được ở bước trên (các giá trị , tần số , tần suất ) thành một bảng. Trong bảng, các giá trị thường được xếp theo thứ tự tăng dần hoặc giảm dần.
Ví dụ minh họa:
Bài 1: Cho các số liệu thống kê ghi trong bảng sau là tuổi thọ của 30 bóng đèn điện được thắp thử (đơn vị: giờ). Hãy lập bảng phân bố tần số và bảng phân bố tần suất
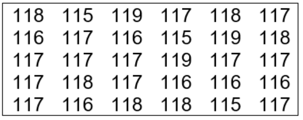
Lời giải:
Trong n = 30 số liệu đã cho có 5 giá trị khác nhau: , , ,,
Tần số của các giá trị này lần lượt là: , , , ,
Từ đó, ta có bảng phân bố tần số như sau:
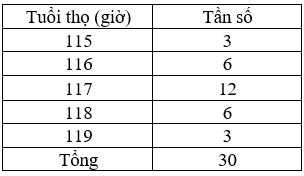
Dựa vào bảng phân bố tần số, ta tính được tần suất:
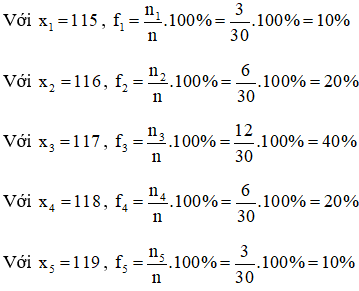
Từ đó, ta có bảng phân bố tần suất:
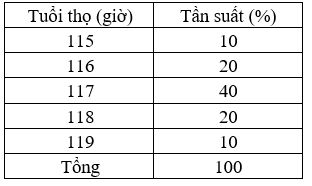
Bài 2: Cho các số liệu thống kê trong bảng sau là thời gian hoàn thành một sản phẩm ở một nhóm công nhân (đơn vị: phút). Hãy lập bảng phân bố tần số và tần suất.
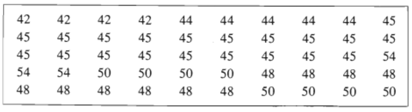
Lời giải:
Trong n = 50 số liệu đã cho có 6 giá trị khác nhau: , , , , ,
Tần số và tần suất của các giá trị này lần lượt là:
Với , tần số và tần suất
Với , tần số và tần suất
Với , tần số và tần suất
Với , tần số và tần suất
Với , tần số và tần suất
Với , tần số và tần suất
Từ đó, ta có bảng phân bố tần số và tần suất:
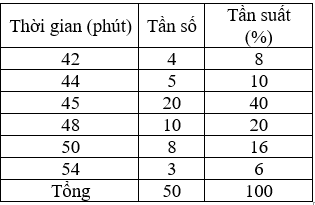
Dạng 2: Lập bảng phân bố tần số và tần suất ghép lớp.
Phương pháp giải:
+ Phân lớp.
+ Xác định tần số, tần suất của các lớp.
+ Thành lập bảng.
Ví dụ minh họa:
Bài 1: Cho bảng số liệu sau là giá cổ phiếu tháng 4 (nghìn đồng) của ngân hàng A lúc mở cửa. Hãy lập bảng phân phối tần số và tần suất ghép lớp với các lớp như sau: [44; 47), [47; 49), [49; 56).
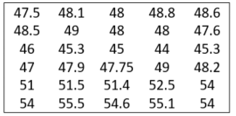
Lời giải:
Trong n = 30 số liệu đã cho, ta có:
Tần số của lớp thứ nhất [44; 47) là và tần suất là
Tần số của lớp thứ hai [47; 49) là và tần suất là
Tần số của lớp thứ ba [49; 56) là và tần suất là
Từ đó, ta có bảng phân bố tần số và tần suất ghép lớp:
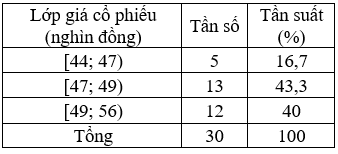
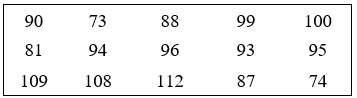
Bài 2: Cho các số liệu thống kê trong bảng sau là khối lượng (đơn vị: g) của 15 củ khoai tây được trồng ở mảnh vườn D. Hãy lập bảng phân bố tần số và tần suất ghép lớp với các lớp như sau: [70; 90), [90; 120).
Lời giải:
Trong n = 15 số liệu đã cho, ta có:
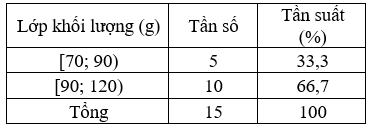
Tần số của lớp thứ nhất [70; 90) là và tần suất là
Tần số của lớp thứ hai [90; 120) là và tần suất là
Từ đó, ta có bảng phân bố tần số và tần suất ghép lớp:
C. Bài tập vận dụng
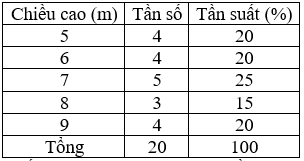
Bài 1: Cho các số liệu thống kê trong bảng sau là chiều cao (đơn vị: m) của 20 cây cao su. Hãy lập bảng phân bố tần số và tần suất.
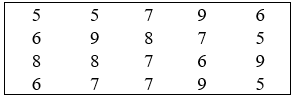
Đáp án:
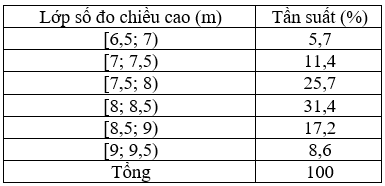
Bài 2: Cho các số liệu thống kê trong bảng sau là chiều cao (đơn vị: m) của 35 cây bạch đàn. Hãy lập bảng phân bố tần suất ghép lớp với các lớp : [6,5; 7), [7; 7,5), [7,5; 8), [8; 8,5), [8,5; 9), [9; 9,5).

Đáp án:
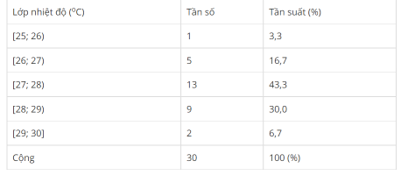
Bài 3: Cho các số liệu thống kê ghi trong bảng sau là nhiệt độ trung bình () của tháng 5 ở địa phương A từ 1961 đến 1990. Lập bảng phân bố tần số và tần suất ghép lớp, với các lớp sau [25; 26), [26; 27), [27; 28), [28; 29), [29; 30)

Đáp án:
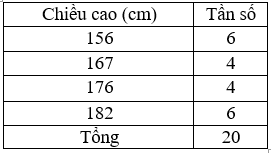
Bài 4: Cho các số liệu thống kê ghi trong bảng sau là chiều cao của 40 học sinh lớp 11 ở trường Trung học phổ thông M (đơn vị: cm). Hãy lập bảng phân bố tần số.

Đáp án:
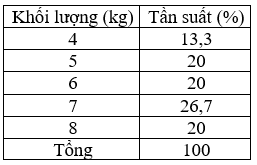
Bài 5: Cho các số liệu thống kê ghi trong bảng sau là khối lượng của 15 con heo ở trang trại X (đơn vị: kg). Hãy lập bảng phân bố tần suất.
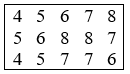
Đáp án:
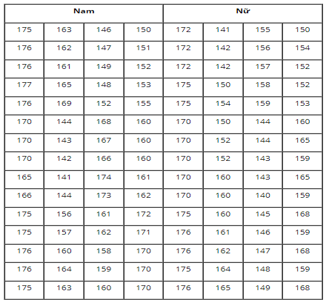
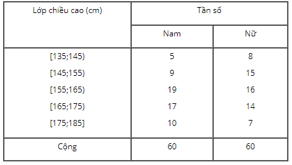
Bài 6: Cho các số liệu thống kê ghi trong bảng sau là chiều cao của 120 học sinh lớp 11 ở trường Trung học phổ thông M (đơn vị: cm). Hãy lập bảng phân bố tần số ghép lớp (đồng thời theo chiều cao của nam và của nữ) với các lớp [135; 145), [145; 155), [155; 165), [165; 175), [175; 185).
Đáp án:
Bài 7: Cho bảng phân bố tần số ghép lớp tỷ lệ % các trường mầm non đạt chuẩn Quốc gia trong năm học 2013 – 2014 của 63 tỉnh, thành phố. Tần suất của lớp thứ ba (làm tròn đến hàng phần trăm) là bao nhiêu ?
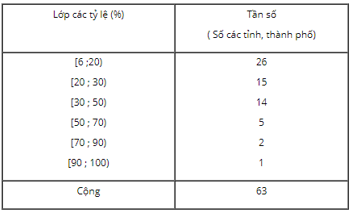
Đáp án: 22%
Bài 8: Cho bảng phân bố tần số và tần suất: Điểm kiểm tra 15 phút môn toán của một lớp học. Vậy (*) nhận giá trị là bao nhiêu ? (làm tròn đến chữ số thập phân thứ 2)
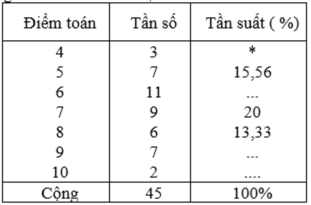
Đáp án: 6,67
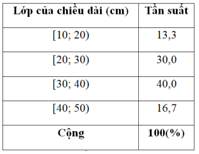
Bài 9: Cho bảng phân bố tần số ghép lớp: Chiều dài của 60 lá dương xỉ trưởng thành. Hãy lập bảng phân bố tần suất ghép lớp.
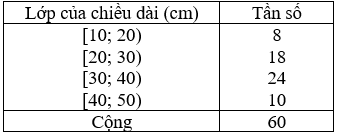
Đáp án:
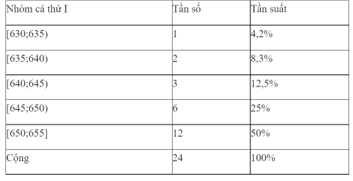
Bài 10: Cho các số liệu thống kê được ghi trong bảng sau:

Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là [630; 635), [635; 640), [640; 645), [645; 650), [650; 655)
Đáp án:
D. Bài tập tự luyện
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Biểu đồ lớp 10 và cách giải bài tập
Số trung bình cộng. Số trung vị. Mốt và cách giải bài tập
Phương sai và độ lệch chuẩn và cách giải bài tập
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.