Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Giá trị lượng giác của một góc bất kì từ 0 đến 180 (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Phương pháp giải Giá trị lượng giác của một góc bất kì từ 0 đến 180 (HAY NHẤT 2024)

A. Lí thuyết

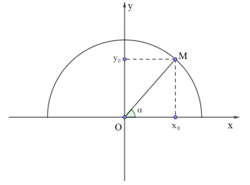
- Định nghĩa: Cho góc $\alpha$ ($0^o\le \alpha \le {180}^o$) bất kì, xác định một điểm $M(x_0;y_0)$ trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Khi đó ta có: $\sin \alpha =y_0$; $\cos \alpha =x_0$; $\tan \alpha =\frac{y_0}{x_0}\left(x_0\ne 0\right)$; $\cot \alpha =\frac{x_0}{y_0}\left(y_0\ne 0\right)$. ( sin, cos, tan, cot là các giá trị lượng giác của góc $\alpha$)

- Tính chất:

Hai góc bù nhau là hai góc có tổng bằng ${180}^o$. Cho góc $\alpha$ ta có:

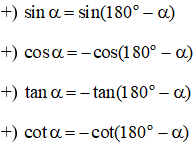
Hai góc phụ nhau là hai học có tổng bằng ${90}^o$. Cho góc $\alpha$ ta có:

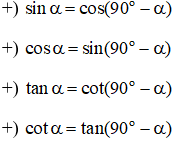
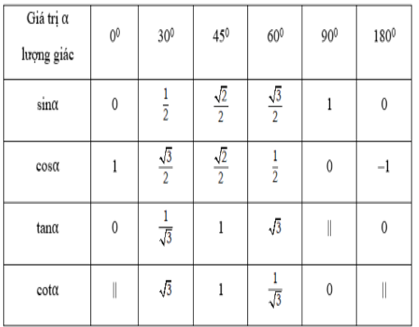
- Bảng giá trị lượng giác của các góc đặc biệt:

- Định nghĩa góc giữa hai vectơ: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}$. Từ điểm O bất kì vẽ $\overrightarrow{OA}=\overrightarrow{a}$, $\overrightarrow{OB}=\overrightarrow{b}$, khi đó góc $\widehat{AOB}$ ($0^o\le \widehat{AOB}\le {180}^o$) là góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$. Kí hiệu: $\left(\overrightarrow{a},\overrightarrow{b}\right)$.

- Các hệ thức cơ bản liên hệ giữa các giá trị lượng giác :

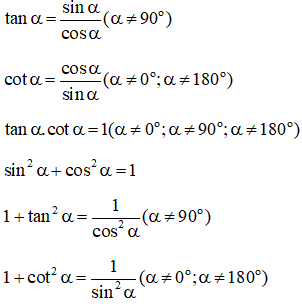
- Chú ý:

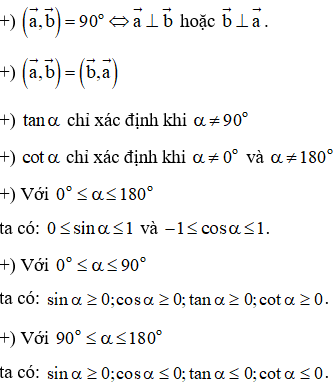
B. Các dạng bài

Dạng 1: Góc và dấu của các giá trị lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.

Ví dụ minh họa:

Bài 1: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {90}^o$. Xác định dấu của các giá trị lượng giác sau: $\sin (\alpha +{90}^o)$; $\cos \alpha$; $\tan (\alpha +{90}^o)$.

Lời giải:

Ta có:

 $0^o\le \alpha \le {90}^o\Rightarrow {90}^o\le \alpha +{90}^o\le {180}^o$

Khi $0^o\le \alpha \le {90}^o$, ta có: $\cos \alpha \ge 0\Rightarrow \cos \alpha$  mang dấu dương hoặc bằng 0.

Khi ${90}^o\le \alpha +{90}^o\le {180}^o$ ta có:$\sin (\alpha +{90}^o)\ge 0$ ; $\tan (\alpha +{90}^o)\le 0$

$\sin (\alpha +{90}^o)$  mang dấu dương hoặc bằng 0 và $\tan (\alpha +{90}^o)$ mang dấu âm hoặc bằng 0.

Bài 2: Trên đường tròn đơn vị cho điểm $M\left(\frac{\sqrt{3}}{2};\frac{1}{2}\right)$. Xác định góc $\widehat{xOM}$.

Lời giải:

Điểm  $M\left(\frac{\sqrt{3}}{2};\frac{1}{2}\right)\Rightarrow \sin \widehat{\text{x}OM}=\frac{1}{2}$; $\cos \widehat{xOM}=\frac{\sqrt{3}}{2}$

Dựa vào các giá trị lượng giác đặc biệt ta suy ra $\widehat{xOM}={30}^o$.

Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.

Ví dụ minh họa:

Bài 1: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {180}^o$ biết $\cos \alpha =\frac{-2}{3}$, hãy tính các giá trị lượng giác $\sin \alpha ,\cot \alpha ,\tan \alpha$.

Lời giải:

Áp dụng các hệ thức cơ bản liên hệ giữa  các giá trị lượng giác ta có:

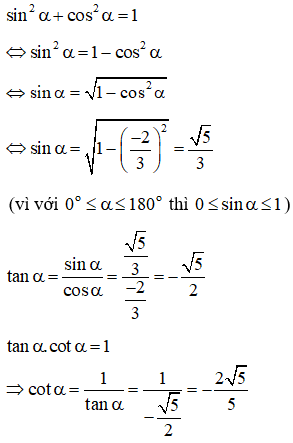
Bài 2: Cho góc  thỏa mãn $0^o\le \alpha \le {90}^o$ , biết $\tan \alpha =2$. Tính các giá trị lượng giác $\cot \alpha ,\cos \alpha ,\sin \alpha$.

Lời giải:

Áp dụng các hệ thức cơ bản liên hệ giữa các giá trị lượng giác ta có:

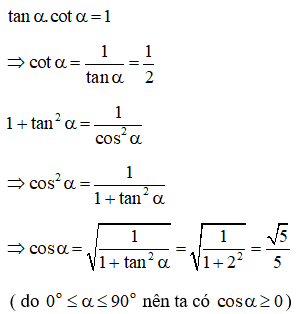
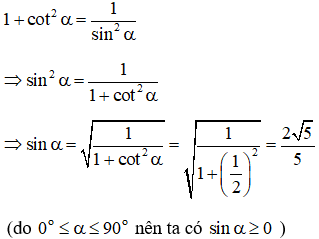
Dạng 3: Chứng minh, rút gọn một biểu thức lượng giác.

Phương pháp giải:

Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).

Ví dụ minh họa:

Bài 1: Chứng minh đẳng thức:

$a^2\sin {90}^o+b^2\cos {90}^o+c^2\cos {180}^o=(a-c)(a+c)$

Lời giải:

Theo bảng các giá trị lượng giác đặc biệt ta có:

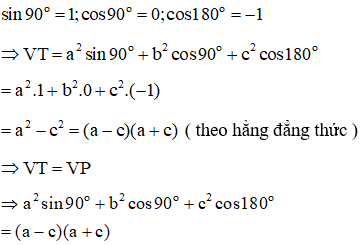
(điều cần phải chứng minh)

C. Bài tập vận dụng 

Bài 1: Cho góc $\alpha ={54}^o$. Nhận định nào sau đây là đúng ?

A. $\sin \alpha <0$

B. $\tan \alpha <0$

C. $\cos \alpha >0$

D. $\cot \alpha <0$

Đáp án: C

Bài 2: Cho biết $\sin \alpha >0;\cos \alpha <0$. Góc $\alpha$ có thể là góc nào sau đây:

A. $\alpha ={50}^o$

B. $\alpha ={45}^o$

C. $\alpha =0^o$

D. $\alpha ={112}^o$

Đáp án: D

Bài 3: Cho điểm M (1;0) trên đường tròn đơn vị. Hãy xác định số đo của góc $\widehat{xOM}$.

Đáp án: $\widehat{xOM}=0^o$

Bài 4: Cho góc $\alpha$ thỏa mãn ${10}^o\le \alpha \le {80}^o$. Hãy xác định dấu của các giá trị lượng giác $\sin (\alpha +{90}^o)$,$\cos \alpha$ .

Đáp án: $\sin (\alpha +{90}^o)$ mang dấu dương, $\cos \alpha$ mang dấu dương

Bài 5: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {180}^o$ biết $\cos \alpha =\frac{1}{2}$, hãy tính các giá trị lượng giác $\sin \alpha ,\cot \alpha ,\tan \alpha$.

Đáp án:

$\sin \alpha =\frac{\sqrt{3}}{2};\tan \alpha =\sqrt{3};\cot \alpha =\frac{1}{\sqrt{3}}$

Bài 6: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {180}^o$ biết $\cot \alpha =3$, hãy tính các giá trị lượng giác $\sin \alpha ,\cos \alpha ,\tan \alpha$.

Đáp án:

$\sin \alpha =\frac{\sqrt{10}}{10};\tan \alpha =\frac{1}{3};\cos \alpha =\frac{3\sqrt{10}}{10}$

Bài 7: Cho góc $\alpha$ thỏa mãn $0^o\le \alpha \le {90}^o$, biết $\cos \alpha -\sin \alpha =\frac{1}{2}$. Tính các giá trị lượng giác $\tan \alpha ,\cot \alpha$.

Đáp án: $\tan \alpha =\frac{4-\sqrt{7}}{3};\cot \alpha =\frac{4+\sqrt{7}}{3}$

Bài 8: Chứng minh đẳng thức: $\frac{1+\cot \alpha }{1-\cot \alpha }=\frac{\tan \alpha +1}{\tan \alpha -1}$.

Đáp án:

$VT=\frac{1+\cot \alpha }{1-\cot \alpha }=\frac{1+\frac{1}{\tan \alpha }}{1-\frac{1}{\tan \alpha }}=\frac{\tan \alpha +1}{\tan \alpha -1}=VP$

Bài 9: Chứng minh đẳng thức: $\frac{\sin \alpha +\cos \alpha }{{\cos }^3\alpha }={\tan }^3\alpha +{\tan }^2\alpha +\tan \alpha +1$.

Đáp án:

$$\begin{gathered} VT=\frac{\sin \alpha +\cos \alpha }{{\cos }^3\alpha }=\frac{\sin \alpha }{\cos \alpha }.\frac{1}{{\cos }^2\alpha }+\frac{1}{{\cos }^2\alpha } \\ ={\tan }^3\alpha +{\tan }^2\alpha +\tan \alpha +1=VP \end{gathered}$$

Bài 10: Rút gọn và tính giá trị biểu thức: $B={\sin }^2{15}^o+{\sin }^2{3}^o+{\sin }^2{75}^o+{\sin }^2{87}^o$

Đáp án: B = 2

D. Bài tập tự luyện 

Câu 1. Rút gọn biểu thức sau $A=\frac{{\cot }^{2}x-{\cos }^{2}x}{{\cot }^{2}x}+\frac{\sin x.\cos x}{\cot x}$.

A. A=1.

B. A=2.

C. A=3.

D. A=4

Câu 2. Cho biết $\tan \alpha =\frac{1}{2}$. Tính $\cot \alpha$.

A. $\cot \alpha =2$.

B. $\cot \alpha =\sqrt{2}$.

C. $\cot \alpha =\frac{1}{4}$.

D. $\cot \alpha =\frac{1}{2}$.

Câu 3. Trong các mệnh đề sau, mệnh đề nào sai?

A. ${\left(\sin x\cos x\right)}^2=12\sin x\cos x$

B. ${\sin }^{4}x+{\cos }^{4}x=12{\sin }^{2}x{\cos }^{2}x$

C. ${\left(\sin x+\cos x\right)}^2=1+2\sin x\cos x$

D.  ${\sin }^{6}x+{\cos }^{6}x=1{\sin }^{2}x{\cos }^{2}x$

Câu 4. Khẳng định nào sau đây là sai?

A. ${\sin }^2\alpha +{\cos }^2\alpha =1$

B. $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }\left(\sin \alpha \ne 0\right)$

C. $\tan \alpha .\cot \alpha =-1\left(\sin \alpha .\cos \alpha \ne 0\right)$

D. $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }\left(\cos \alpha \ne 0\right)$

Câu 5. Biểu thức $f\left(x\right)=3\left({\sin }^{4}x+{\cos }^{4}x\right)-2\left({\sin }^{6}x+{\cos }^{6}x\right)$ có giá trị bằng:

A. 1.

B. 2.

C. -3.

D. 0.

Câu 6. Biểu thức: $f\left(x\right)={\cos }^{4}x+{\cos }^{2}x{\sin }^{2}x+{\sin }^{2}x$ có giá trị bằng

A. 1.

B. 2.

C. -2.

D. -1.

Câu 7. Biểu thức ${\tan }^{2}x{\sin }^{2}x-{\tan }^{2}x+{\sin }^{2}x$ có giá trị bằng

A. -1.

B. 0 .

C. 2.

D. 1.

Câu 8. Giá trị của $A=\tan 5^{°}.\tan {10}^{°}.\tan {15}^{°}\mathrm{...}\tan {80}^{°}.\tan {85}^{°}$ là

A. 2.

B. 1.

C. 0.

D. -1.

Câu 9. Chọn mệnh đề đúng?

A. ${\sin }^{4}x-{\cos }^{4}x=1-2{\cos }^{2}x$.

B. ${\sin }^{4}x-{\cos }^{4}x=1-2{\sin }^{2}x{\cos }^{2}x$

C. ${\sin }^{4}x-{\cos }^{4}x=1-2{\sin }^{2}x$

D. ${\sin }^{4}x-{\cos }^{4}x=2{\cos }^{2}x-1$

Câu 10. Rút gọn biểu thức $P=\frac{1-si{n}^{2}x}{2\sin x.\cos x}$ ta được

A. $P=\frac{1}{2}\tan x$ .

B. $P=\frac{1}{2}\cot x$ .

C. $P=2\cot x$ .

D. $P=2\tan x$.

Câu 11. Giá trị của $B={\cos }^2{73}^{°}+{\cos }^2{87}^{°}+{\cos }^2{3}^{°}+{\cos }^2{17}^{°}$ là

A. $\sqrt{2}$.

B. 2.

C. -2.

D. 1.

Câu 12. Cho $cot\alpha =\frac{1}{3}$. Giá trị của biểu thức $A=\frac{3\sin \alpha +4\cos \alpha }{2\sin \alpha -5\cos \alpha }$ là:

A. $-\frac{15}{13}$.

B. $-13$.

C. $\frac{15}{13}$.

D. $13$.

Câu 13. Giá trị của $\tan {30}^{°}+\cot {30}^{°}$ bằng bao nhiêu?

A. $\frac{4}{\sqrt{3}}$

B. $\frac{1+\sqrt{3}}{3}$

C. $\frac{2}{\sqrt{3}}$

D. 2.

Câu 14. Trong các đẳng thức sau đây, đẳng thức nào sai?

A. $\sin 0^{°}+\cos 0^{°}=1$.

B. $\sin {90}^{°}+\cos {90}^{°}=1$.

C. $\sin {180}^{°}+\cos {180}^{°}=-1$.

D. $\sin {60}^{°}+\cos {60}^{°}=1$.

Câu 15. Trong các khẳng định sau, khẳng định nào sai?

A. $\cos {60}^{°}=\sin {30}^{°}$.

B. $\cos {60}^{°}=\sin {120}^{°}$.

C. $\cos {30}^{°}=\sin {120}^{°}$.

D. $\sin {60}^{°}=-\cos {120}^{°}$.

Câu 16. Giá trị của $\tan {45}^{°}+\cot {135}^{°}$ bằng bao nhiêu?

A. 2.

B. 0.

C. $\sqrt{3}$.

D. 1.

Câu 17. Giá trị của $\cos {30}^{°}+\sin {60}^{°}$ bằng bao nhiêu?

A. $\frac{\sqrt{3}}{3}$.

B. $\frac{\sqrt{3}}{2}$.

C. $\sqrt{3}$.

D. 1.

Câu 18. Giá trị của $E=\sin {36}^{°}\cos 6^{°}\sin {126}^{°}\cos {84}^{°}$ là

A. $\frac{1}{2}$ .

B. $\frac{\sqrt{3}}{2}$.

C. 1.

D. -1.

Câu 19. Đẳng thức nào sau đây sai?

A. $\sin {45}^{°}+\sin {45}^{°}=\sqrt{2}$.

B. $\sin {30}^{°}+\cos {60}^{°}=1$.

C. $\sin {60}^{°}+\cos {150}^{°}=0$.

D. $\sin {120}^{°}+\cos {30}^{°}=0$ .

Câu 20. Cho hai góc nhọn $\alpha$ và $\beta$ ($\alpha <\beta )$. Khẳng định nào sau đây là sai?

A. $\cos \alpha <\cos \beta$ .

B. $\sin \alpha <\sin \beta$ .

C. $\tan \alpha +\tan \beta >0$.

D. $\cot \alpha >\cot \beta$ .

Câu 21. Cho $\Delta ABC$ vuông tại A, góc B bằng ${30}^{°}$. Khẳng định nào sau đây là sai?

A. $\cos B=\frac{1}{\sqrt{3}}$.

B. $\sin C=\frac{\sqrt{3}}{2}$.

C. $\cos C=\frac{1}{2}$ .

D. $\sin B=\frac{1}{2}$

Câu 22. Tìm khẳng định sai trong các khẳng định sau:

A. $\cos {75}^{°}>\cos {50}^{°}$.

B. $\sin {80}^{°}>\sin {50}^{°}$.               

C. $\tan {45}^{°}<\tan {60}^{°}$ .

D. $\cos {30}^{°}=\sin {60}^{°}$.

Câu 23. Đẳng thức nào sau đây đúng?

A. $\tan \left({180}^{\text{o}}+a\right)=-\tan a$ .

B. $\cos \left({180}^{\text{o}}+a\right)=-\cos a$ .

C. $\sin \left({180}^{\text{o}}+a\right)=\sin a$.

D. $\cot \left({180}^{\text{o}}+a\right)=-\cot a$ .

Câu 24. Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. $\sin \left({180}^{°}-\alpha \right)=-\sin \alpha$ .

B. $\cos \left({180}^{°}-\alpha \right)=\cos \alpha$

C. $\tan \left({180}^{°}-\alpha \right)=\tan \alpha$ .

D. $\cot \left({180}^{°}-\alpha \right)=-\cot \alpha$

Câu 25. Cho $\alpha$ và $\beta$ là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?

A. $\sin \alpha =\sin \beta$.

B. $\cos \alpha =-\cos \beta$ .

C. $\tan \alpha =-\tan \beta$ .

D. $\cot \alpha =\cot \beta$ .

Câu 26. Cho góc $\alpha$ tù. Điều khẳng định nào sau đây là đúng?

A. $\sin \alpha <0$.

B. $\cos \alpha >0$ .

C. $\tan \alpha >0$ .

D. $\cot \alpha <0$ .

Câu 27. Điều khẳng định nào sau đây là đúng?

A. $\sin \alpha =-\sin \left({180}^{°}-\alpha \right)$.

B. $\cos \alpha =-\cos \left({180}^{°}-\alpha \right)$.

C. $\tan \alpha =\tan \left({180}^{°}-\alpha \right)$.

D. $cot\alpha =\cot \left({180}^{°}-\alpha \right)$.

Câu 28. Hai góc nhọn $\alpha$ và $\beta$ phụ nhau, hệ thức nào sau đây là sai?

A. $\sin \alpha =\cos \beta$ .

B. $\tan \alpha =\cot \beta$ .

C. $\cot \beta =\frac{1}{\cot \alpha }$ .

D. $\cos \alpha =-\sin \beta$.

Câu 29. Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. $\sin {150}^{°}=-\frac{\sqrt{3}}{2}$.

B. $\cos {150}^{°}=\frac{\sqrt{3}}{2}$.

C. $\tan {150}^{°}=-\frac{1}{\sqrt{3}}$.

D. $\cot {150}^{°}=\sqrt{3}$

Câu 30. Bất đẳng thức nào dưới đây là đúng?

A. $\sin {90}^{°}<\sin {100}^{°}$ .

B. $\cos {95}^{°}>\cos {100}^{°}$ .

C. $\tan {85}^{°}<\tan {125}^{°}$ .

D. $\cos {145}^{°}>\cos {125}^{°}$ .

Xem các Phương pháp giải bài tạp hay, chi tết khác: 

Tích vô hướng của hai vectơ và cách giải bài tập

Công thức góc giữa hai vectơ chi tiết nhất

Công thức Tích vô hướng của hai vectơ chi tiết nhất

Các tính chất của tích vô hướng chi tiết nhất

Công thức tính độ dài vectơ chi tiết nhất