Toptailieu.vn biên soạn và giới thiệu Công thức viết phương trình đường thẳng theo đoạn chắn (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức viết phương trình đường thẳng theo đoạn chắn (HAY NHẤT 2024)

I. Lý thuyết tổng hợp

- Cho đường thẳng d cắt trục Ox và Oy lần lượt tại hai điểm A(a; 0) và B(0; b) với $a\ne 0$, $b\ne 0$, phương trình đường thẳng d theo đoạn chắn là: $\frac{x}{a}+\frac{y}{b}=1$.

II. Các công thức

Cho đường thẳng d có:

$d\cap \text{Ox}$ tại A(a; 0)  ($a\ne 0$)

$d\cap \text{Oy}$ tại B(0; b)  ($b\ne 0$)

$\Rightarrow$ Phương trình đường thẳng d theo đoạn chắn: $\frac{x}{a}+\frac{y}{b}=1$ 

III. Ví dụ minh họa 

Bài 1: Cho đường thẳng d cắt Ox và Oy lần lượt tại A(2; 0) và B(0; 2). Viết phương trình đường thẳng d theo đoạn chắn.

Lời giải:

Biết đường thẳng d cắt Ox và Oy lần lượt tại A(2; 0) và B(0; 2).

Ta có phương trình đường thẳng d theo đoạn chắn:

$\frac{x}{2}+\frac{y}{2}=1$

Bài 2: Cho đường thẳng d cắt Ox và Oy lần lượt tại A, B. Biết M(2; 4) là trung điểm của AB. Viết phương trình đường thẳng d theo đoạn chắn.

Lời giải:

Gọi tọa độ của điểm A là A(a; 0) (do A thuộc Ox), tọa độ của điểm B là B(0; b) (do B thuộc Oy).

M(2; 4) là trung điểm của AB nên ta có:

$\left\{\begin{array}{l}\frac{a}{2}=2\\ \frac{b}{2}=4\end{array}\right.\iff \left\{\begin{array}{l}a=4\\ b=8\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}A(4;0)\\ B(0;8)\end{array}\right.$

Ta có phương trình đường thẳng d theo đoạn chắn là: $\frac{x}{4}+\frac{y}{8}=1$

Bài 3: Cho đường thẳng d cắt trục Ox, Oy lần lượt tại hai điểm A(3; 0) và điểm B(0; 5). Viết phương trình đường thẳng d theo đoạn chắn.

Lời giải:

Biết đường thẳng d cắt Ox và Oy lần lượt tại A(3; 0) và B(0; 5).

Ta có phương trình đường thẳng d theo đoạn chắn: $\frac{x}{3}+\frac{y}{5}=1$.

IV. Bài tập vận dụng

Câu 1: Phương trình đường thẳng cắt hai trục tọa độ tại A( -2 ;0) và B( 0 ; 5) là:

A. 5x - 2y - 10 = 0    B. 5x - 2y + 10 = 0    C. 2x - 5y - 10 = 0    D. 2x + 5y + 4 = 0

Lời giải

Đường thẳng AB cắt hai trục tọa độ tại A( -2 ; 0) và B( 0 ; 5) nên phương trình đường thẳng AB theo đoạn chắn là :

 = 1

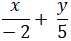
⇔ 5x - 2y + 10 = 0

Chọn B.

Câu 2: Lập phương trình đường thẳng đi qua điểm M( 5; -3) và cắt hai trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.

A. 3x - 5y - 30 = 0    B. 3x + 5y - 30 = 0    C. 5x - 3y - 34 = 0    D. 5x - 3y + 34 = 0

Lời giải

Gọi A ∈ Ox ⇒ A(x_A; 0); B ∈ Oy ⇒ B(0; y_B)

Ta có M là trung điểm AB ⇒ 

Suy ra (AB): 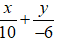 = 1 ⇔ 3x - 5y - 30 = 0.

Chọn A.

Câu 3: Có mấy đường thẳng đi qua điểm M( 2; -3) và cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB vuông cân.

A. 2    B. 3    C. 1    D. Không có.

Lời giải

Gọi tọa độ điểm A( a; 0) và B( 0; b).

Phương trình đoạn chắn (AB): 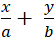 =1

Do tam giác OAB vuông cân tại O ⇔ |a| = |b| ⇔ 

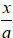
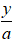
TH1: b = a ⇒  +  = 1 ⇔ x + y = a

mà M(2; -3) ∈ (AB) ⇒ 2 - 3 = a ⇔ a = -1 ⇒ b = -1

Vậy phương trình (AB) : x + y + 1= 0 .

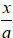
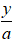
TH2: b = - a ⇒  -  = 1 ⇔ x - y = a

mà M(2; -3) ∈ (AB) ⇒ 2 + 3 = a ⇔ a = 5 ⇒ b = - 5

Vậy phương trình ( AB) : x - y - 5= 0 .

Vậy có hai đường thẳng thỏa mãn đầu bài.

Chọn A.

Câu 4: Viết phương trình đường thẳng đi qua hai điểm A(0; -3) và B(-2; 0).

A. 2x + 3y - 6 = 0    B. 3x + 2y - 6 = 0    C. 3x + 2y + 6 = 0    D. 2x - 3y - 6 = 0

Lời giải

+ Đường thẳng AB: 

=> Phương trình đoạn chắn đường thẳng AB: 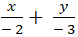 = 1

Hay (AB) : 3x + 2y + 6 = 0

Chọn C.

Câu 5: Cho đường thẳng d: x - y + 3 = 0. Viết phương trình đường thẳng d dưới dạng đoạn chắn.

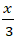
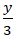
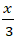
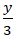
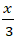
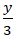
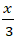
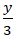
A. -  +  = 1    B.  +  = 1    C. -  -  = 1    D.  -  = 1

Lời giải

Đường thẳng d cắt trục Ox tại A(- 3; 0) và cắt trục Oy tại B(0; 3).

=> Phương trình đoạn chắn đường thẳng d:

-  +  = 1

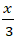
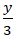
Chọn A.

Câu 6: Cho đường thẳng d: x + y - 6 = 0. Viết phương trình đường thẳng d dưới dạng phương trình đoạn chắn?

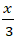
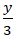
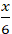
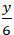
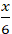
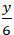
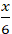
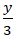
A.  -  = 1    B.  -  = 1    C.  +  = 1    D. -  -  = 1

Lời giải

Đường thẳng d cắt trục Ox tại điểm A(6;0) .

Đường thẳng d cắt trục Oy tại điểm B(0;6).

Đường thẳng d đi qua hai điểm A(6;0) và B(0; 6) nên phương trình đường thẳng d dạng đoạn chắn là: 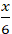 +  = 1

Chọn C.

Câu 7: Phương trình tổng quát của đường thẳng cắt hai trục tọa độ tại A( 3 ; 0) và       B(0 ; -2) là:

A. 3x - 2y + 1 = 0    B. -2x + 3y + 6 = 0    C. 2x - 3y + 6 = 0    D. 2x - 3y + 4 = 0

Lời giải

Đường thẳng AB cắt hai trục tọa độ tại A(3 ; 0) và B( 0 ; -2) nên phương trình đường thẳng AB theo đoạn chắn là :

 = 1

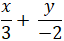
⇔ -2x + 3y + 6 = 0

Chọn B.

Câu 8: Lập phương trình đường thẳng đi qua điểm M( 1;-2) và cắt hai trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB.

A. – 4x + 2y + 8 = 0    B. 4x + 2y + 8 = 0    C. 2x - y + 1 = 0    D. 2x + y = 0

Lời giải

Gọi A (a ; 0) ∈ Ox; B(0; b) ∈ Oy

Ta có M là trung điểm AB nên :

 ⇔ a = 2 và b = - 4

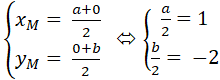
Suy ra phương trình AB : 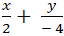 = 1 hay – 4x + 2y + 8 = 0

Chọn A.

Câu 9: Có mấy đường thẳng đi qua điểm M(3;3) và cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB vuông cân.

A. 2    B. 3    C. 1    D. Không có.

Lời giải

Gọi tọa độ điểm A( a; 0) và B( 0; b).

Phương trình đoạn chắn đường thẳng AB: 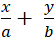 =1

Do tam giác OAB vuông cân tại O ⇔ |a| = |b| ⇔ 

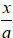
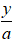
TH1: b = a ⇒  +  = 1 ⇔ x + y = a

Mà M(3;3) thuộc AB nên 3 + 3 = a ⇔ a= 6 ⇒ b= 6

Vậy phương trình (AB) : x + y - 6 = 0 .

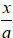
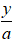
TH2: b = - a ⇒  -  = 1 ⇔ x - y = a

Mà M( 3; 3) thuộc AB nên 3 - 3= a ⇔ a= 0 ⇒ b= 0 ( loại vì khi đó 3 điểm A; B và O trùng nhau)

Vậy có một đường thẳng thỏa mãn đầu bài.

Chọn C.

Câu 10: Viết phương trình đường thẳng đi qua hai điểm A( 0; 4) và B( -3;0).

A. 4x + 3y - 6 = 0    B. 4x - 3y - 6 = 0    C. 4x - 3y + 12 = 0    D. 4x - 3y + 6 = 0

Lời giải

+ Đường thẳng AB: 

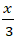
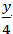
=> Phương trình đoạn chắn đường thẳng AB: -  +  = 1

Hay (AB) : 4x - 3y + 12 = 0

Chọn C.

Câu 11: Cho đường thẳng d: 2x - y + 4 = 0. Viết phương trình đường thẳng d dưới dạng đoạn chắn.

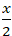
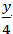
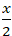
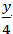
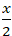
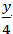
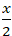
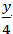
A. -  +  = 1    B.  + (-  ) = 1    C. -  -  = 1    D.  -  = 1

Lời giải

Đường thẳng d cắt trục Ox tại A(-2;0) và cắt trục Oy tại B(0; 4).

=> Phương trình đoạn chắn đường thẳng d:

-  +  = 1

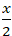
Chọn A 

V. Bài tập tự luyện 

Câu 1: Khoảng cách giữa hai đường thẳng d₁: 6x-4y+5=0 và d₂: 3x-2y+1=0 được cho bởi công thức nào sau đây?

Câu 2: Cho hai đường thẳng cắt nhau d₁: a₁x+b₁y+c₁=0 và d₂: a₂x+b₂y+c₂=0. Phương trình các phân giác góc tạo bởi d₁,d₂ là

Câu 3: Cho hai đường thẳng cắt nhau d₁: 3x-4y+1=0 và d₂: x+3=0. Phương trình các phân giác góc tạo bởi d₁,d₂ là

A. x + 2y + 7 = 0 và 2x – y + 7 = 0

B. x + 2y + 4 = 0 và 2x – y + 4 = 0

C. x + 2 y + 7 = 0 và 2x – y + 4 = 0

D. x + 2y – 7 = 0 và 2x – y – 7 = 0

Câu 4: Cho hai đường thẳng d₁:3x-4y+1=0,d₂:4x+3y+3=0. Điểm M nào sau đây cách đều hai đường thẳng trên?

A. M(1;3)     B. M(5; -1)     C. M(4; -2)     D. M(-1; 2)

Câu 5: Cho ba đường thẳng d₁:3x-4y+1=0,d₂:5x+3y-1=0,d₃:x+y+6=0. Số điểm M cách đều ba đường thẳng trên là

A. 1     B. 2     C. 3     D. 4

Câu 7: Cho điểm A(7; 4) và đường thẳng Δ: 3x – 4y + 8 = 0. Bán kính đường tròn tâm A và tiếp xúc với Δ là:

Câu 8: Cho hai đường thẳng d₁:x-3y+4=0,d₂:2x-y+3=0. Bán kính đường tròn tiếp xúc với hai đường thẳng d₁,d₂ là

Câu 9: Cho tam giác ABC, biết phương trình ba cạnh của tam giác là

AB: x – 3y – 1 = 0, BC: x + 3y + 7 = 0, CA: 5x – 2y + 1 = 0

Phương trình đường cao AH của tam giác là:

A. 13x – 39y + 9 = 0

B. 39x – 13 y + 9 = 0

C. 39x – 13y – 9 = 0

D. 39x + 13y + 9 = 0

Câu 10: Cho ba điểm A(5;2), B(1; - 4), C(3; 6). Phương trình trung tuyến AM của tam giác là:

A. x – 3y + 1 = 0

B. 3x – y + 1 = 0

C. x – y + 1 = 0

D. 3x – 3y + 1 = 0

Câu 11: Nếu m là số đường thẳng Δ có tính chất đi qua điểm M(8; 5) và cắt Ox, Oy tại A, B mà OA = OB thì

A. m = 0     B. m = 1     C. m = 2     D. m = 3

Câu 12: Cho hai đường thẳng d₁: (√3+1)x+(3-√2)y+1=0,d₂: √5 x+(4-√2)y-6=0.

Khẳng định nào sau đây là đúng?

A. Hai đường thẳng trùng nhau

B. Hai đường thẳng song song

C. Hai đường thẳng cắt nhau

D. Hai đường thẳng vuông góc với nhau

Câu 13: Cho hai đường thẳng d₁:2x+3y+1=0,d₂:mx+(2m-2)y-m+6=0. Giá trị của m để hai đường thẳng song song là

A. m =0     B. m = - 4     C. m = 4     D. không tồn tại m thỏa mãn

Câu 14: Cho ba đường thẳng d₁: 2x+3y+1=0,d₂: mx+(m-1)y-2m+1=0,d₃: 2x+y-5=0. Giá trị của m để hai đường thẳng d₁,d₂ cắt nhau tại một điểm nằm trên d₃ là:

A. m = 0     B. m = - 4     C. m = 4     D. không tồn tại giá trị m thỏa mãn

Câu 15: Cho ba đường thẳng d₁:x-2y+1=0,d₂:mx-(3m-2)y+2m-2=0,d₃:x+y-5=0. Giá trị m để hai đường thẳng d₁,d₂ cắt nhau tại một điểm nằm trên d₃ là

A. m = 0     B. m = 1     C. m = 2     D. không tồn tại m thỏa mãn

Câu 16: Cho hai đường thẳng d: (m – 2)x +(m – 6)y + m – 1= 0, Δ: (m – 4)x + (2m – 3)y – m + 5 = 0. Tất cả giá trị của m để hai đường thẳng cắt nhau là

A. m ≠ 3     B. m ≠ 6     C. m ≠ 3 và m ≠ -6     D. không có m thỏa mãn

Câu 17: Cho hình chữ nhật ABCD có đỉnh A(7; 4) và phương trình hai cạnh là:

7x – 3y + 5 = 0, 3x + 7y – 1 = 0. Diện tích hình chữ nhật ABCD là:

Câu 18: Diện tích hình vuông có bốn đỉnh nằm trên hai đường thẳng song song d₁:2x-4y+1=0 và d₂:-x+2y+10=0 là:

Câu 19: Cho tam giác ABC với A(-1; -1), B(2; -4), C(4; 3). Diện tích tam giác ABC là:

A. 3/2     B. 9/2     C. 27/2     D. 13

Câu 20: Cho hai điểm A(-4; -1), B(-2; 1). Điểm C trên đường thẳng ∆: x – 2y + 3 = 0 sao cho diện tích tam giác ABC bằng 40 (đvdt). Khi đó tung độ của điểm C là

A. – 10 hoặc 10

B. – 40 hoặc 40

C. 20

D. 50

Xem các Phương pháp giải bài tập hay, chi tiết khác:

Công thức tìm điểm đối xứng qua đường thẳng hay và chi tiết

Công thức viết phương trình đường phân giác hay chi tiết nhất

Công thức về vị trí tương đối của hai đường thẳng hay và chi tiết nhất

Công thức tính góc giữa hai đường thẳng hay, chi tiết nhất

Công thức tính khoảng cách từ một điểm đến một đường thẳng