Phương pháp giải Phương trình bậc nhất đối với sinx, cosx (HAY NHẤT 2024)

Ngọc Nguyễn Ngày: 10-08-2023 Lớp 11

405

Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Phương trình bậc nhất đối với sinx, cosx (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Nội dung bài viết

1. Lý thuyết
2. Các dạng bài tập
Dạng 1: Giải phương trình bậc nhất đối với sin và cos
Dạng 2: Tìm điều kiện để phương trình a.sinx + b.cosx = c có chứa tham số m có nghiệm
3. Bài tập vận dụng
4. Bài tập tự luyện

Phương pháp giải Phương trình bậc nhất đối với sinx, cosx (HAY NHẤT 2024)

1. Lý thuyết

- Phương trình bậc nhất đối với sin và cos có dạng: a.sinx + b.cosx = c (với a; b là các số thực, a; b khác 0).

- Điều kiện có nghiệm: $a^{2} + b^{2} \geq c^{2}$ .

2. Các dạng bài tập

Dạng 1: Giải phương trình bậc nhất đối với sin và cos

- Phương pháp giải:

Chia cả hai vế của phương trình cho $\sqrt{a^{2} + b^{2}}$ , ta được:

$\frac{a}{\sqrt{a^{2} + b^{2}}} \sin x + \frac{b}{\sqrt{a^{2} + b^{2}}} \cos x = \frac{c}{\sqrt{a^{2} + b^{2}}}$ (*)

* Đặt $\cos α = \frac{a}{\sqrt{a^{2} + b^{2}}}; \sin α = \frac{b}{\sqrt{a^{2} + b^{2}}}$ với $\cos α = \frac{a}{\sqrt{a^{2} + b^{2}}}; \sin α = \frac{b}{\sqrt{a^{2} + b^{2}}}$

Khi đó phương trình (*) đưa về dạng

$\sin x \cos α + \cos x \sin α = \frac{c}{\sqrt{a^{2} + b^{2}}}$

$\Leftrightarrow \sin (x + α) = \frac{c}{\sqrt{a^{2} + b^{2}}}$ . Đưa về phương trình lượng giác cơ bản.

* Hoặc đặt $\sin α = \frac{a}{\sqrt{a^{2} + b^{2}}}; \cos α = \frac{b}{\sqrt{a^{2} + b^{2}}}$ với $α \in [0; 2 π)$

Khi đó phương trình (*) đưa về dạng

$\sin x \sin α + \cos x \cos α = \frac{c}{\sqrt{a^{2} + b^{2}}}$

$\Leftrightarrow \cos (x - α) = \frac{c}{\sqrt{a^{2} + b^{2}}}$ . Đưa về phương trình lượng giác cơ bản.

* Phương trình có nghiệm khi

$0 \leq |\frac{c}{\sqrt{a^{2} + b^{2}}}| \leq 1 \Leftrightarrow |c| \leq \sqrt{a^{2} + b^{2}} \Leftrightarrow c^{2} \leq a^{2} + b^{2}$ .

Chú ý: Các công thức đặc biệt

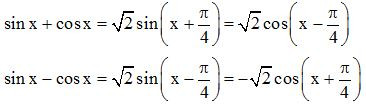
Phương trình bậc nhất đối với sinx, cosx và cách giải – Toán lớp 11 (ảnh 1)

- Ví dụ minh họa:

Ví dụ 1: Giải các phương trình sau:

a) $\sin 4 x + \sqrt{3} \cos 4 x = \sqrt{2}$

b) 5sin2x +12cos2x = 13

c) sin²x - 2cosxsinx + 1 = 0

Lời giải

a) $\sin 4 x + \sqrt{3} \cos 4 x = \sqrt{2}$

$\Leftrightarrow \frac{1}{2} \sin 4 x + \frac{\sqrt{3}}{2} \cos 4 x = \frac{\sqrt{2}}{2}$ (1)

Đặt $\cos \frac{π}{3} = \frac{1}{2}; \sin \frac{π}{3} = \frac{\sqrt{3}}{2}$

Khi đó (1) $\Leftrightarrow \sin 4 x \cos \frac{π}{3} + \cos 4 x \sin \frac{π}{3} = \frac{\sqrt{2}}{2}$

$\Leftrightarrow \sin (4 x + \frac{π}{3}) = \frac{\sqrt{2}}{2}$

$\Leftrightarrow [\begin{array}{l} 4 x + \frac{π}{3} = \frac{π}{4} + k 2 π \\ 4 x + \frac{π}{3} = π - \frac{π}{4} + k 2 π \end{array}$

$\Leftrightarrow [\begin{array}{l} 4 x = - \frac{π}{12} + k 2 π \\ 4 x = \frac{5 π}{12} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = - \frac{π}{48} + \frac{k π}{2} \\ x = \frac{5 π}{48} + \frac{k π}{2} \end{array} (k \in ℤ)$

Vậy họ nghiệm của phương trình là: $x = - \frac{π}{48} + \frac{k π}{2}; x = \frac{5 π}{48} + \frac{k π}{2}; k \in ℤ$ .

b) $5 \sin 2 x + 12 \cos 2 x = 13$

$\Leftrightarrow \frac{5}{13} \sin 2 x + \frac{12}{13} \cos 2 x = 1$ (2)

Đặt $\cos α = \frac{5}{13}; \sin α = \frac{12}{13}$ với $α \in [0; 2 π)$

Khi đó (2) $\Leftrightarrow \sin 2 x \cos α + \cos 2 x \sin α = 1$

$\Leftrightarrow \sin (2 x + α) = 1 \begin{array}{l} \Leftrightarrow 2 x + α = \frac{π}{2} + k 2 π (k \in ℤ) \\ \Leftrightarrow 2 x = - α + \frac{π}{2} + k 2 π (k \in ℤ) \\ \Leftrightarrow x = - \frac{α}{2} + \frac{π}{4} + k π (k \in ℤ) \end{array}$

Vậy họ nghiệm của phương trình là: $x = - \frac{α}{2} + \frac{π}{4} + k π; k \in ℤ$ với $\cos α = \frac{5}{13}; \sin α = \frac{12}{13}$ .

c) sin²x - 2cosxsinx + 1 = 0

$\begin{array}{l} \Leftrightarrow \frac{1 - \cos 2 x}{2} - \sin 2 x + 1 = 0 \\ \Leftrightarrow 1 - \cos 2 x - 2 \sin 2 x + 2 = 0 \\ \Leftrightarrow \cos 2 x + 2 \sin 2 x = 3 \end{array}$

Ta thấy: 1² + 2² < 3². Vậy phương trình trên vô nghiệm.

Ví dụ 2: Giải các phương trình sau:

a) $3 \sin 3 x - \sqrt{3} \cos 9 x = 1 + 4 \sin^{3} 3 x$

b) $\cos 3 x - \sin 5 x = \sqrt{3} (\cos 5 x - \sin 3 x)$

Lời giải

a) $3 \sin 3 x - \sqrt{3} \cos 9 x = 1 + 4 \sin^{3} 3 x$

$\begin{array}{l} \Leftrightarrow 3 \sin 3 x - 4 \sin^{3} 3 x - \sqrt{3} \cos 9 x = 1 \\ \Leftrightarrow \sin 9 x - \sqrt{3} \cos 9 x = 1 \\ \Leftrightarrow \frac{1}{2} \sin 9 x - \frac{\sqrt{3}}{2} \cos 9 x = \frac{1}{2} \\ \Leftrightarrow \sin 9 x . \cos \frac{π}{3} - \cos 9 x . \sin \frac{π}{3} = \frac{1}{2} \end{array}$
$\begin{array}{l} \Leftrightarrow \sin (9 x - \frac{π}{3}) = \frac{1}{2} \\ \Leftrightarrow [\begin{array}{l} 9 x - \frac{π}{3} = \frac{π}{6} + k 2 π \\ 9 x - \frac{π}{3} = π - \frac{π}{6} + k 2 π \end{array} \\ \Leftrightarrow [\begin{array}{l} 9 x = \frac{π}{2} + k 2 π \\ 9 x = \frac{7 π}{6} + k 2 π \end{array} \\ \Leftrightarrow [\begin{array}{l} x = \frac{π}{18} + \frac{k 2 π}{9} \\ x = \frac{7 π}{54} + \frac{k 2 π}{9} \end{array}, (k \in ℤ) \end{array}$

Vậy họ nghiệm của phương trình là: $x = \frac{π}{18} + \frac{k 2 π}{9}$ ; $x = \frac{7 π}{54} + \frac{k 2 π}{9}$ $(k \in ℤ)$

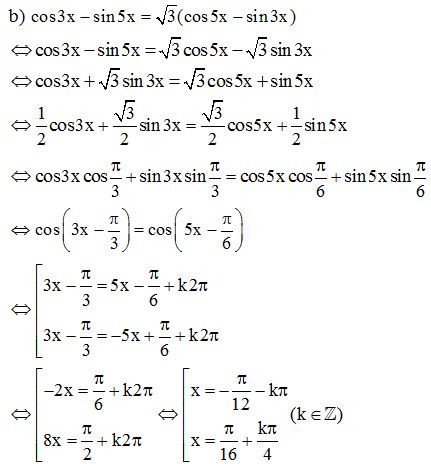
Phương trình bậc nhất đối với sinx, cosx và cách giải – Toán lớp 11 (ảnh 1)

Vậy họ nghiệm của phương trình là: $x = - \frac{π}{12} - k π; x = \frac{π}{16} + \frac{k π}{4}; k \in ℤ$ .

Dạng 2: Tìm điều kiện để phương trình a.sinx + b.cosx = c có chứa tham số m có nghiệm

- Phương pháp giải:

Điều kiện có nghiệm: $a^{2} + b^{2} \geq c^{2}$ .

- Ví dụ minh họa:

Ví dụ 1: Tìm m để phương trình: (m-1)cosx + 2sinx = m+3 có nghiệm.

Lời giải

Để phương trình có nghiệm: ${(m - 1)}^{2} + 2^{2} \geq {(m + 3)}^{2}$

$\begin{array}{l} \Leftrightarrow m^{2} - 2 m + 1 + 4 \geq m^{2} + 6 m + 9 \\ \Leftrightarrow - 8 m \geq 4 \Leftrightarrow m \leq - \frac{1}{2} \end{array}$

Vậy $m \leq - \frac{1}{2}$ thì phương trình (m-1)cosx + 2sinx = m+3 có nghiệm.

Ví dụ 2: Tìm m để phương trình: (m-1)sinx + mcosx = m+1 có nghiệm.

Lời giải

Để phương trình có nghiệm: ${(m - 1)}^{2} + m^{2} \geq {(m + 1)}^{2}$

$\begin{array}{l} \Leftrightarrow m^{2} - 2 m + 1 + m^{2} \geq m^{2} + 2 m + 1 \\ \Leftrightarrow m^{2} - 4 m \geq 0 \\ \Leftrightarrow m (m - 4) \geq 0 \\ \Leftrightarrow [\begin{array}{l} \{\begin{cases} m \geq 0 \\ m - 4 \geq 0 \end{cases} \\ \{\begin{cases} m \leq 0 \\ m - 4 \leq 0 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} \{\begin{cases} m \geq 0 \\ m \geq 4 \end{cases} \\ \{\begin{cases} m \leq 0 \\ m \leq 4 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} m \geq 4 \\ m \leq 0 \end{array} \end{array}$

Vậy $m \geq 4$ hoặc $m \leq 0$ thì phương trình (m-1)sinx + mcosx = m+1 có nghiệm.

3. Bài tập vận dụng

Câu 1. Họ nghiệm của phương trình $\sqrt{3} \sin 2 x - \cos 2 x + 1 = 0$ là:

A. $[\begin{array}{l} x = k π \\ x = \frac{π}{3} + k π \end{array} (k \in ℤ)$

B. $[\begin{array}{l} x = k π \\ x = \frac{2 π}{3} + 2 k π \end{array} (k \in ℤ)$

C. $[\begin{array}{l} x = 2 k π \\ x = \frac{2 π}{3} + 2 k π \end{array} (k \in ℤ)$

D. $[\begin{array}{l} x = k π \\ x = \frac{2 π}{3} + k π \end{array} (k \in ℤ)$

Câu 2. Có bao nhiêu nghiệm thuộc khoảng $(0; 2 π)$ của phương trình cos4x – sin4x = 1?

A. 5

B. 3

C. 6

D. 7

Câu 3. Họ nghiệm của phương trình: $\sin 3 x - \sqrt{3} \cos 3 x = 2 \cos 5 x$ là:

A. $[\begin{array}{l} x = \frac{5 π}{48} + \frac{k π}{5} \\ x = - \frac{5 π}{12} - k π \end{array} (k \in ℤ)$

B. $[\begin{array}{l} x = \frac{5 π}{48} + \frac{k π}{4} \\ x = - \frac{5 π}{12} - k 2 π \end{array} (k \in ℤ)$

C. $[\begin{array}{l} x = \frac{5 π}{48} + \frac{k π}{4} \\ x = - \frac{5 π}{12} - k \frac{π}{2} \end{array} (k \in ℤ)$

D. $[\begin{array}{l} x = \frac{5 π}{48} + \frac{k π}{4} \\ x = - \frac{5 π}{12} - k π \end{array} (k \in ℤ)$

4. Bài tập tự luyện

Câu 1: Giải phương trình : sinx + cosx= √2

A. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn A.

Câu 2: Giải phương trình : √3 sinx- √3 cosx=0?

A. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn C.

Câu 3: Giải phương trình: √6 sinx- √2 cosx=2

A. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn D.

Câu 4: Một họ nghiệm của phương trình : 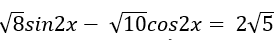Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11 là:

A. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. x= Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. Tất cả sai.

Lời giải:

Phương trình : 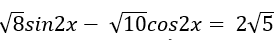Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11 là phương trình bậc nhất đối với sinx và cosx và (〖√8)²+ (√10)² < (2√5)²

⇒ Phương trình đã cho vô nghiệm.

Chọn D.

Câu 5: Giải phương trình: Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

A. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn B.

Câu 6: Giải phương trình: Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

A. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D.Tất cả sai

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn A

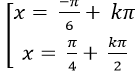
Câu 7: Giải phương trình: Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

A. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn C.

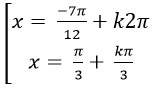
Câu 8: Giải phương trình: Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

A. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn A

Xem thêm Phương pháp giải các dạng bài tập hay, chi tiết khác:

Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết

Công thức giải phương trình lượng giác cơ bản

Công thức, cách biến đổi biểu thức a sinx + b cosx

Công thức, cách gộp nghiệm phương trình lượng giác

Quy tắc đếm và cách giải các dạng bài tập

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Chọn C.

Câu 3:Giải phương trình: √6 sinx- √2 cosx=2

A. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

B. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

C. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

D. Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Lời giải:

Giải phương trình bậc nhất đối với sinx và cosx - Toán lớp 11

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

398

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

430

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

431

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

387