Công thức chỉnh hợp (50 bài tập minh họa) HAY NHẤT 2024

Ngọc Nguyễn Ngày: 12-08-2023 Lớp 11

334

Toptailieu.vn biên soạn và giới thiệu Công thức chỉnh hợp (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức chỉnh hợp (50 bài tập minh họa) HAY NHẤT 2024

1. Tổng hợp lý thuyết

- Cho tập hợp A có n phần tử và cho số nguyên k, ( $1 \leq k \leq n$ ). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).

- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: $A_{n}^{k} = \frac{n!}{(n - k)!}$ .

- Một số quy ước: $0! = 1, A_{n}^{0} = 1, A_{n}^{n} = n!$

- Đặc điểm: Đây là sắp xếp có thứ tự và số phần tử được sắp xếp là k: $0 \leq k \leq n$ .

2. Công thức tính

Công thức chỉnh hợp: $A_{n}^{k} = \frac{n!}{(n - k)!}$

3. Ví dụ minh họa

Ví dụ 1: Một đôi bóng có 11 cầu thủ, chuẩn bị đá penalty. Huấn luận viên muốn chọn ra 5 cầu thủ lần lượt lên đá penalty. Biết cả 11 cầu thủ đều có khả năng đá như nhau. Hỏi có bao nhiêu cách chọn cầu thủ lên đá bóng.

Lời giải

Số cách chọn và sắp xếp 5 cầu thủ lần lượt lên đá penalty là $A_{11}^{5} = 55440$ cách.

Ví dụ 2: Từ các chữ số từ 0 đến 9. Có bao nhiêu cách lập một số tự nhiên sao cho:

a) Số có 6 chữ số khác nhau

b) Số có 6 chữ số khác nhau và chia hết cho 10

c) Số lẻ có 6 chữ số khác nhau

Lời giải

a) Lập số có 6 chữ số khác nhau

Chọn chữ số đầu tiên từ các số từ 1 đến 9: có 9 cách chọn

Các chữ số còn lại là chỉnh hợp chập 5 của 9 số còn lại (khác chữ số đầu tiên) có $A_{9}^{5}$

Vậy có $9 A_{9}^{5} = 136080$ số.

b) Số có 6 chữ số khác nhau và chia hết cho 10

Chọn chữ số hàng đơn vị: có 1 cách chọn là chữ số 0

Chọn các chữ số còn lại là chỉnh hợp chập 5 của 9 số còn lại (khác chữ số 0) có $A_{9}^{5}$

Vậy có $A_{9}^{5} = 15120$ số.

c) Gọi số $\bar{a b c d e f}$ là số lẻ có 6 chữ số khác nhau được lập từ chữ số 0 đến 9

Vì $\bar{a b c d e f}$ là số lẻ nên $f \in \{1; 3; 5; 7; 9\}$

Chọn f: có 5 cách chọn

Chọn a từ các chữ số {1; 2; 3; 4; 5; 6; 7; 8; 9}\{f}: có 8 cách chọn

Chọn b, c, d, e là chỉnh hợp chập 4 của 8 chữ số còn lại (khác f và a): có $A_{8}^{4}$

Vậy có $5.8 A_{8}^{4} = 67200$ số.

4. Bài tập vận dụng

Câu 1 : Một thầy giáo có 5 cuốn sách Toán; 6 cuốn sách văn và 7 cuốn sách Anh; đôi một khác nhau. Thầy giáo muốn tặng 6 cuốn sách cho 6 học sinh. Hỏi thầy giáo có bao nhiêu cách tặng nếu thầy chỉ muốn tặng hai thể loại

A.322640 B.665280 C.1235520 D.2233440

Hướng dẫn giải :

Đáp án : D

Tặng hai thể loại Toán, Văn có 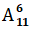Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách

Tặng hai thể loại Toán, Anh Văn có 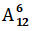Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách

Tặng hai thể loại Văn, Anh Văn có 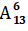Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách

Số cách tặng: 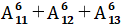Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) =2233440

Câu 2 : Có bao nhiêu cách chọn và sắp thứ tự 5 cầu thủ để đá bóng luân lưu 11m. Biết rằng cả 11 cầu thủ đều có khả năng như nhau.

A.55440 B.20680 C.32450 D.41380

Hướng dẫn giải :

Đáp án : A

Mỗi cách chọn và sắp thứ tự 5 cầu thủ để đá bóng luân lưu 11 m có thể xem là một chỉnh hợp chập 5 của tập hợp 11 cầu thủ.

⇒ Số cách chọn thỏa mãn đầu bài là:

Số cách tặng: 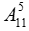Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .

Câu 3: Một lớp có 50 học sinh. Hỏi có bao nhiêu cách phân công 3 học sinh để làm vệ sinh lớp học trong một ngày?

A.117600 B.128500 C.37600 D.24360

Hướng dẫn giải :

Đáp án : A

Số cách phân công 3 học sinh để làm vệ sinh lớp học là một chỉnh hợp của chập 3 của tập hợp có 50 học sinh. Nên số cách phân công là: Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

Câu 4: Có 3 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

A.200 B.30 C.300 D.120

Hướng dẫn giải :

Đáp án : D

Cố định 3 tem thư xếp theo hàng ngang từ trái sang phải là các vị trí 1, 2, 3.

Rõ ràng nếu có 3 bì thư thì mỗi thứ tự xếp 3 bì thư này từ trái sáng phải cũng chính là cách dán.

Số cách làm cần tìm là:

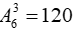
Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

Câu 5 : Có 5 nam và 6 nữ xếp thành một hàng dọc sao cho đầu hàng và cuối hàng luôn là nam. Hỏi có bao nhiêu cách xếp?

A.3628800 B.806400 C.7257600 D.151200

Hướng dẫn giải :

Đáp án : C

+ Số cách chọn 2 bạn nam xếp ở vị trí đầu hàng và cuối hàng là: Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

(ở đây ta xem cách xếp 1 bạn nam A ở đầu hàng, bạn nam B ở cuối hàng với cách xếp bạn nam A ở cuối hàng, bạn nam B ở đầu hàng là khác nhau).

+ Lúc này, còn lại 3 bạn nam và 6 bạn nữ, số cách xếp 9 người này vào 1 hàng là: 9!.

+ Vậy số cách xếp thỏa yêu cầu đề là: 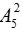Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .9! = 7257600 cách

Câu 6 : Có 5 học sinh nam và 3 học sinh nữ xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp để 2 học sinh nam xen giữa 3 học sinh nữ? (đổi 2 học sinh bất kì được cách mới)

A.2880 B.5760 C.1440 D.4320

Hướng dẫn giải :

Đáp án : A

+ Xếp cố định 3 học sinh nữ vào hàng trước, có 3! cách xếp.

+ Chọn 2 học sinh nam bất kì cho vào 2 khoảng trống nằm giữa 3 học sinh nữ, số cách chọn là Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

+ Xem nhóm 5 học sinh này là 1 học sinh, lúc này còn 3 học sinh nam vậy là ta đang có 4 học sinh. Số cách xếp 4 học sinh này thành hàng dọc là 4!.

Vậy số cách xếp cần tìm là: 3!.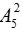 Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .4! = 2880

Câu 7 : Cho 6 thẻ đen khác nhau và 4 thẻ trắng khác nhau. Hỏi có bao nhiêu cách xếp thành một hàng sao cho không có 2 thẻ trắng nào cạnh nhau?

A.288000 B.604800 C.576000 D.14400

Hướng dẫn giải :

Đáp án : B

+ Xếp 6 thẻ đen vào 6 vị trí có 6! Cách.

+ Khi đó; có 7 khoảng trống giữa hai thẻ đen và vị trí đầu tiên; cuối cùng. Xếp 4 thẻ trắng vào 7 vị trí này có : 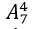Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách.

+ Số cách xếp thỏa mãn đầu bài là: 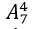Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) . 6!= 604800

Câu 8 : Một cửa hàng có 3 gói bim bim và 5 gói mì ăn liền cần xếp vào giá. Hỏi có bao nhiêu cách xếp sao cho đầu hàng và cuối hàng cùng một loại?

A.14400 B.17620 C.18720 D.40320

Hướng dẫn giải :

Đáp án : C

Đối với bài toán ta xét 2 trường hợp:

- Đầu hàng và cuối hàng đều là gói bim bim:

+ Số cách chọn 2 gói bim bim xếp ở vị trí đầu hàng và cuối hàng là: Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

+ Lúc này, ta còn lại 1 gói bim bim và 5gói mì ăn liền, số cách xếp 6 món đồ này vào 1 hàng là: 6!.

+ Vậy số cách xếp thỏa yêu cầu đề là: 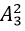Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .6!

- Đầu hàng và cuối hàng đều là cốc mì ăn liền:

+ Số cách chọn 2 gói mì ăn liền xếp ở vị trí đầu hàng và cuối hàng là: Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

+ Lúc này, còn lại 3 gói mì ăn liền và 3 gói bim bim, số cách xếp 6 người này vào 1 hàng là: 6!.

Vậy số cách xếp thỏa yêu cầu đề là: 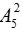Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .6!

Số cách xếp tất cả là : Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

5. Bài tập tự luyện

A.156000 B.72000 C.13363800 D.Tất cả

Lời giải:

Đáp án : C

+ Số cách tặng 6 cuốn sách bất kì là: 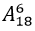Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách

+ Số cách tặng hết sách Toán 5!.13=1560

+ Số cách tặng hết sách Văn: 6!=720

+ Số cách tặng thỏa yêu cầu bài toán: 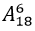Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) -1560-720=13363800

Câu 2 : Có 6 học sinh và 3 thầy giáo A,B,C. Hỏi có bao nhiêu cách xếp chỗ cho 9 người đó ngồi trên một hàng ngang có 9 ghế sao cho mỗi thầy giáo ngồi giữa hai học sinh?

A.43200 B.720 C.60 D.4320

Lời giải:

Đáp án : A

Ta sử dụng phương pháp tạo "vách ngăn".

Bước 1: Xếp vị trí cho 6 học sinh có 6! cách.

Bước 2: Do đề yêu cầu mỗi thầy giáo ngồi giữa hai học sinh nên ta chỉ tính 5 vách ngăn được tạo ra giữa 6 học sinh. Số cách xếp 3 thầy giáo vào 5 vị trí là 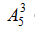Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách.

Vậy theo quy tắc nhân thì có 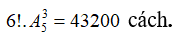Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách.

Câu 3 : Cho một hộp 10 viên bi gồm 6 bi xanh và 4 bi vàng (mỗi viên bi có kích thước khác nhau). Hỏi có bao nhiêu cách xếp 10 viên bi vào hộp thành một hàng ngang sao cho không có bi vàng nào cạnh nhau?

A.604800 B.86400 C.34560 D.3594240

Lời giải:

Đáp án : A

+ Xếp 6 viên bi xanh có 6! cách xếp. Khi đó 6 viên bi xanh sẽ tạo thành 7 chỗ trống.

+ Xếp 4 viên bi vàng vào 7 chỗ trống đó là 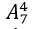Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách.

Do đó có 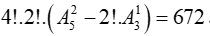Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .6!=604800 cách xếp.

Câu 4 : Trên mặt phẳng cho 5 điểm phân biệt A, B, C, D, E. Hỏi có bao nhiêu vectơ khác vectơ – không, mà có điểm đầu và điểm cuối là các điểm đã cho ?

A.10 B.120 C.20 D.25

Lời giải:

Đáp án : C

Mỗi vecto có điểm đầu và điểm cuối là các điểm đã cho là một chỉnh hợp chập 2 của 5 phần tử. Nên số vecto thỏa mãn đầu bài là : 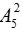Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) =20 vecto thỏa mãn.

Câu 5 : Có 6 học sinh lớp 11 và 3 học sinh lớp 12 sẽ ngồi trên một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách xếp chỗ ngồi cho 9 học sinh đó sao cho mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11?

A.144 B.6 C.14400 D.20

Lời giải:

Đáp án : C

+ Ta xếp 6 học sinh lớp 11 vào 6 ghế có 6! Cách xếp.

+ Sau khi xếp 6 học sinh lớp 11 sẽ tạo ra 5 vách ngăn- khoảng trống ( không tính vị trí đầu tiên; cuối cùng). Khi đó; ta xếp 3 học sinh lớp 12 vào 5 vị trí đó: có 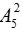Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách.

+ Áp dụng quy tắc nhân; có số cách xếp thỏa mãn đầu bài là:

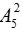
Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .6!= 14400 cách

Câu 6 : Cho 5 thẻ đen khác nhau và 3 thẻ trắng khác nhau. Hỏi có bao nhiêu cách xếp thành một hàng sao cho không có 2 thẻ trắng nào cạnh nhau?

A.2880 B.4320 C.5760 C.14400

Lời giải:

Đáp án : D

+ Xếp 5 thẻ đen có 5! cách xếp. Khi đó 5 thẻ đen tạo thành 6 chỗ trống.

+ Xếp 3 thẻ trắng vào 6 chỗ trống có 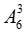Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) cách

+ Do đó có 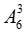Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .5! = 14400 cách xếp

Câu 7 : Trong một buổi chụp ảnh của trường A, có 5 giáo viên Toán, 3 giáo viên Hóa và 1 giáo viên Vật Lí xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp để 3 giáo viên Hóa và 1 giáo viên Vật Lí không ai cạnh nhau?

A.43200 B.35664 C.357120 D.Đáp án khác

Lời giải:

Đáp án : A

+ Xếp cố định 5 giáo viên Toán trên hàng, có 5! cách xếp.

+ Khi đó; sẽ có tất cả 6 khoảng trống gồm khoảng trống giữa 2 giáo viên Toán và vị trí đầu hàng, cuối hàng.

+ Xếp 4 giáo viên còn lại vào các khoảng trống sao cho mỗi khoảng trống chỉ chứa 1 giáo viên. Số cách xếp 4 giáo viên này là 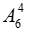Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .

Vậy số cách xếp cần tìm là: 5!.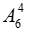 Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) =43200

Câu 8 : Có 8 bạn nam và 2 bạn nữ. Hỏi có bao nhiêu cách sắp xếp các bạn trên thành một hàng ngang sao cho hai bạn nữ đứng cách nhau đúng hai bạn nam?

A.725760 B.564480 C.757260 D.546640

Lời giải:

Đáp án : B

+ Xếp 2 bạn nữ đứng trước, số cách là 2!.

+ Sau đó chọn 2 bạn nam chen vào giữa 2 bạn nữ, số cách xếp 2 bạn nam và là 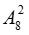Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .

+ Xem 4 bạn này là 1 bạn, khi đó ta còn lại 6 bạn nam. Số cách xếp 7 bạn này là 7!.

Vậy số cách xếp tất cả là: 2!.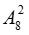 Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .7! = 564480

Câu 9 : Có 7 nam 5 nữ xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp sao cho 2 vị trí đầu và cuối là nam và không có 2 nữ nào đứng cạnh nhau?

A.118540800 B.152409600 C.12700800 D.3628800

Lời giải:

Đáp án : D

+ Số cách chọn 2 nam đứng ở đầu và cuối là: 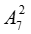Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .

+ Lúc này còn lại 5 nam và 5 nữ, để đưa 10 người này vào hàng thì trước tiên sẽ cho 5 nam đứng riêng thành hàng ngang, số cách đứng là 5!.

+ Sau đó lần lượt cho 5 nữ vào các khoảng trống ở giữa hoặc đầu, hoặc cuối của hàng 5 nam này, mỗi khoảng trống chỉ cho tối đa 1 nữ ; có tất cả 6 khoảng trống nên số cách xếp vào là 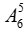Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .

+ Số cách xếp 10 người này thành hàng ngang mà 2 nữ bất kì không đứng cạnh nhau là: 5!. Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải)

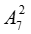
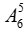
+ Đưa 10 người này vào giữa 2 nam đầu và cuối đã chọn, số cách xếp là: Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) .5!. = 3268800 cách.

Câu 10 : Lớp 10 A2 có 17 học sinh nữ và 21 học sinh nam. Giáo viên chủ nhiệm cần chọn ra 3 làm lớp trưởng; phó bí thư và lớp phó. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn.

A.37 B.50653 C.50616 D.340

Lời giải:

Đáp án : C

Với mỗi cách chọn ra ba học sinh để làm lớp trưởng; phó bí thư và lớp phó là một chỉnh hợp chập 3 của 38 phần tử (lớp có 17+21= 38 học sinh). Nên số cách chọn ra 3 bạn làm ban cán sự lớp là: 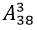Phương pháp giải bài tập Chỉnh hợp (cực hay có lời giải) = 50616 cách.