Toptailieu.vn biên soạn và giới thiệu Công thức tìm số hạng tổng quát của cấp số cộng (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:
Công thức tìm số hạng tổng quát của cấp số cộng (50 bài tập minh họa) HAY NHẤT 2024
1. Lý thuyết
a) (un) là cấp số cộng khi (d gọi là công sai)
b) Số hạng tổng quát của cấp số cộng (un) được xác định bởi công thức:
un = u1 + (n – 1)d với .
2. Công thức
Số hạng tổng quát của cấp số cộng (un) được xác định bởi công thức:
un = u1 + (n – 1)d với .
3. Ví dụ minh họa
Ví dụ 1: Cho cấp số cộng (un) có u1 = 1 và d = – 3.
a) Xác định số hạng tổng quát của cấp số cộng.
b) Tìm số hạng thứ 2021 của cấp số cộng.
c) Số – 488 là số hạng thứ bao nhiêu của cấp số cộng.
Lời giải
a) Số hạng tổng quát:
un = u1 + (n – 1)d = 1 + (n – 1).(– 3) = – 3n + 4.
b) Số hạng thứ 2021 của cấp số cộng:
u2021 = – 3.2021 + 4 = – 6059.
c) Gọi số hạng thứ k là số – 488, ta có: uk = – 3k + 4 = – 488. Suy ra k = 164.
Vậy số – 488 là số hạng thứ 164.
Ví dụ 2: Cho cấp số cộng (un) thỏa mãn .
a) Tìm u1; d?
b) Xác định số hạng tổng quát của cấp số cộng.
c) Số –1372,5 là số hạng thứ bao nhiêu của cấp số cộng.
Lời giải
a) Ta có:
Vậy .
b) Số hạng tổng quát:
c) Gọi số hạng thứ k là số – 1372,5, ta có:
.
Vậy số – 1372,5 là số hạng thứ 200.
4. Bài tập vận dụng
Câu 1: Cho cấp số cộng (un) có u1 = 0,4 và công sai d = 1. Số hạng thứ 10 của cấp số cộng này là:
A. 1,6 B. 1,4 C. 10,4 D. 9,4
Hướng dẫn giải:
Số hạng tổng quát của cấp số cộng (un) là: un = u1 + (n − 1) d
=>số hạng thứ 10 của cấp số cộng là:
u10 = 0,4 +(10 − 1) . 1 = 9,4
Chọn D.
Câu 2: Cho cấp số cộng (un) có u3 = −15 và u14 = 18. Tìm u1, d của cấp số cộng?
A. u1 = −21; d = 3 B. u1 = −20; d = 2
C. u1 = −21; d = −3 D. u1 = −20 ; d = −2
Hướng dẫn giải:
Ta có:
Từ giả thiết suy ra:
Chọn A.
Câu 3: Cho cấp số cộng ( un) thỏa mãn : 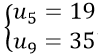
A. 39 B.27
C. 36 D.42
Hướng dẫn giải:
Theo giả thiết ta có:
=> Số hạng thứ 10 của cấp số cộng là :
u10 = u1 + 9d = 3 + 9 . 4 = 39
Chọn A.
Câu 4: Cho cấp số cộng (un) thỏa mãn điều kiện: 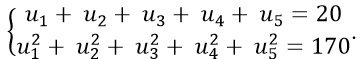
A.d = ±1 B.d = ±2 C .d = ±3 D. d = ±4
Hướng dẫn giải:
Theo đề bài ta có:
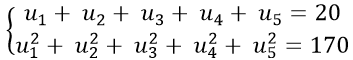
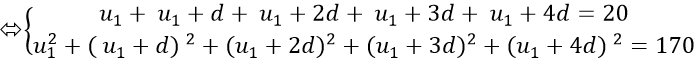
Từ (1) suy ra: u1 + 2d = 4 ⇔ u1 = 4 − 2d thế vào (2) ta được:
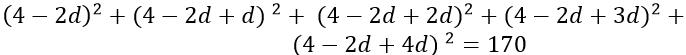
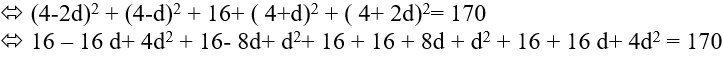
* Với d = 3 => u1 = 4 − 6 = −2
* Với d = −3 => u1 = 4 + 6 = 10
Chọn C.
Câu 5: Cho dãy số (un) với un = 7 − 2n. Khẳng định nào sau đây là sai?
A. 3 số hạng đầu của dãy u1 = 5; u2 = 3 và u3 = 1.
B. Số hạng thứ n + 1 là un+1 = 8 − 2n.
C. Là cấp số cộng có d = −2.
D. Số hạng thứ 4: u4 = −1.
Hướng dẫn giải:
* Ta có:
=> đáp án A, D đúng.
*Số hạng thứ n+1 là: un + 1 = 7 − 2(n+1) = 5 − 2n
=> B sai.
* Xét hiệu: un+1 − un = (5−2n) − (7 − 2n)= −2
=> (un) là cấp số cộng với công sai d = −2.
=> C đúng.
Câu 6: Cho một cấp số cộng có u1 = −1 và u5 = 11. Tìm công sai của cấp số cộng ?
A. d= 3 B. d= 5 C. d= 4 D. d= 2
Hướng dẫn giải:
Ta có: u5 = u1 + (5−1)d
=> 11 = − 1 + 4d ⇔ d= 3
Chọn A.
Câu 7: Cho một cấp số cộng có u1 = 10; u7 = −8. Tìm d?
A. d= −2 B. d = −3 C. d = 2 D.d = 3
Hướng dẫn giải:
Ta có: u7 = u1 +(7−1)d
=> −8 = 10 + 6d
⇔ −18 = 6d nên d = −3
Chọn B.
Câu 8: Cho cấp số cộng (un) thỏa mãn : 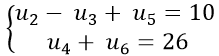
A.99 B.100
C.101 D.103
Hướng dẫn giải:
Theo giả thiết ta có:
Ta có : 301 = 1 + (n − 1) . 3 ⇔ 300 = 3(n-1)
⇔ n − 1 = 100 ⇔ n = 101
Vậy 301 là số hạng thứ 101 của cấp số cộng.
Chọn C.
Câu 9: Cho cấp số cộng (un) thỏa mãn 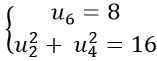
A.8 B.10
C. 6 D. 12
Hướng dẫn giải:
Theo giả thiết ta có :
Từ (1) suy ra : u1 = 8 − 5d thay vào (2) ta được :
Với
Số hạng thứ 6 là:
Với d = 2 => u1 = −2
Số hạng thứ 6: u6 = −2 + 5 . 2 = 8
Chọn A.
Câu 10: Cho cấp số cộng (un) có u1 = −2 và công sai d = 3. Hỏi có bao nhiêu số hạng của cấp số thỏa mãn un < 11.
A.3 B. 4 C.5 D.6
Hướng dẫn giải:
Cấp số cộng có u1 = −2 và công sai d = 3 nên số hạng tổng quát của cấp số cộng là:
un = u1 + (n − 1) . d = −2 + 3(n − 1) = 3n − 5
Để un < 11 thì 3n − 5 < 11
Mà n nguyên dương nên n ∈ { 1,2,3,4,5}
Vậy có 5 số hạng của cấp số cộng thỏa mãn điều kiện
Chọn C.
Câu 11: Viết ba số xen giữa các số 2 và 22 để được cấp số cộng có 5 số hạng. Tính tổng của ba số hạng xen giữa đó.
A. 36 B.28 C. 32 D.30
Hướng dẫn giải:
Khi viết ba số xen giữa hai số 2 và 22 để được cấp số cộng có 5 số hạng thì:
u1 = 2 và u5 = 22.
+ Lại có: u5 = u1 + (5 − 1) d nên 22 = 2 + 4d
⇔ 20 = 4d ⇔ d= 5
+Suy ra: u2 = u1 + d = 2 + 5= 7
u3 = u1 + 2d = 2 + 2 . 5 = 12
Và u4 = u1 + 3d = 2 + 3 . 5 = 17
=> u2 + u3 +u4 = 7 + 12 + 17 = 36
Chọn A.
5. Bài tập tự luyện
Câu 1: Cho (un) là cấp số cộng thỏa mãn : 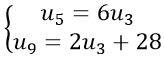
A.67 B.75
C. 87 D. 91
Câu 2: Tìm ba số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng −9 và tổng các bình phương của chúng bằng 29.
A. 0 ; −3 ; −6 B. −2 ; −3 ; −4
C. −1; −2 ; −3 D. −3 ; −2 ; −1
Câu 3: Cho dãy số (un) là cấp số cộng thỏa mãn: 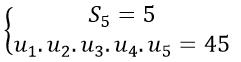
A.3 hoặc −1 B. 2 hoặc −2.
C.2 hoặc −3 D. −2 hoặc 1.
Câu 4: Cho 2 cấp số cộng : 5 ;8 ;11 ; .....và 3 ;7 ;11,.... Hỏi trong 100 số hạng đầu tiên của mỗi cấp số ; có bao nhiêu số hạng chung ?
A. 23 B. 24
C. 25 D. Tất cả sai
Câu 5: Cho cấp số cộng (un) có u2 + u3 = 20; u5 + u7 = −29 . Tìm u1 ; d?
A. u1 = 20; d = 7 B. u1 = 20;d = 7
C. u1 = 20,5; d = −7 D. u1 = −20,5; d= 7
Câu 6: Cho cấp số cộng (un) thỏa mãn 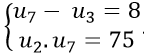
A. u1 = 3; d= 1 B. u1 = 3; d = 2
C. u1 = 2; d = 3 D. u1 = 2; d = −3
Câu 7: Cho cấp số cộng (un) có công sai d > 0 và 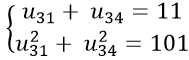
A. un = 3n − 9 B. un = 3n − 42
C. un = 3n − 67 D. un = 3n − 92
Câu 8: Tam giác ABC có ba góc A, B, C theo thứ tự đó lập thành cấp số cộng và C = 5A. Tính tổng số đo của góc có số đo lớn nhất và góc có số đo nhỏ nhất.
A. 1400 B. 1200
C. 1350 D. 1500
Câu 9: Cho (un) là cấp số cộng thỏa mãn : 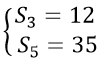
A. 3 B. 4
C. 5 D .6
Câu 10: Cho (un) là cấp số cộng, u1; u2; u3 là 3 số hạng của cấp số cộng thỏa mãn: 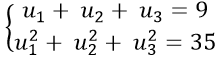
A.15 B. 20
C. 21 D. 18
Câu 11: Cho cấp số cộng (un) có u4 = −20; u19 = 55 . Tìm u1, d của cấp số cộng?
A. u1 = −35; d = 5 B. u1 = −35; d = −5
C. u1 = 35; d = 5 D. u1 = 35; d = −5
Câu 12: Cho (un) là cấp số cộng thỏa mãn : 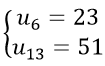
A.6 B.7
C .8 D. 9
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Công thức tính tổng n số hạng đầu của cấp số cộng
Công thức tính công bội của cấp số nhân
Công thức số hạng tổng quát của cấp số nhân
Công thức tính tổng n số hạng đầu của cấp số nhân
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.