Toptailieu.vn giới thiệu Giải bài tập Toán 11 Ôn tập cuối năm hình học chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập ôn tập cuối năm hình học lớp 11.
Giải bài tập Toán 11 Ôn tập cuối năm hình học
Bài tập trang 125, 126 SGK Toán 11
a) Phép tịnh tiến theo vectơ
b) Phép đối xứng qua trục ;
c) Phép đối xứng qua tâm ;
d) Phép quay tâm góc ;
e) Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục và phép vị tự tâm tỉ số .
Phương pháp giải:
a) Sử dụng biểu thức tọa độ của các phép biến hình.
b) Sử dụng biểu thức tọa độ của các phép biến hình.
c) Sử dụng biểu thức tọa độ của các phép biến hình.
d) Sử dụng biểu thức tọa độ của các phép biến hình.
e) Sử dụng biểu thức tọa độ của các phép biến hình.
Lời giải:
a)
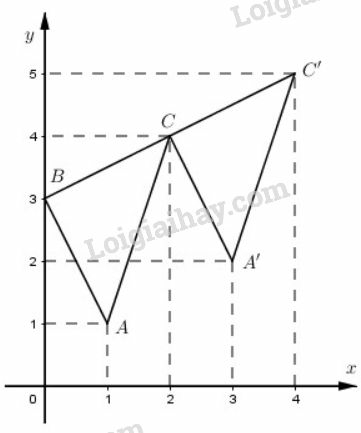
Trong phép tịnh tiến theo vectơ thì các đỉnh có ảnh là các điểm tương ứng .
Từ biểu thức tọa độ
Ta có:
Tam giác , ảnh của tam giác trong phép tịnh tiến theo vectơ là tam giác có ba đỉnh
Dễ thấy đỉnh của trùng với đỉnh của .
b)
Qua phép đối xứng trục , biểu thức tọa độ là :
Do đó ta có: có các đỉnh
c)
Trong phép đối xứng qua tâm , đỉnh thì là trung điểm của . Gọi tọa độ là thì:
Tương tự, ta có ảnh của các đỉnh là
d)
Trong phép quay tâm , góc quay thì tia biến thành tia , tia biến thành tia
Điểm
e)
Trong phép đổi xứng qua . biến thành , ta có:
Với phép vị tự tâm tỉ số thì
Vậy trong phép đồng dạng đã cho thì có ảnh là với .
a) Tìm phép vị tự biến tương ứng thành
b) Chứng minh rằng thẳng hàng.
c) Tìm ảnh của qua phép vị tự
d) Gọi lần lượt là trung điểm của các đoạn thẳng ; theo thứ tự là giao điểm thứ hai của các tia với đường tròn ; tương ứng là chân các đường cao đi qua . Tìm ảnh của , qua phép vị tự tâm tỉ số
e) Chứng minh chín điểm ,,cùng thuộc một đường tròn (đường tròn này gọi là đường tròn Ơ-le của tam giác )
Phương pháp giải:
a) Dựa vào định nghĩa phép vị tự và tính chất trọng tâm của tam giác.
b) Chứng minh hai vectơ cùng phương.
c) Dựa vào định nghĩa phép vị tự.
d) Sử dụng tính chất của phép vị tự: Ảnh của đường tròn qua phép vị tự là 1 đường tròn.
Lời giải:
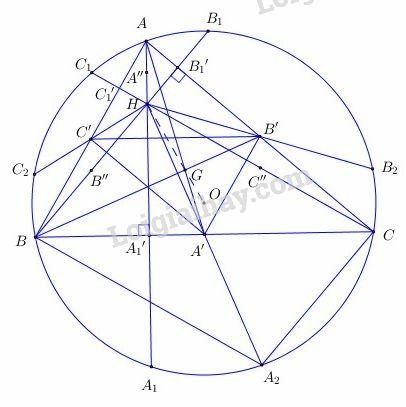
a) Ta có
.
Vậy phép vị tự tâm tỉ số biến thành .
b) là trung điểm của dây nên
Ta lại có . Tương tự
Trong tam giác , nên là trực tâm của .
là trực tâm của và là trực tâm của nên là ảnh của trong phép vị tự tâm , tỉ số
Ba điểm thẳng hàng.
c) Gọi ta có:
Suy ra là trung điểm của đoạn thẳng .
d) Gọi A'', B'', C'' lần lượt là trung điểm của AH, BH, CH ta có:
Vậy là ảnh của các điểm trong phép vị tự .
Ta dễ dàng chứng minh được theo thứ tự là trung điểm của các đoạn thẳng nên:
Như vậy theo thứ tự là ảnh của các điểm trong phép vị tự
e) Gọi theo thứ tự là các điểm xuyên tâm đối của các điểm qua tâm của đường tròn. Ta dễ dàng chứng minh được tứ giác là hình bình hành, do đó và đối xứng qua , ta có:
Như vậy, các điểm theo thứ tự là ảnh của các điểm trong phép vị tự .
Từ đó ta có:
Chín điểm , theo thứ tự là ảnh của các điểm trong phép tự vị mà chín điểm nằm trên đường tròn nên chín điểm nằm trên đường tròn ảnh của đường tròn trong phép vị tự .
a) Chứng minh rằng bốn điểm cùng thuộc một mặt phẳng và mặt phẳng này cắt cả hai mặt phẳng và theo cùng một giao tuyến .
b) Xác định giao tuyến của hai mặt phẳng và .
c) Lấy một điểm trên đoạn và gọi . Chứng minh rằng hai giao điểm của và thuộc đường thẳng nói trên.
Phương pháp giải:
a) Chứng minh mặt phẳng chính là mặt phẳng .
b) Tìm hai điểm chung của hai mặt phẳng và .
c) Gọi , chứng minh là điểm chung của hai mặt phẳng (SAC) và (SBD).
Lời giải:
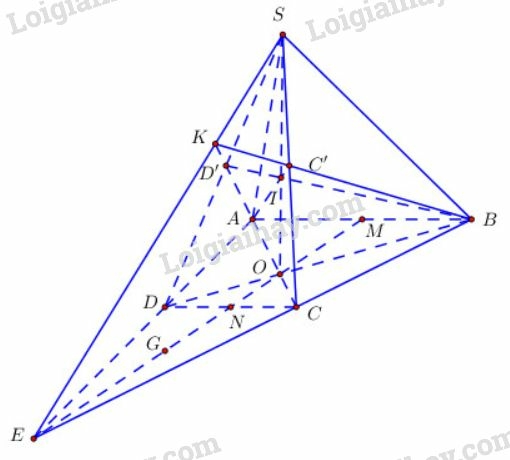
a) Gọi là giao điểm của và ; là giao của và .
là trung điểm của nên là trung điểm của (vì là hình thang)
Mà G là trọng tâm tam giác EDC nên
hay các điểm cùng thuộc mặt phẳng chính là mặt phẳng
Ta dễ thấy
b)
Vậy là một điểm chung của hai mặt phẳng và
là điểm chung của hai mặt phẳng và
c)
Tương tự ta có:
Hai đường thẳng và cùng thuộc mặt phẳng , giả sử
là điểm chung của hai mặt phẳng và hay là giao tuyến của hai mặt phẳng (SAC) và (SBD).
Lời giải:
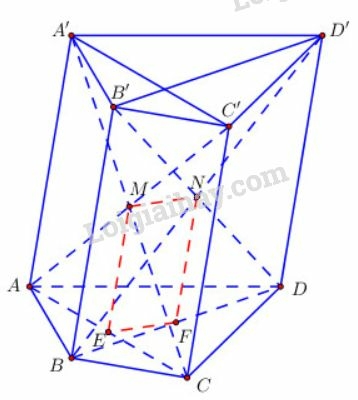
Vì là trung điểm của và là trung điểm của nên là đường trung bình của
Tương tự ta có là đường trung bình của tam giác :
Ta lại có:
Từ (1), (2), (3) ⇒ hay tứ giác là hình bình hành, do đó .
Phương pháp giải:
Xác định giao tuyến của các mặt phẳng đã cho với tất cả các mặt của hình lập phương.
Lời giải:
- Mặt phẳng chính là mặt phẳng , mặt phẳng này chứa cạnh nên
Ta có thiết diện là hình bình hành như hình dưới đây.
Tuy nhiên ta lại có là hình chữ nhật.
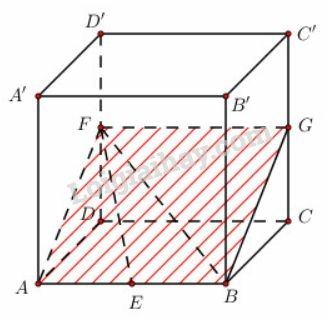
- Trong mặt phẳng tại . Trong mặt phẳng có tại .
Thiết diện cần dựng là hình thang () như hình dưới đây:
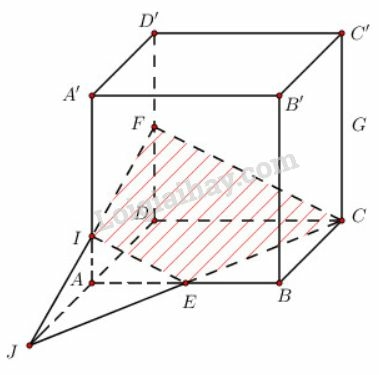
- Trong mặt phẳng , tại . Trong mặt phẳng , tại , là giao tuyến của mặt phẳng với mặt bên .
Trong mặt phẳng , tại . Trong mặt phẳng , tại .
Thiết diện cần dựng là hình ngũ giác như hình dưới đây:
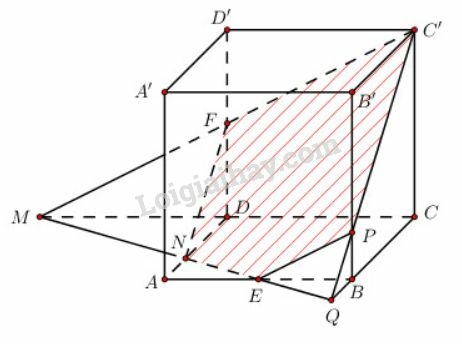
- Gọi theo thứ tự là trung điểm của . Ta dễ dàng chứng minh được 6 điểm nằm trên cùng một mặt phẳng. Mặt phẳng này chính là mặt phẳng và thiết diện có được là hình lục giác . Lục giác này có ba cặp cạnh đối song song và bằng nhau nên nó là lục giác đều. Hình dưới đây:
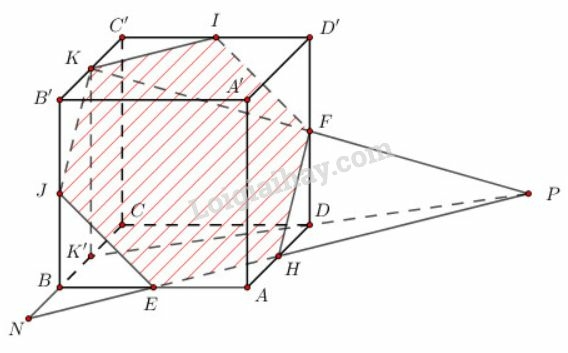
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau và .
b)Tính khoảng cách của hai đường thẳng và .
Lời giải:
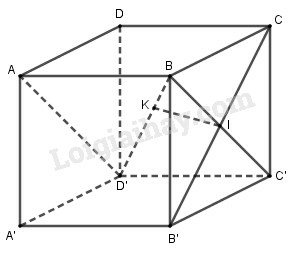
a)
là hình vuông có
Trong mặt phẳng , kẻ .
Vì
Kết hợp với là đường vuông góc chung của và
b) Ta có:
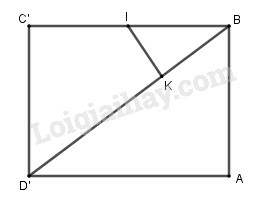
Xét và có:
B chung
Suy ra (g-g)
.
Mà nên:
Vậy .
a)
b) và cùng nằm trên một mặt phẳng.
c) Chứng minh rằng đường thẳng luôn luôn đi qua một điểm cố định khi di động trên tia Ax.
Phương pháp giải:
a) Chứng minh .
b) Chứng minh cả ba đường thẳng cùng vuông góc với , từ đó kết luận chúng cùng thuộc mặt phẳng đi qua A và vuông góc với .
c) Chứng minh ba đường thẳng CD, AB, C'D' đồng quy dựa vào tính chất: Giao tuyến của ba mặt phẳng phân biệt thì đồng quy hoặc đôi một song song.
Lời giải:
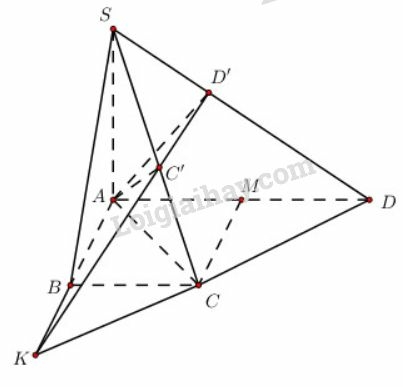
a) Ta có:
(định lí 3 đường vuông góc)
vuông tại .
Gọi là trung điểm của .
Tứ giác có nên là hình bình hành.
Lại có nên là hình vuông
Tam giác có trung tuyến bằng cạnh tương ứng nên nó là tam giác vuông, hay tam giác vuông tại có
(định lí 3 đường vuông góc)
vuông tại .
b) Ta có :
Kết hợp với suy ra
Giả thiết cho (3)
Từ (1), (2), (3) ta thấy ba đường thẳng cùng vuông góc với và chúng cùng đi qua .
Vậy chúng cùng nằm trong mặt phẳng đi qua và vuông góc với .
c) Gọi là giao điểm của với .
là giao điểm của hai mặt phẳng và
Mà .
Vậy ba đường thẳng đồng quy tại và cố định suy ra cố định.
Vậy khi chạy trên thì luôn đi qua điểm cố định là giao điểm của và .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.