Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 1: Hàm số lượng giác chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về hàm số lượng giác lớp 11.
Giải bài tập Toán 11 Bài 1: Hàm số lượng giác
Trả lời câu hỏi giữa bài:
b) Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bằng x (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lấy π ≈ 3,14)
Phương pháp giải:
Nhập các giá trị tương ứng vào hàm sin, cos trên máy tính bỏ túi
Lời giải:
a)
b)
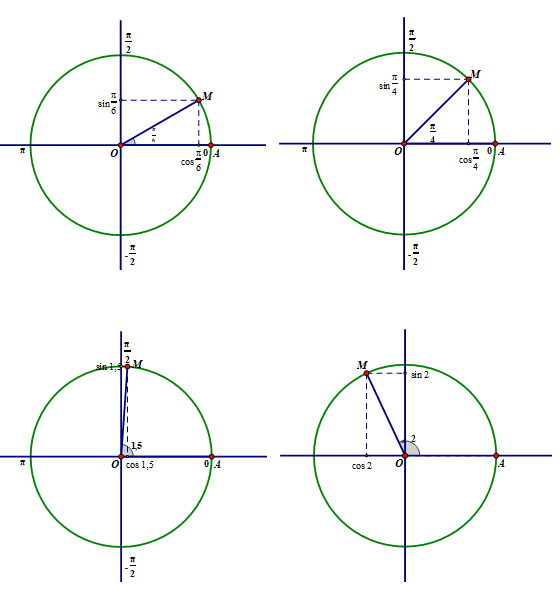
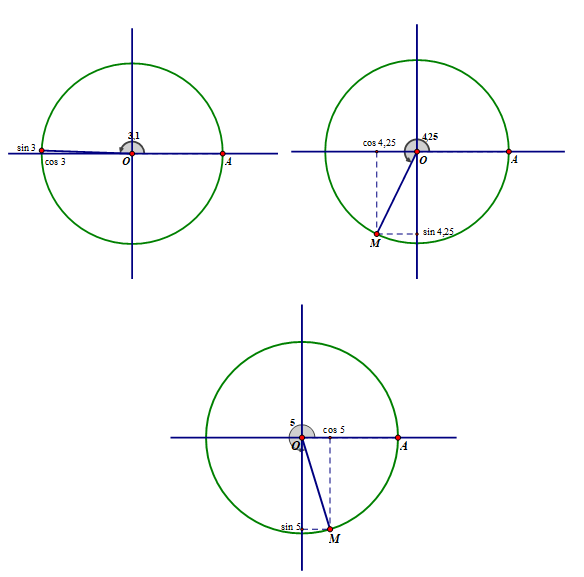
B1: Vẽ hai góc và trên đường tròn lượng giác.
B2: xác định và trên đường tròn lượng giác
B3: so sánh và rút ra KL.
Lời giải:
a) ;
b) .
Phương pháp giải:
a) Sử dụng công thức .
b) Sử dụng công thức để chỉ ra T .
Lời giải:
a)
vì .
b)
vì .
Bài tập trang 17, 18 SGK Toán 11
a) Nhận giá trị bằng ;
b) Nhận giá trị bằng ;
c) Nhận giá trị dương;
d) Nhận giá trị âm.
Phương pháp giải:
a)
B1: Vẽ đường thẳng y=0 (Ox)
B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=0 tại những điểm nào.
B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.
b)
B1: Vẽ đường thẳng y=1 (Ox)
B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=1 tại những điểm nào.
B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.
c)
B1: Quan sát đồ thị hàm số, tìm các giá trị x sao cho đồ thị nằm phía trên trục hoành (hay tanx >0).
B2. Lấy các điểm thuộc đoạn đề bài yêu cầu và Kết luận.
d)
Quan sát đồ thị hàm số, tìm các điểm thỏa mãn yêu cầu bài toán.
Lời giải:
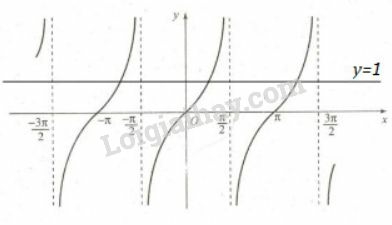
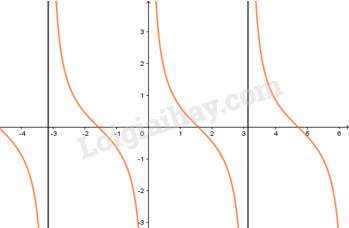
Trong đoạn ,
Trục hoành cắt đồ thị hàm số tại ba điểm có hoành độ .
Vậy .
b)
Đường thẳng cắt đồ thị tại ba điểm có hoành độ .
Vậy .
c)
Trong các khoảng ; ; , đồ thị hàm số nằm phía trên trục hoành.
Vậy .
d)
Trong các khoảng , đồ thị hàm số nằm phía dưới trục hoành.
Vậy .
b) ;
c) ;
d) .
Phương pháp giải:
a) Hàm số có dạng xác định khi và chỉ khi .
b) Hàm số có dạng xác định khi và chỉ khi .
c) Hàm số xác định khi và chỉ khi .
d) Hàm số xác định khi và chỉ khi .
Lời giải:
a)
Hàm số xác định khi
Vậy tập xác định của hàm số là
b)
Hàm số xác định khi:
Vì và
Do đó với mọi thỏa mãn
Vậy tập xác định của hàm số là
c)
Hàm số xác định khi
Vậy tập xác định của hàm số
d)
Hàm số xác định khi
Vậy tập xác định của hàm số là
Phương pháp giải:
Phương pháp vẽ đồ thị hàm số
Bước 1: Vẽ đồ thị hàm số .
Bước 2: Lấy đối xứng phần đồ thị phía dưới trục hoành của hàm số qua trục Ox.
Bước 3: Xóa đi phần đồ thị phía dưới trục hoành của hàm số .
Lời giải:
Ta có
Bước 1: Vẽ đồ thị hàm số .
Bước 2: Lấy đối xứng phần đồ thị phía dưới trục hoành của hàm số qua trục Ox.
Bước 3: Xóa đi phần đồ thị phía dưới trục hoành của hàm số .
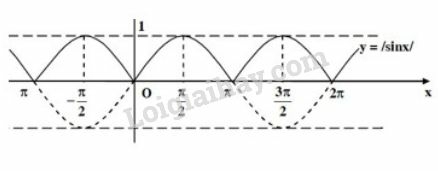
Khi đó ta được đồ thị hàm số như sau:
Phương pháp giải:
Dựa vào tính tuần hoàn và chu kì của hàm số : Hàm là hàm tuần hoàn với chu kì .
Lời giải:
Hàm là hàm tuần hoàn với chu kì nên ta có:
Ta có:
Hàm số tuần là hàm tuần hoàn với chu kì .
Xét hàm số trên đoạn .
Ta lấy các điểm đặc biệt như sau:

Từ đó ta có đồ thị hàm số trên đoạn là:
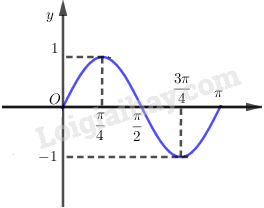
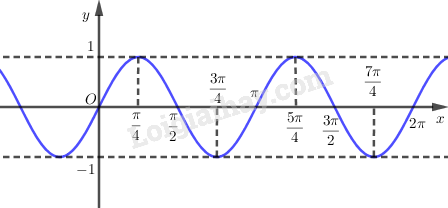
Do hàm số tuần hoàn với chu kì nên ta có đồ thị là:
Phương pháp giải:
B1: Vẽ đường thẳng ( song song và ở trên trục hoành, cách trục hoành một khoảng là 1/2)
B2: xác định các điểm cắt của d và đồ thị, dự đoán giá trị của x.
B3. Dựa vào tính tuần hoàn để KL nghiệm.
Lời giải:
Nghiệm của phương trình là các hoành độ giao điểm của đường thẳng và đồ thị .
Trong đó đường thẳng là đường thẳng song song với trục hoành, đi qua điểm , còn hàm số có đồ thị như hình dưới
Cách 1:
Ta xác định các giao điểm, lấy hoành độ (tức là gióng xuống trục Ox)
Suy ra .
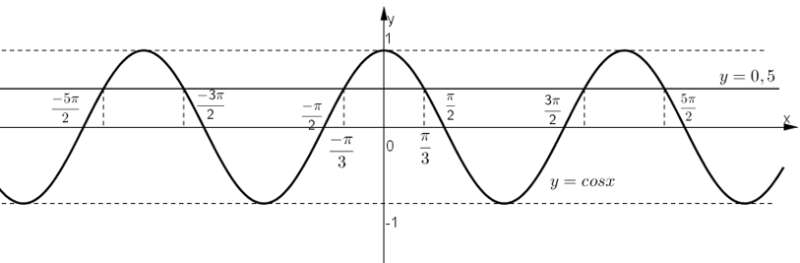
Cách 2: Xét trong đoạn và sử dụng tính tuần hoàn để suy ra tất cả các giá trị của
Dễ thấy: trong đoạn này chỉ có giao điểm ứng với thỏa mãn
Suy ra các giá trị của là .
Phương pháp giải:
B1: Tìm các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía trên trục hoành trong khoảng
B2: dựa vào chu kì tuần hoàn của hàm số suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía trên trục hoành.
Lời giải:
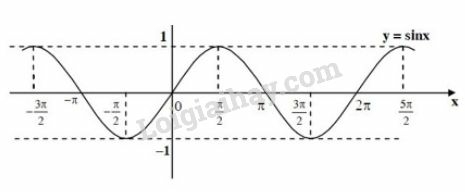
Nhìn đồ thị ta thấy trong đoạn các điểm nằm phía trên trục hoành của đồ thị là các điểm có hoành độ thuộc khoảng .
Hàm số là hàm số tuần hoàn với chu kì . Từ đó, tất cả các khoảng giá trị của để hàm số đó nhận giá trị dương là hay với .
B1: Tìm các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía dưới trục hoành trong khoảng
B2: Dựa vào chu kì tuần hoàn của đồ thị hàm số suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía dưới trục hoành.
Lời giải:
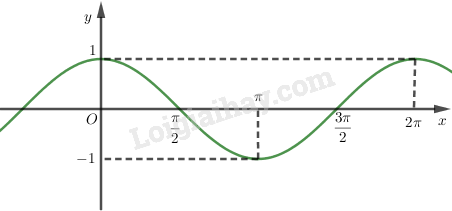
Xét trên đoạn , dựa vào đồ thị hàm số , để làm hàm số nhận giá trị âm thì:
Do hàm số tuần hoàn với chu kì nên tất cả các khoảng mà đồ thị hàm số nằm phía dưới trục hoành là .
a) ;
b) .
Phương pháp giải:
a) Sử dụng tập giá trị của hàm sin và cos: .
b) Sử dụng tập giá trị của hàm sin và cos: .
Lời giải:
a)
Điều kiện: .
Vì nên kết hợp điều kiện ta có
.
Do dó khi .
b)
ta có: .
Vậy khi .
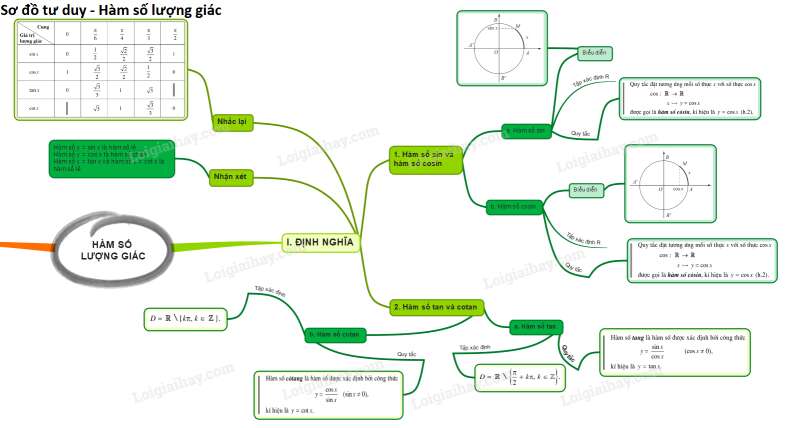
Lý thuyết Bài 1: Hàm số lượng giác
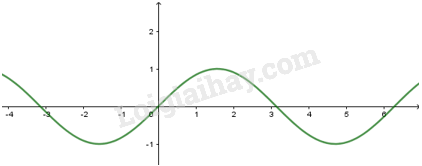
1. Hàm số
- Có TXĐ , là hàm số lẻ, tuần hoàn với chu kì , nhận mọi giá trị thuộc đoạn .
- Đồng biến trên mỗi khoảng và nghịch biến trên mỗi khoảng
- Có đồ thị là đường hình sin đi qua điểm
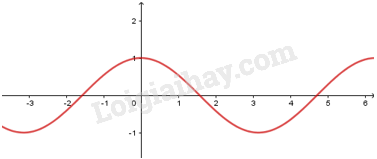
2. Hàm số
- Có TXĐ , là hàm số chẵn, tuần hoàn với chu kì , nhận mọi giá trị thuộc đoạn .
- Đồng biến trên mỗi khoảng và nghịch biến trên mỗi khoảng
- Có đồ thị là đường hình sin đi qua điểm
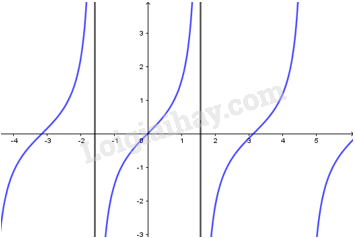
3. Hàm số
- Có TXĐ , là hàm số lẻ, tuần hoàn với chu kì , nhận mọi giá trị thuộc .
- Đồng biến trên mỗi khoảng .
4. Hàm số
- Có TXĐ , là hàm số lẻ, tuần hoàn với chu kì , nhận mọi giá trị thuộc .
- Nghịch biến trên mỗi khoảng .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.