Toptailieu.vn xin giới thiệu 35 câu trắc nghiệm Hàm số lượng giác (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

35 câu trắc nghiệm Hàm số lượng giác (có đáp án) chọn lọc

Câu 1. Hàm số y = cosx/(2sinx- √3) có tập xác định là:

A. R\{π/3+k2π, k ∈ Z}.                             

B. R\{π/6+kπ, k ∈ Z}.

C. R\{π/6+k2π, 5π/6+k2π, k ∈ Z}.        

   D. R\{π/3+k2π, 2π/3+k2π, k ∈ Z}.

Lời giải:

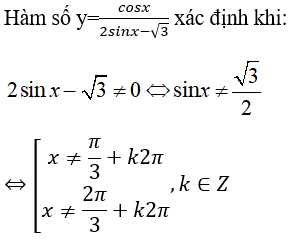
Chọn đáp án D

Câu 2. Hàm số y = tan(x/2 - π/4) có tập xác định là:

A. R\{π/2+k2π, k ∈ Z}.                  

  B. R\{π/2+kπ, k ∈ Z}.

C. R\{3π/2+k2π, k ∈ Z}.                 

D. R.

Lời giải:

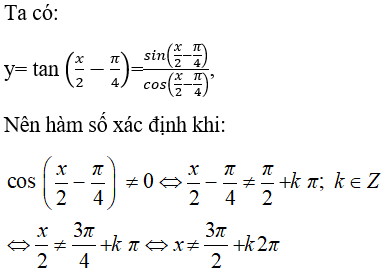
Chọn đáp án C

Câu 3. Tập xác định của hàm số y = cot(2x - π/3) + 2 là:

A. R\{π/6+kπ, k ∈ Z}.                   

   B. R\{π/6+k2π, k ∈ Z}.

C. R\{5π/12+kπ/2, k ∈ Z}.             

D. R\{π/6+kπ/2, k ∈ Z}.

Lời giải:

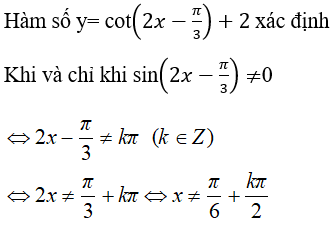
Chọn đáp án D

Câu 4. Hàm số : 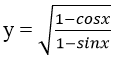có tập xác định là:

A. R\{kπ, k ∈ Z}.                           

    B. R\{π/2+π, k ∈ Z}.

C. R\{π/2+k2π, k ∈ Z}.                 

   D. R\{kπ/2, k ∈ Z}.

Lời giải:

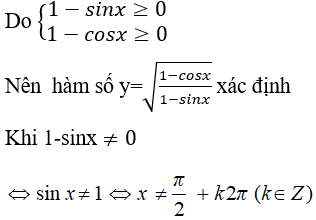
Chọn đáp án C

Câu 5. Cho hàm số y = sinx/(1+tanx) và k ∈ Z.

Khoảng nào dưới đây không nằm trong tập xác định của hàm số?

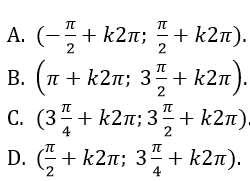
Lời giải:

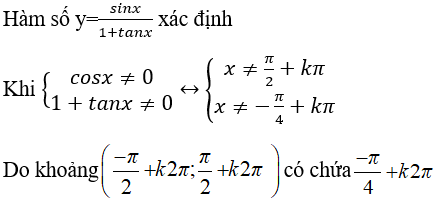
Nên khoảng này không nằm trong tập xác định của hàm số

Chọn đáp án A

Câu 6. Hàm số : 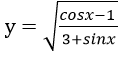có tập xác định là:

A. R                                                 

B. R\{k2π, k ∈ Z}.

C. {k2π, k ∈ Z}.                               

D. ∅.

Lời giải:

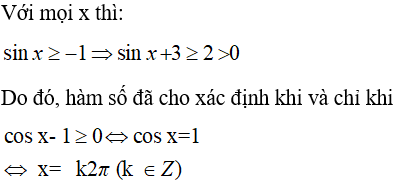
Chọn đáp án C

Câu 7. Hàm số y = sinxcos2x là:

A. Hàm chẵn.                                                 

B. Hàm không có tính chẵn, lẻ.

C. Hàm không có tính tuần hoàn.                   

D. Hàm lẻ.

Lời giải:

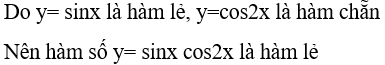
Chọn đáp án D

Câu 8. Hàm số 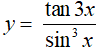 thỏa mãn tính chất nào sau đây?

A. Hàm chẵn.                                

B. Hàm không có tính chẵn, lẻ.

C. Xác định trên R.                        

D. Hàm lẻ.

Lời giải:

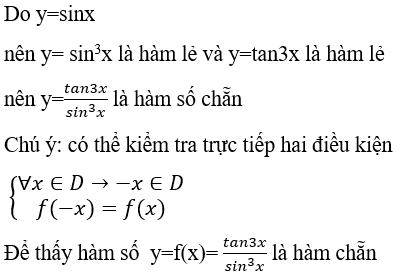
Chọn đáp án A

Câu 9. Trong các hàm số sau, hàm số nào là hàm lẻ?

A. y = sin²x                                  

B. y = sin²x.cosx.

C. y = tanx/cosx.                           

D. y = cotx/sinx.

Lời giải:

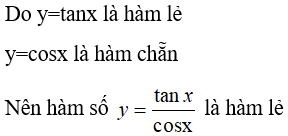
Chọn đáp án C

Câu 10. Trong các hàm số sau, hàm số nào là hàm chẵn?

A.                            

B. y = sinx.cos2x

C. y = cosx.sin²x                                   

D. y = cosxsin³x.

Lời giải:

Do y = sin²x và y = cosx là hàm chẵn nên hàm số y = cosx. sin²x là hàm chẵn.

Chọn đáp án C

Câu 11: Trong các hàm số sau, hàm số nào không là hàm chẵn và cũng không là hàm lẻ?

A. y = tanx - 1/sinx.                     

B. y = √2 sin(x - π/4).

C. y = sinx + tanx.                        

D. y = sin⁴x – cos⁴x.

Lời giải:

Xét phương án B:

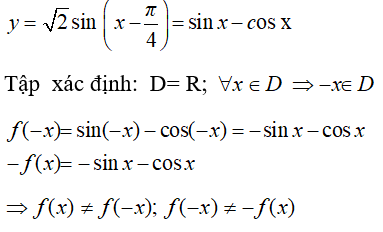
Do đó, hàm số đã cho không là hàm chẵn và cũng không phải là hàm lẻ

Chọn đáp án B

Câu 12: Hàm số y = (sinx + cosx)² + cos2x có giá trị lớn nhất là:

A. 1+√2      

B. 3

C. 5            

D. √2

Lời giải:

Ta có:

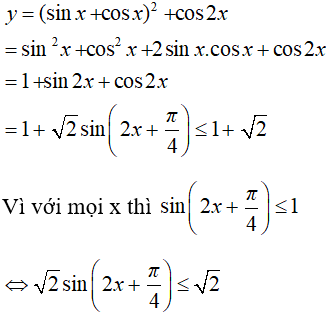
Suy ra hàm số có giá trị lớn nhất là 1 + √2

Chọn đáp án A

Câu 13: Hàm số y = √3sinx – cosx có giá trị nhỏ nhất là:

A. 1 – √3      

B. - √3

C. – 2            

D. – 1 – √3

Lời giải:

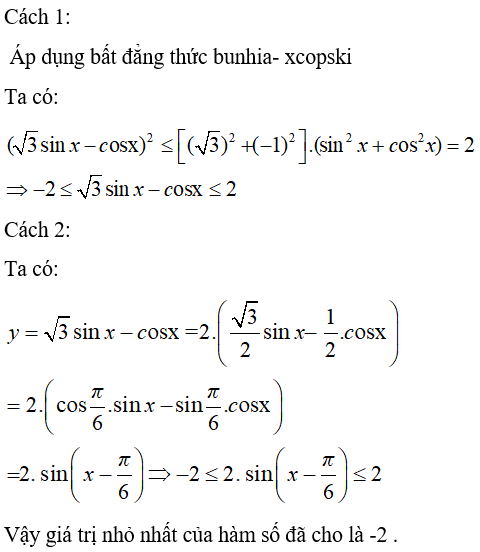
Chọn đáp án C

Câu 14: Cho hàm số y = (cosx-1)/(cosx+2). Mệnh đề nào trong số các mệnh đề sau đây là sai?

A. Tập xác định của hàm số là ℝ.                            

B. Hàm số có giá trị lớn nhất bằng 0.

C. Hàm số có giá trị nhỏ nhất bằng - 2.                 

D. Hàm số tuần hoàn với chu kì T = 2.

Lời giải:

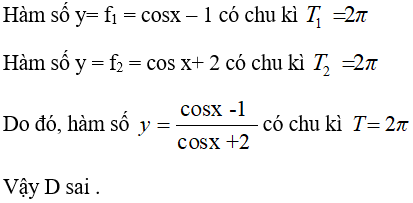
Chọn đáp án D

Câu 15: Hàm số nào sau đây có giá trị lớn nhất bằng 2?

A. y = tanx – cotx                          

B. y = 2tanx

C. y = √2(cosx – sinx)                   

D. y = sin(2x - π/4)

Lời giải:

Các hàm số y= tanx- cotx và y= 2tanx không có giá trị lớn nhất, hàm số y= sin(2x-π/4) có giá trị lớn nhất là 1

Cũng có thể nhận ngay ra đáp án C vì:

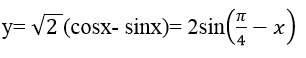
Chọn đáp án C

Câu 16: Giá trị nhỏ nhất của hàm số y = 3- 4sin²xcos²x là:

A. – 1      

B. 2

C. 1         

D. 3

Lời giải:

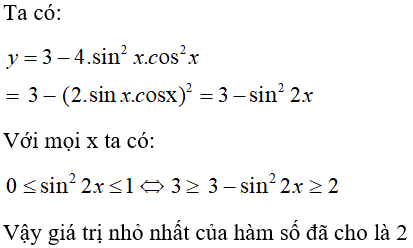
Chọn đáp án B

Câu 17: Hàm số y = √(1-cos2x) có chu kì là:

A. 2π      

B. √2π

C. π         

D. √π

Lời giải:

Tập xác định của hàm số đã cho là R mà cos2x có chu kì là π nên y= √(1-cos2x) cũng có chu kì là π

Chọn đáp án C

Câu 18:Hai hàm số nào sau đây có chu kì khác nhau?

A. cos(x/2) và sin(x/2).             

B. Sinx và tanx.

C. cosx và cot(x/2).                 

D. tan2x và cot2x.

Lời giải:

Hàm số sinx có chu kì là 2π, hàm số tanx có chu kì là π

Vậy hai hàm số y = sinx và y = tan x có chu kì khác nhau.

Chọn đáp án B

Câu 19: Chu kì của hàm số y = 2sin(2x + π/3) -3cos(2x - π/4) là:

A. 2π       B. π

C. π/2      D. 4 π

Lời giải:

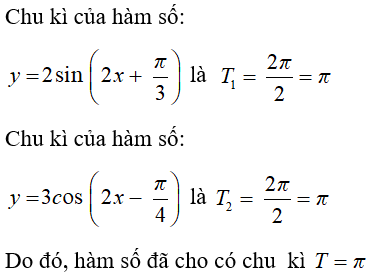
Chọn đáp án B

Câu 20: Chu kì của hàm số y = sin2x -2cos3x là:

A. 2π             

B. π

C. (2π)/3      

D. π/3

Lời giải:

Chu kì của hàm số y=sin2x là π, chu kì của hàm số y=cos3x là (2π)/3 nên chu kì của hàm số đã cho là 2π

Chọn đáp án A

Câu 21: Hàm số nào sau đây không phải làm hàm số lẻ?

A. y = sinx                            

B. y = cosx

C. y = tanx                          

D. y = cotx

Lời giải:

Do cos ( -x) = cosx với mọi x ∈ R nên y = cosx không là hàm lẻ.

Chọn đáp án là B.

Câu 22: Hàm số y =sinxcosx là:

A. Hàm không có tính chẵn, lẻ                        

B. Hàm chẵn

C. Hàm có giá trị lớn nhất bằng 1                   

D. Hàm lẻ.

Lời giải:

Kí hiệu f(x) = sinxcosx. Hàm số có tập xác định D = R.

∀x ∈ D thì –x ∈ D và f( -x) = sin(-x)cos(-x) = - sinxcosx = - f(x).

Vậy y = sinxcosx là hàm số lẻ.

Chọn đáp án là D

Câu 23: Hàm số y = 2sinxcosx + cos2x có giá trị lớn nhất là

A. 3                  

B. 2√2

C. 2                  

D. √2

Lời giải:

Ta có

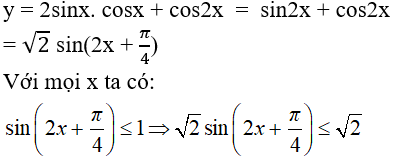
Vậy giá trị lớn nhất của hàm số là √2.

Đáp án là D.

Câu 24: Hàm số y = (sinx – cosx)² + cos2x có giá trị nhỏ nhất là:

A. – 1        

B. 1 - √2

C. 0           

D. 1 + √2

Lời giải:

Ta có y = sin²x + cos²x -2sinxcosx + cos2x

= 1 – sin2x + cos2x = 1 - √2 sin(2x - π/4).

Với mọi x ta có:

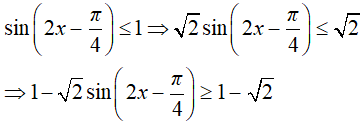
Từ đó suy ra giá trị nhỏ nhất của hàm số là 1 - √2.

Đáp án là B.

Câu 25: Tìm tập xác định D của hàm số y = (sinx + 2)/ (sinx.cos2x)

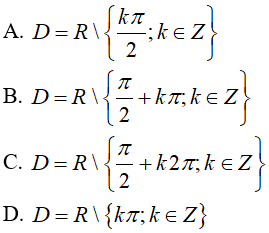
Hiển thị đáp án

Hàm số xác định khi

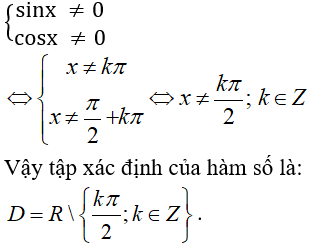
Vậy tập xác định của hàm số là D = R\ {kπ/2, k ∈ Z}.

Đáp án là A.

Câu 26: Tập xác định D của hàm số y = √((2cosx+3)/(sinx+1)) là:

A. D = R\ {-π/2+kπ, k ∈ Z}                       

B. D = R\ {-π/2+k2π, k ∈ Z}

C. D = R                                                   

D. D = R\ {π/2+k2π, k ∈ Z}

Lời giải:

Hàm số xác định khi

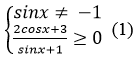
Do – 1 ≤sinx ≤1, – 1 ≤cosx ≤1 nên 2cosx + 3 > 0 và sinx + 1 ≥0, ∀x ∈ R.

Từ đó suy ra (1) ⇔ sinx ≠ -1 ⇔ x ≠ - π/2+k2π.

Vậy tập xác định của hàm số là D = R\ {-π/2+k2π, k ∈ Z}.

Đáp án là B.

Câu 27: Hàm số y = 2cos²x – 1 là hàm tuần hoàn với chu kì:

A. T = π.            

B. T = 2π.

C. T = π2.          

D. T = π/2.

Lời giải:

Ta có y = 2cos²x – 1 = cos2x, do đó hàm số tuần hoàn với chu kì T = 2π/2 = π.

Vậy đáp án là A.

Câu 28: Hàm số y = sin(π/2-x) + cotx/3 là hàm tuần hoàn với chu kì:

A. T = π.                      

B. T = 2π.

C. T = 3π.                    

D. T = 6π.

Lời giải:

Hàm số y₁ = sin(π/2-x) có chu kì T₁ = 2π/|-1| = 2π;

Hàm số y₂ = cot(x/3) có chu kì T₂ = 2π/|1/3| = 3 π. Suy ra hàm số đã cho y = y₁ +y₂ có chu kì T =BCNN(2,3).π = 6π.

Vậy đáp án là D.

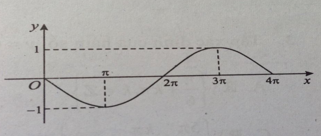
Câu 29: Hình vẽ bên là một phần đồ thị của hàm số nào sau đây?

A. y = sinx/2                           

B. y = cosx/2

C. y = - cosx/4                       

D. y = sin( - x/2)

Lời giải:

Đồ thị hàm số đi qua gốc tọa độ nên loại ngay các phương án B và C. Đồ thị hàm số đi qua (π; -1) nên phương án A cũng không thỏa mãn.

Nhận xét: Từ đồ thị ta nhận thấy hàm số có chu kì T =4π nên ta có thể loại ngay phương án C.

Vậy đáp án là D.

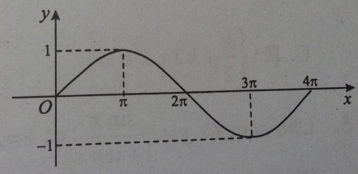
Câu 30: Hình vẽ bên là một phần đồ thị của hàm số nào sau đây?

A. y = sinx/2                           

B. y = sinx

C. y = cosx/2                         

D. y = cosx

Lời giải:

Từ đồ thị ta nhận thấy hàm số có chu kì T =4π nên ta có thể loại ngay phương án B và D. Do đồ thị hàm số đi qua gốc tọa độ nên ta loại tiếp phương án C.

Vậy đáp án là A.

Câu 31: Hàm số y = 2sinxcosx + cos2xy = 2sinxcosx + cos2x có giá trị lớn nhất là

A. 3                               

B. 2√2

C. 2                              

D. √2

Lời giải:

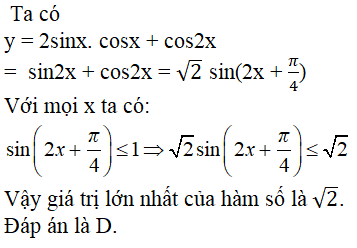
Câu 32: Hàm số y = tan(x/2 − π/4) y = tan(x/2 - π/4) có tập xác định là:

A. R\{π/2+k2π, k ∈ Z}.                    

B. R\{π/2+kπ, k ∈ Z}.

C. R\{3π/2+k2π, k ∈ Z}.                 

D. R.

Lời giải:

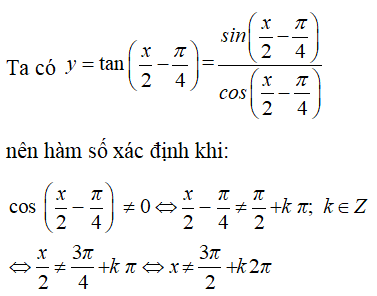
Chọn C.

Câu 33: Trong các hàm số sau, hàm số nào là hàm lẻ?

A. y = sin2xy = sin2x            

B. y = sin2x.cosx.y = sin2x.cosx.

C. y = tanx/cosx.                  

D. y = cotx/sinx.

Lời giải:

Xét phương án C: 

Cách 1:

Do y=tanx là hàm lẻ, y=cosx là hàm chẵn nên hàm số y =  tanxcosxy =  tanxcosx là hàm số lẻ

Cách 2

Đặt y= f(x) =  tanxcosxy= f(x) =  tanxcosx

f(−x) =  tan(−x)cos(−x)= − tan xcosx f(-x) =  tan(-x)cos(-x)= - tan xcosx 

suy ra: f(-x) = - f(x) nên hàm số này là hàm số lẻ

Chọn C.

Câu 34: Hàm số y =sinx.cosx là

A. Hàm không có tính chẵn, lẻ               

B. Hàm chẵn

C. Hàm có giá trị lớn nhất bằng 1             

D. Hàm lẻ.

Lời giải:

Kí hiệu f (x) = sinxcosx. Hàm số có tập xác định D = ℝ.

∀x∈D thì −x∈D∀x∈D thì -x∈Dvà f(-x) = sin(-x)cos(-x) = - sinx.cosx = - f(x).

Vậy y = sinxcosx là hàm số lẻ.

Đáp án là D.

Câu 34: Hàm số y = tan(x/2 − π/4) y = tan(x/2 - π/4) có tập xác định là:

A. R\{π/2+k2π, k ∈ Z}.                    

B. R\{π/2+kπ, k ∈ Z}.

C. R\{3π/2+k2π, k ∈ Z}.                 

D. R.

Lời giải:

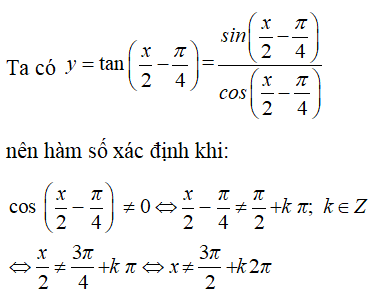
Chọn C

Câu 35: Hàm số y=(sinx+cosx)2 + cos2xy=(sinx+cosx)2 + cos2x có giá trị lớn nhất là:

A. 1+√1+2                    

B. 3

C. 5                              

D. √2

Lời giải:

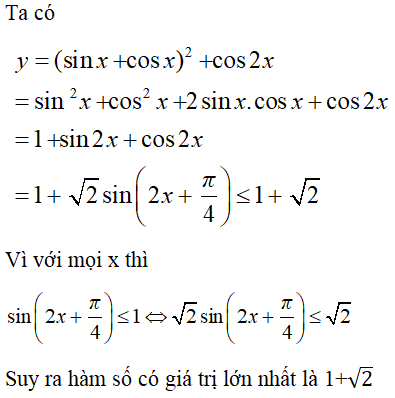
Chọn A.