Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 12.

SBT Toán 11 (Kết nối tri thức) Bài 12: Đường thẳng và mặt phẳng song song

Bài 4.22 trang 63 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng

a) CD//(ABEF) 

b) EF//(ABCD)   

c) CE//(ADF)

(Gợi ý: Theo SGK Bài 11, Luyện tập 3, ta đã biết CEFD là hình bình hành)

Lời giải:

a) Vì ABCD là hình bình hành nên AB//CD, mà $AB\subset \left(ABEF\right)$ nên CD//(ABEF)

b) Vì ABEF là hình bình hành nên EF//AB, mà $AB\subset \left(ABCD\right)$ nên EF//(ABCD)

c) Vì CEFD là hình bình hành nên CE//DF, mà $DF\subset \left(ADF\right)$ nên CE//(ADF)

Bài 4.23 trang 63 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi K và L lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng:

a) KL//(ADF)                

b) KL//(BCE)

Lời giải:

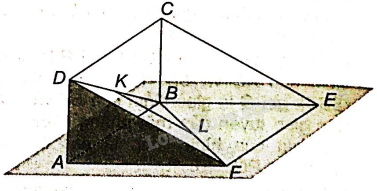
a) KL là đường trung bình của tam giác BDF nên KL//DF, mà $DF\subset \left(ADF\right)$ nên KL//(ADF)

b) Vì KL là đường trung bình của tam giác ACE nên KL//CE, mà $CE\subset \left(CBE\right)$ nên KL//(BCE)

Bài 4.24 trang 63 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G và H lần lượt là trọng tâm của hai tam giác ABC và ACD. Chứng minh rằng GH//(BCD)

Lời giải:

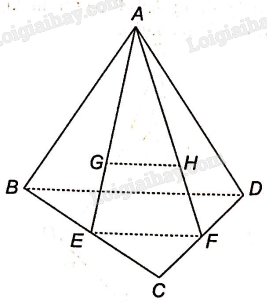
Gọi E, F lần lượt là trung điểm của các cạnh BC, CD. Vì G là trọng tâm của tam giác ABC nên A, G, E thẳng hàng và $\frac{AG}{AE}=\frac{2}{3}$

Tương tự ta có A, H, F thẳng hàng và $\frac{AH}{AF}=\frac{2}{3}.$

Do đó, $\frac{AG}{AE}=\frac{AH}{AF}$

Trong tam giác AEF có: $\frac{AG}{AE}=\frac{AH}{AF}$, theo định lí Thalès đảo ta có GH//EF, mà $EF\subset \left(BCD\right)$ nên GH//(BCD) 

Bài 4.25 trang 63 SBT Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD và E là một điểm bất kì thuộc cạnh SA. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng SB, SD. Gọi M, N lần lượt là giao điểm của (P) và các cạnh AB, AD.

a) Chứng minh rằng EM//SB và EN//SD.

b) Giả sử đường thẳng MN cắt các đường thẳng BC, CD. Xác định giao tuyến của mặt phẳng (P) và các mặt phẳng (SBC), (SCD).

Lời giải:

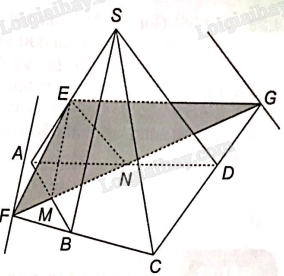
a) Mặt phẳng (SAB) chứa đường thẳng SB song song với mặt phẳng (P) nên giao tuyến của hai mặt phẳng đó song song với SB, suy ra EM//SB.

Mặt phẳng (SAD) có đường thẳng SD song song với mặt phẳng (P) nên giao tuyến của hai mặt phẳng đó song song với SD, suy ra EN//SD

b) Gọi F, G lần lượt là giao điểm của đường thẳng MN và hai đường thẳng BC, CD. Trong mặt phẳng (SBC), vẽ đường thẳng qua F song song với SB thì đường thẳng đó là giao tuyến của mặt phẳng (P) và mặt phẳng (SBC).

Trong mặt phẳng (SCD), vẽ đường thẳng qua G và song song với SD thì đường thẳng đó là giao tuyến của mặt phẳng (P) và mặt phẳng (SCD).

Bài 4.26 trang 63 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm bất kì thuộc cạnh SA. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB và SC.

a) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (SAC), từ đó tìm một điểm chung của mặt phẳng (P) và mặt phẳng (ABCD).

b) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (ABCD).

c) Xác định giao tuyến của mặt phẳng (P) và các mặt còn lại của hình chóp.

Lời giải:

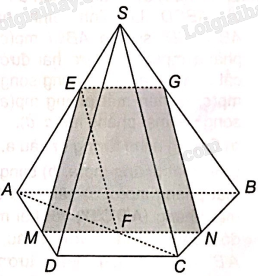
a) Mặt phẳng (SAC) chứa đường thẳng SC song song với mặt phẳng (P) nên giao tuyến của hai mặt phẳng (SAC) và (P) song song với SC. Do đó, trong mặt phẳng (SAC), vẽ đường thẳng EF//SC (F thuộc AC) thì EF là giao tuyến của hai mặt phẳng (P) và (SAC). Điểm F là điểm chung của mặt phẳng (P) và mặt phẳng (ABCD).

b) Trong mặt phẳng (ABCD), vẽ đường thẳng MN qua F song song với AB $\left(M\in AD,N\in BC\right)$ thì MN là giao tuyến của (P) và mặt phẳng (ABCD)

c) Trong mặt phẳng (SAB), vẽ đường thẳng EG//AB (G thuộc SB) thì EG là giao tuyến của hai mặt phẳng (P) và (SAB). Các giao tuyến của (P) và các mặt của hình chóp là EG, MN, EM, GN.

Bài 4.27 trang 63 SBT Toán 11 Tập 1: Một tấm bảng hình chữ nhật được đặt dựa vào tường như trong Hình 4.18. Hãy giải thích vì sao mép trên của tấm bảng song song với mặt đất, mép dưới của tấm bảng song song với mặt tường.

Lời giải:

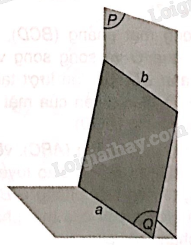
Gọi (P) là mặt tường và (Q) là mặt bảng. Gọi a là mép dưới của bảng và b là mép trên thì b nằm trong (P). Vì bảng có dạng hình chữ nhật nên a//b, do đó a//(P), tức là mép dưới của bảng song song với mặt tường.

Tương tự ta có mép trên của bảng song song với mặt đất.

Bài 4.28 trang 63 SBT Toán 11 Tập 1: Để dựng dây phơi quần áo, bác Việt lắp hai thanh sắt đứng có chiều dài bằng nhau trên mặt đất và căng dây nối hai đầu còn lại của hai thanh sắt (H.4.19). Khi đó, dây phơi có song song với mặt đất không? Giải thích vì sao.

Lời giải:

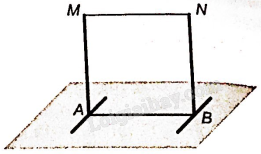
Gọi hai đầu của hai thanh sắt trên mặt đất A, B và hai đầu tương ứng còn lại là M, N thì AM//BN và $AM=BN,$ suy ra ABNM là hình bình hành. Vì vậy MN//AB và do đó dây phơi (nối hai điểm M, N) song song với mặt đất (chứa đường thẳng AB).

Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 11: Hai đường thẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4 trang 72

Bài 15: Giới hạn của dãy số