Toptailieu.vn biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 10.

SBT Toán 11 (Kết nối tri thức) Bài 10: Đường thẳng và mặt phẳng trong không gian

SBT Toán 11 trang 55 Tập 1 (Kết nối tri thức)

Bài 4.1 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Gọi M là một điểm bất kì thuộc cạnh SC.

a) Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD).

b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD).

Lời giải:

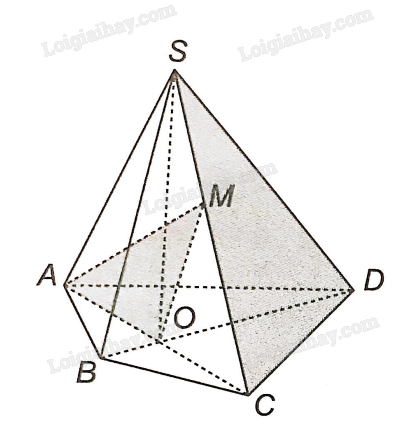
a) Ta thấy M thuộc AM, nằm trong mặt phẳng (AMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (AMO) và (SCD).

Ta thấy C thuộc đường thẳng AC (trùng với đường thẳng AO nên nó nằm trong mặt phẳng (AMO). C lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy C là điểm chung thứ hai của (AMO) và (SCD).

Vậy nên MC (hay SC) là giao tuyến của hai mặt phẳng (AMO) và (SCD).

b) Ta thấy M thuộc BM, nằm trong mặt phẳng (BMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (BMO) và (SCD).

Ta thấy D thuộc đường thẳng BD (trùng với đường thẳng BO nên nó nằm trong mặt phẳng (BMO). D lại thuộc SD, nằm trong mặt phẳng (SCD). Vậy D là điểm chung thứ hai của (BMO) và (SCD).

Vậy nên MD là giao tuyến của hai mặt phẳng (BMO) và (SCD).

Bài 4.2 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD.

a) Xác định giao tuyến của hai mặt phẳng (SAM) và (SCD).

b) Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD).

c) Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN).

Lời giải:

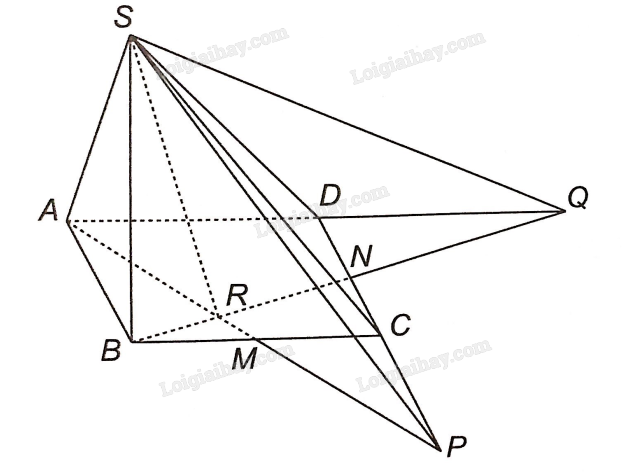
a) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SCD).

Trong mặt phẳng (ABCD): Gọi P là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SAM) và (SCD).

Vậy SP là giao tuyến của (SAM) và (SCD).

b) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SBN) và (SAD).

Trong mặt phẳng (ABCD): Gọi Q là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng  (SBN) và (SAD).

Vậy SQ là giao tuyến của  (SBN) và (SAD).

c) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SBN).

Trong mặt phẳng (ABCD): Gọi R là giao điểm của AM và BN => R là điểm chung thứ hai của mặt phẳng  (SAM) và (SBN).

Vậy SR là giao tuyến của  (SAM) và (SBN).

Bài 4.3 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Gọi P là điểm thuộc cạnh AD sao cho AP = 2 DP. Xác định giao tuyến của hai mặt phẳng (MNP) và (BCD).

Lời giải:

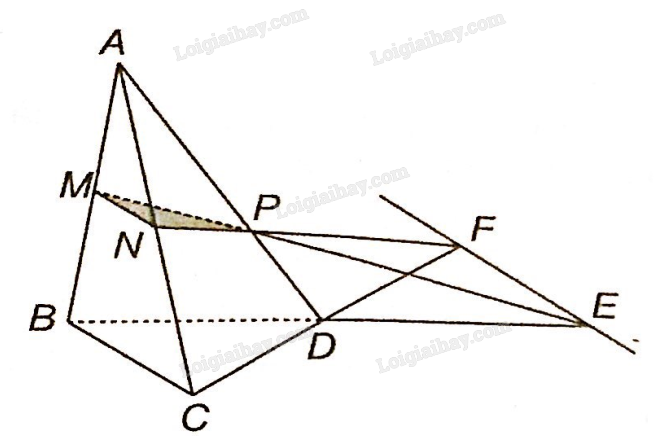
Trên mặt phẳng (ABD): gọi giao điểm của MP và BD là E. Vậy E là điểm chung thứ nhất của hai mặt phẳng (MNP) và (BCD)

Trên mặt phẳng (ACD): gọi giao điểm của NP và CD là F. Vậy F là điểm chung thứ hai của hai mặt phẳng (MNP) và (BCD).

Vậy giao tuyến của hai mặt phẳng (MNP) và (BCD) là đường thẳng EF.

Bài 4.4 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi P là một điểm thuộc cạnh BC sao cho PC = 2PB.

a) Xác định giao điểm của đường thẳng BD và mặt phẳng (MNP).

b) Xác định giao điểm của đường thẳng AC và mặt phẳng (MNP).

c) Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP).

Lời giải:

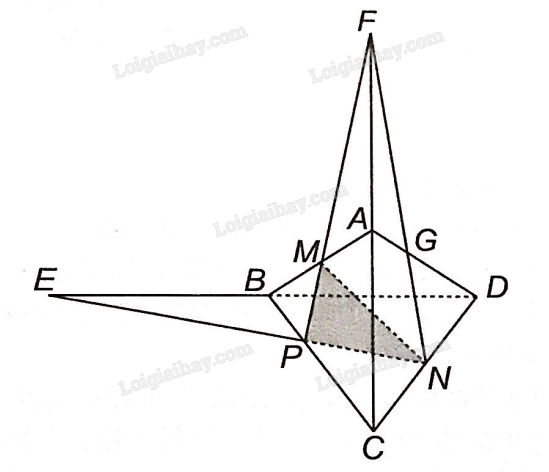
a) Trong mặt phẳng (BCD): Gọi E là giao điểm của BD và PN.

Vậy giao điểm của đường thẳng BD và mặt phẳng (MNP) là điểm E.

b) Trong mặt phẳng (ABC): gọi F là giao điểm của AC và MP.

Vậy giao điểm của đường thẳng AC và mặt phẳng (MNP) là điểm F.

c) Trong mặt phẳng (ADC): gọi G là giao điểm của AD và NF.

Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) là điểm G.

Bài 4.5 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi O là một điểm nằm trong tam giác SCD.

a) Xác định giao tuyến của hai mặt phẳng (SBO) và (SAC).

b) Xác định giao điểm của đường thẳng BO và mặt phẳng (SAC).

Lời giải:

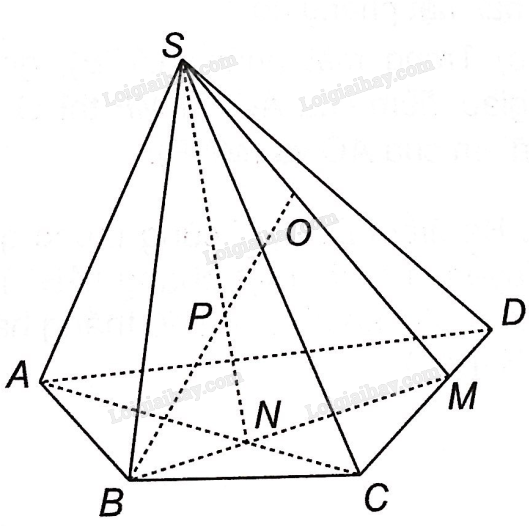
a) Ta thấy S là điểm chung đầu tiên của hai mặt phẳng (SBO) và (SAC).

Trong mặt phẳng (SCD): gọi M là điểm SO giao CD.

Trong mặt phẳng (ABCD): gọi N là giao điểm của BM và AC. Vậy N là điểm chung thứ hai của mặt phẳng (SAC) và (SBM) (trùng với mặt phẳng (SBO)).

Vậy giao tuyến của hai mặt phẳng (SBO) và (SAC) là SN.

b) Trong mặt phẳng (SAC): gọi P là giao điểm của đường thẳng SN và BO.

Vậy giao điểm của đường thẳng BO và mặt phẳng (SAC) là P.

Bài 4.6 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc cạnh AB, AC sao cho $\mathrm{A}\mathrm{E}=\frac{1}{2}\mathrm{B}\mathrm{E}$ và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.

a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).

b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).

Lời giải:

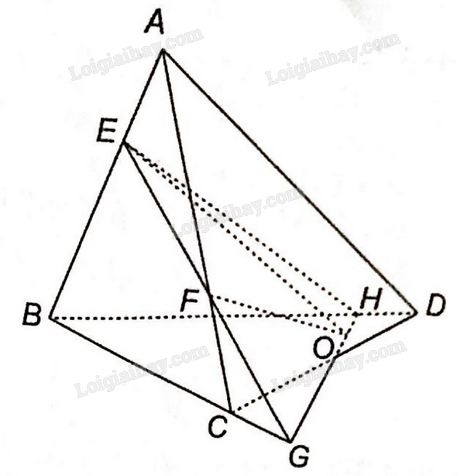
a) Ta thấy E thuộc AB, nằm trong mặt phẳng (ABD). Vậy E là điểm chung thứ nhất của hai mặt phẳng (ABD) và (OEF).

Trong mặt phẳng (ABC) gọi G là giao điểm của EF và BC.

Trong mặt phẳng (BCD), gọi H là giao điểm của BD và OG. Vậy H là một điểm chung của hai mặt phẳng (OEF) và (ABD)

Vậy EH là giao tuyến của hai mặt phẳng (OEF) và (ABD).

b) Trong mặt phẳng (ABD): Gọi I là giao điểm của EH và AD. Vậy I là giao điểm của AD và mặt phẳng (OEF).

SBT Toán 11 trang 56 Tập 1 (Kết nối tri thức)

Bài 4.7 trang 56 SBT Toán 11 Tập 1: Cho tứ diện ABCD và các điểm M, N, P lần lượt thuộc các cạnh AB, AC, AD. Gọi O là một điểm nằm trong tam giác BCD.

a) Xác định giao tuyến của hai mặt phẳng (ABO) và (ACD).

b) Xác định giao tuyến của hai mặt phẳng (ABO) và (MNP).

c) Xác định giao điểm của đường thẳng AO và mặt phẳng (MNP).

Lời giải:

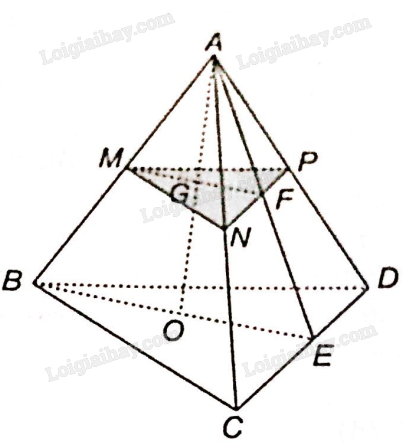
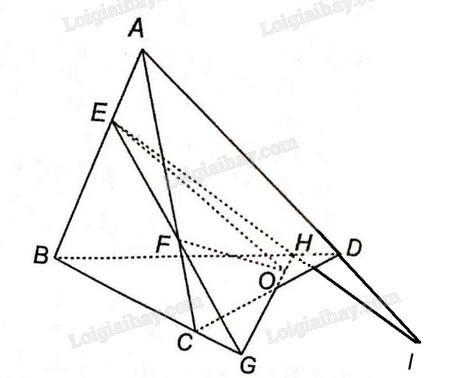
a) Ta thấy A là điểm chung đầu tiên của hai mặt phẳng (ABO) và (ACD).

Trong mặt phẳng (BCD): Gọi E là giao điểm của BO và CD. Vậy E là điểm chung thứ hai của hai mặt phẳng (ABO) và (ACD).

Vậy giao tuyến của hai mặt phẳng (ABO) và (ACD) là đường thẳng AE.

b) Ta thấy M thuộc AB, nằm trong mặt phẳng (ABO) vậy M là điểm chung thứ nhất của hai mặt phẳng (ABO) và (MNP).

Trong mặt phẳng (BCD): gọi E là giao điểm của BO và CD.

Trong mặt phẳng (ACD): gọi F là giao điểm của NP và AE. Vậy F là điểm chung thứ hai của (MNP) và (ABO).

Vậy giao tuyến của hai mặt phẳng (ABO) và (MNP) là đường thẳng MF.

c) Trong mặt phẳng (ABE) gọi G là giao điểm của AO và MF.

Vậy giao điểm của đường thẳng AO và mặt phẳng (MNP) là điểm G.

Bài 4.8 trang 56 SBT Toán 11 Tập 1: Cho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’ và BC cắt nhau tại D, hai đường thẳng C’A’ và CA cắt nhau tại E và hai đường thẳng A’B’ và AB cắt nhau tại F. Chứng minh rằng ba điểm D, E, F thẳng hàng.

Lời giải:

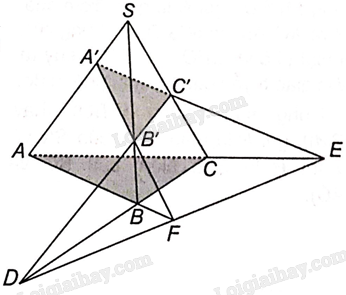
B’C’ và BC cắt nhau tại D nên D nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

C’A’ và CA cắt nhau tại E nên E nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

A’B’ và AB cắt nhau tại F nên F nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

Vậy D, E, F cùng nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC) nên ba điểm này thẳng hàng.

Bài 4.9 trang 56 SBT Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d và một điểm O nằm ngoài cả hai mặt phẳng đó. Gọi A, B là hai điểm phân biệt thuộc mặt phẳng (P) sao cho AB cắt d tại C. Gọi D, E lần lượt là giao điểm của hai đường thẳng OA, OB và mặt phẳng (Q). Chứng minh rằng ba điểm C, D, E thẳng hàng.

Lời giải:

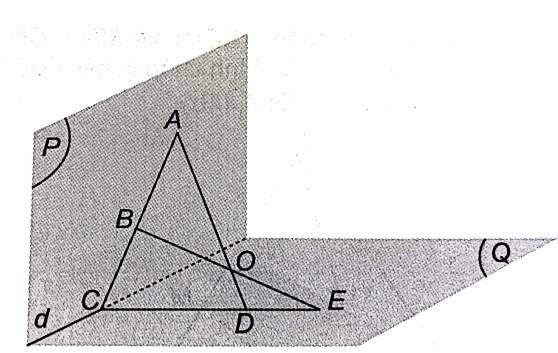
C thuộc AB nằm trong mặt phẳng (ABO), C lại nằm trên giao tuyến của (Q) và (P) nên C là điểm chung của mặt phẳng (ABO) và (Q). C nằm trên giao tuyến của (ABO) và (Q).

D là giao điểm của hai đường thẳng OA và mặt phẳng (Q) nên D nằm trên giao tuyến của (ABO) và (Q).

E là giao điểm của hai đường thẳng OB và mặt phẳng (Q) nên D nằm trên giao tuyến của (ABO) và (Q).

Vậy C, D, E cùng thuộc giao tuyến của hai mặt phẳng (ABO) và (Q) nên chúng thẳng hàng.

Bài 4.10 trang 56 SBT Toán 11 Tập 1: Đánh dấu một điểm trên mép của tờ giấy A4 và dùng kéo cắt một đường bất kì đi qua điểm đó (trong khi cắt không xoay kéo). Hãy giải thích vì sao đường cắt nhận được trên tờ giấy luôn là đường thẳng.

Lời giải:

Đường cắt là giao tuyến của mặt phẳng giấy và mặt phẳng lưỡi kéo, vậy nên đường cắt nhận được luôn là đường thẳng nếu không xoay kéo.

Bài 4.11 trang 56 SBT Toán 11 Tập 1: Bạn Huy đổ nước màu vào một chiếc bể cá có các mặt đều làm bằng kính phẳng. Sau một vài hôm nước bay hơi một phần và để lại trên thành bể cá các vệt màu như trong hình. Huy quan sát thấy rằng, dù bể cá có hình như thế nào, miễn là các mặt đều phẳng thì vệt màu trên mỗi thành bể đều là các đường thẳng. Hãy giải thích vì sao. 

Lời giải:

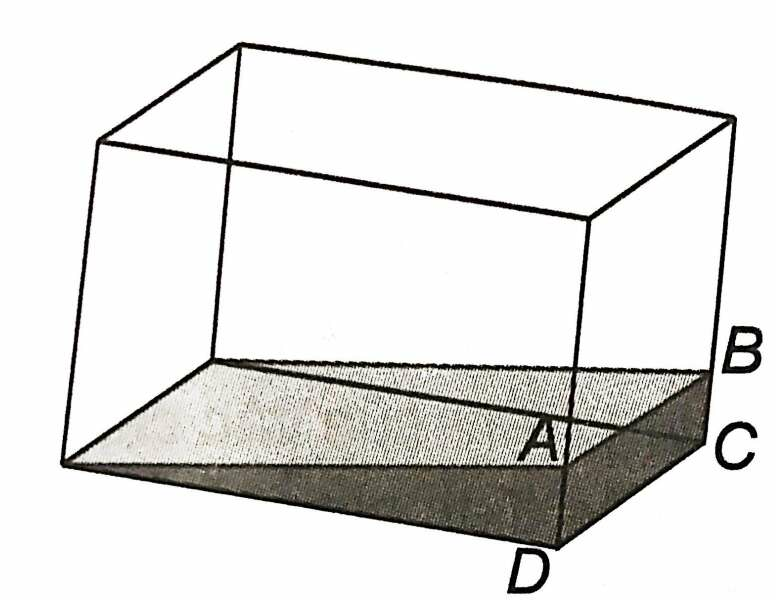
Các vệt màu trên mỗi thành bể đều là giao tuyến của mặt nước và mặt bể vậy nên chúng là các đường thẳng.

Bài 4.12 trang 56 SBT Toán 11 Tập 1: Một số chiếc bàn có thiết kế khung sắt là hai hình chữ nhật có thể xoay quanh một trục, mặt bàn là một tấm gỗ phẳng được đặt lên phần khung như trong hình 4.6. Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt? (Giả sử khung sắt chắc chắn và được đặt cân đối).

Lời giải:

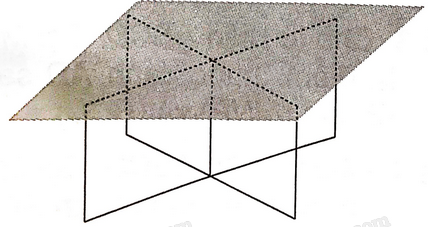
Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt là: Một mặt phẳng được xác định khi nó chứa hai đường thẳng cắt nhau.

Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 3 trang 50

Bài 11: Hai đường thẳng song song

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song