Với Giải trang 56 SBT Toán lớp 11 trong Bài 10: Đường thẳng và mặt phẳng trong không gian Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.

 SBT Toán 11 trang 56 Tập 1 (Kết nối tri thức)

Bài 4.7 trang 56 SBT Toán 11 Tập 1: Cho tứ diện ABCD và các điểm M, N, P lần lượt thuộc các cạnh AB, AC, AD. Gọi O là một điểm nằm trong tam giác BCD.

a) Xác định giao tuyến của hai mặt phẳng (ABO) và (ACD).

b) Xác định giao tuyến của hai mặt phẳng (ABO) và (MNP).

c) Xác định giao điểm của đường thẳng AO và mặt phẳng (MNP).

Lời giải:

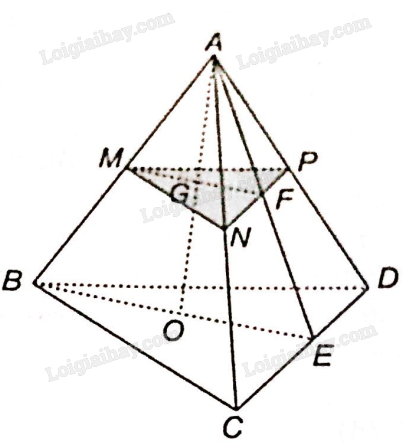
a) Ta thấy A là điểm chung đầu tiên của hai mặt phẳng (ABO) và (ACD).

Trong mặt phẳng (BCD): Gọi E là giao điểm của BO và CD. Vậy E là điểm chung thứ hai của hai mặt phẳng (ABO) và (ACD).

Vậy giao tuyến của hai mặt phẳng (ABO) và (ACD) là đường thẳng AE.

b) Ta thấy M thuộc AB, nằm trong mặt phẳng (ABO) vậy M là điểm chung thứ nhất của hai mặt phẳng (ABO) và (MNP).

Trong mặt phẳng (BCD): gọi E là giao điểm của BO và CD.

Trong mặt phẳng (ACD): gọi F là giao điểm của NP và AE. Vậy F là điểm chung thứ hai của (MNP) và (ABO).

Vậy giao tuyến của hai mặt phẳng (ABO) và (MNP) là đường thẳng MF.

c) Trong mặt phẳng (ABE) gọi G là giao điểm của AO và MF.

Vậy giao điểm của đường thẳng AO và mặt phẳng (MNP) là điểm G.

Bài 4.8 trang 56 SBT Toán 11 Tập 1: Cho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’ và BC cắt nhau tại D, hai đường thẳng C’A’ và CA cắt nhau tại E và hai đường thẳng A’B’ và AB cắt nhau tại F. Chứng minh rằng ba điểm D, E, F thẳng hàng.

Lời giải:

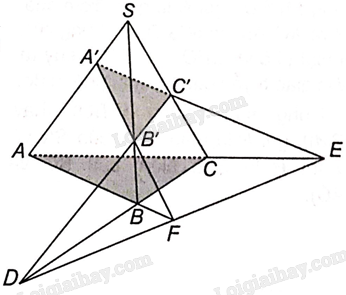
B’C’ và BC cắt nhau tại D nên D nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

C’A’ và CA cắt nhau tại E nên E nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

A’B’ và AB cắt nhau tại F nên F nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

Vậy D, E, F cùng nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC) nên ba điểm này thẳng hàng.

Bài 4.9 trang 56 SBT Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d và một điểm O nằm ngoài cả hai mặt phẳng đó. Gọi A, B là hai điểm phân biệt thuộc mặt phẳng (P) sao cho AB cắt d tại C. Gọi D, E lần lượt là giao điểm của hai đường thẳng OA, OB và mặt phẳng (Q). Chứng minh rằng ba điểm C, D, E thẳng hàng.

Lời giải:

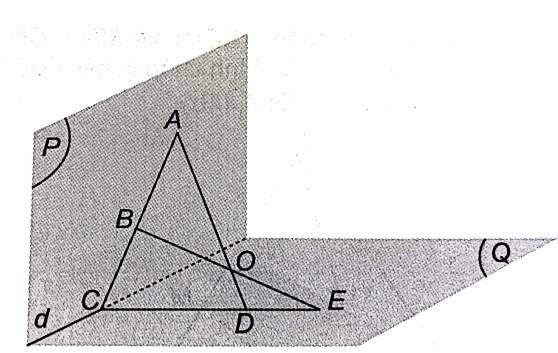
C thuộc AB nằm trong mặt phẳng (ABO), C lại nằm trên giao tuyến của (Q) và (P) nên C là điểm chung của mặt phẳng (ABO) và (Q). C nằm trên giao tuyến của (ABO) và (Q).

D là giao điểm của hai đường thẳng OA và mặt phẳng (Q) nên D nằm trên giao tuyến của (ABO) và (Q).

E là giao điểm của hai đường thẳng OB và mặt phẳng (Q) nên D nằm trên giao tuyến của (ABO) và (Q).

Vậy C, D, E cùng thuộc giao tuyến của hai mặt phẳng (ABO) và (Q) nên chúng thẳng hàng.

Bài 4.10 trang 56 SBT Toán 11 Tập 1: Đánh dấu một điểm trên mép của tờ giấy A4 và dùng kéo cắt một đường bất kì đi qua điểm đó (trong khi cắt không xoay kéo). Hãy giải thích vì sao đường cắt nhận được trên tờ giấy luôn là đường thẳng.

Lời giải:

Đường cắt là giao tuyến của mặt phẳng giấy và mặt phẳng lưỡi kéo, vậy nên đường cắt nhận được luôn là đường thẳng nếu không xoay kéo.

Bài 4.11 trang 56 SBT Toán 11 Tập 1: Bạn Huy đổ nước màu vào một chiếc bể cá có các mặt đều làm bằng kính phẳng. Sau một vài hôm nước bay hơi một phần và để lại trên thành bể cá các vệt màu như trong hình. Huy quan sát thấy rằng, dù bể cá có hình như thế nào, miễn là các mặt đều phẳng thì vệt màu trên mỗi thành bể đều là các đường thẳng. Hãy giải thích vì sao. 

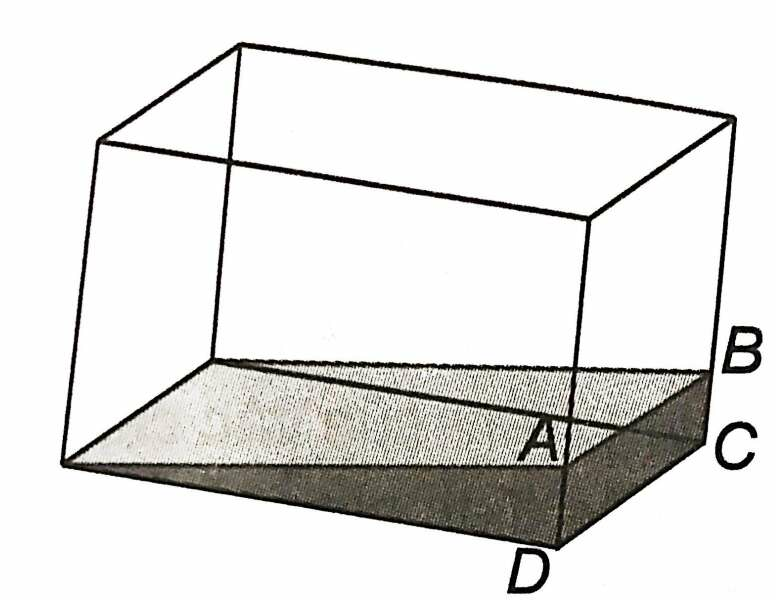
Lời giải:

Các vệt màu trên mỗi thành bể đều là giao tuyến của mặt nước và mặt bể vậy nên chúng là các đường thẳng.

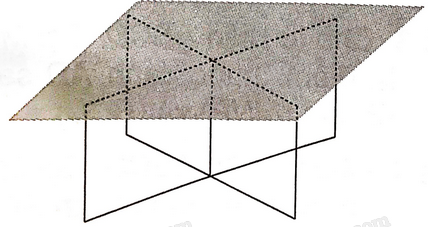
Bài 4.12 trang 56 SBT Toán 11 Tập 1: Một số chiếc bàn có thiết kế khung sắt là hai hình chữ nhật có thể xoay quanh một trục, mặt bàn là một tấm gỗ phẳng được đặt lên phần khung như trong hình 4.6. Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt? (Giả sử khung sắt chắc chắn và được đặt cân đối).

Lời giải:

Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt là: Một mặt phẳng được xác định khi nó chứa hai đường thẳng cắt nhau.