Với Giải trang 68 SBT Toán lớp 11 trong Bài 13: Hai mặt phẳng song song Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.

 SBT Toán 11 trang 68 Tập 1 (Kết nối tri thức)

Bài 4.33 trang 68 SBT Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng sau điểm A, B, C, D, E, F là sáu đỉnh của một hình lăng trụ tam giác.

Lời giải:

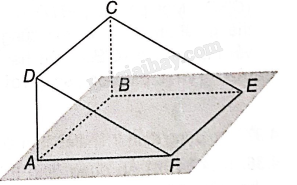
Vì AD//BC (do ABCD là hình bình hành) nên AD//mp (BCE), AF//BE (do ABEF là hình bình hành) nên AF//mp (BCE).

Mà AD và AF là hai đường thẳng cắt nhau cùng nằm trong mặt phẳng ADF. Do đó, mp (ADF) //mp (BCE).

Các đường thẳng AB, CD, EF đôi một song song với nhau.

Bài 4.34 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng (P) cắt các cạnh AD, BC, B’C’, A’D’ lần lượt tại E, F, G, H. Chứng minh rằng tứ giác EFGH là hình bình hành.

Lời giải:

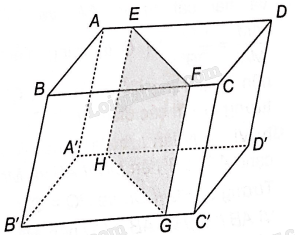
Vì hai mặt phẳng (ABCD) và (A’B’C’D’) của hình hộp song song với nhau nên giao tuyến của mặt phẳng (EFGH) và hai mặt phẳng đó song song với nhau, tức là EF//GH

Vì hai mặt phẳng (AA’D’D) và (B’B’C’B) của hình hộp song song với nhau nên giao tuyến của mặt phẳng (EFGH) và hai mặt phẳng đó song song với nhau, tức là EH//GF

Tứ giác EFGH có: EF//GH, EH//GF nên tứ giác EFGH là hình bình hành.

Bài 4.35 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’.

a) Xác định giao tuyến d của hai mặt phẳng (ADC’B’) và (A’D’CB).

b) Chứng minh rằng d // AD.

c) Chứng minh rằng d đi qua trung điểm của các đường chéo của hình hộp.

Lời giải:

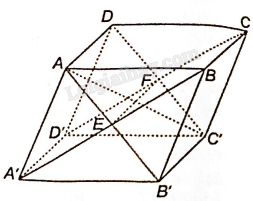
 a) Gọi E là giao điểm của AB’ và A’B; gọi F là giao điểm của CD’ và C’D. Vì đường thẳng EF vừa thuộc cả hai mặt phẳng (ADC’B’) và (A’D’CB) nên EF là giao tuyến của hai mặt phẳng (ADC’B’) và (A’D’CB).

b) Hai mặt phẳng (ADC’B’) và (A’D’CB) chứa hai đường thẳng song song là AD và BC nên giao tuyến EF của hai mặt phẳng đó song song với AD.

c) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, $AD=BC$ và BC//B’C’ và $BC=B^{\prime }{C}^{\prime }$, do đó ADC’B’ là hình bình hành.

Vì E, F lần lượt là trung điểm của AB’ và CD’ nên EF đi qua trung điểm của AC’. Vì các đường chéo của hình hộp cùng đi qua trung điểm của mỗi đường nên đường thẳng EF đi qua trung điểm các đường chéo đó.

Bài 4.36 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:

a) AB’//C’D’;      

b) Hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.

Lời giải:

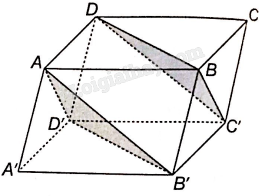
a) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, $AD=BC$ và BC//B’C’ và $BC=B^{\prime }{C}^{\prime }$, do đó ADC’B’ là hình bình hành nên AB’//C’D.

b) Vì AB’//C’D nên AB’//mp(C’BD)

Chứng minh tương tự ta có: AD’//BC’ nên AD’//mp(C’BD). Mặt phẳng (AB’D’) có hai đường thẳng cắt nhau AB’ và AD’ cùng song song với mp(C’BD) nên hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.

Bài 4.37 trang 68 SBT Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’. Biết rằng AB = 2cm, BC = 6cm và A’B’ = 3cm, tính B’C’.

Lời giải:

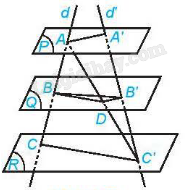
Vì ba mặt phẳng (P), (Q), (R) đôi một song song và hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ nên $\frac{AB}{BC}=\frac{A^{\prime }{B}^{\prime }}{B^{\prime }{C}^{\prime }}$ (định lí Thalès)$\Rightarrow \frac{2}{6}=\frac{3}{B^{\prime }{C}^{\prime }}\Rightarrow B^{\prime }{C}^{\prime }=\frac{3.6}{2}=9\left(cm\right)$

Bài 4.38 trang 68 SBT Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng (ABCD) cắt các cạnh AA’, BB’, CC’, DD’ lần lượt tại M, N, P, Q.

a) Chứng minh rằng M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’.

b) Chứng minh rằng ABCD.MNPQ là hình hộp.

Lời giải:

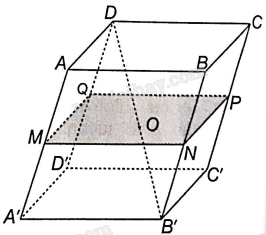
a) Áp dụng định lí Thalès cho ba mặt phẳng (ABCD), (MNPQ), (A’B’C’D’) và hai cát tuyến AA’, DB’ ta có: $\frac{AM}{M{A}^{\prime }}=\frac{DO}{O{B}^{\prime }}$

Vì O là trung điểm của DB’ nên M là trung điểm của AA’.

Chứng minh tương tự ta có: N, P, Q lần lượt là trung điểm của BB’, CC’, DD’.

b) Vì M, N lần lượt là trung điểm của AA’, BB’ nên MN//AB, $MN=AB$

Tương tự ta có: PQ//CD và $PQ=CD$

Vì $AB=CD$ và AB//CD nên $MN=PQ$ và MN//PQ.

Do đó tứ giác MNPQ là hình bình hành.

Vì các đường thẳng AM, BN, CP, DQ đôi một song song nên suy ra ABCD.MNPQ là hình hộp.

Bài 4.39 trang 68 SBT Toán 11 Tập 1: Khi cắt một chiếc bánh gato hình hộp, Thúy nhận thấy vết cắt ở mặt trên và mặt dưới của bánh gợi nên hình ảnh về hai đường thẳng song song với nhau. Hỏi nhận xét của Thúy có đúng không? Vì sao?

Lời giải:

Khi Thúy cắt bánh thì lưỡi dao di chuyển tạo thành một mặt phẳng cắt hai mặt trên và dưới của chiếc bánh. Vì mặt trên và mặt dưới của chiếc bánh song song với nhau nên các vết cắt (chính là giao tuyến của mặt phẳng cắt và hai mặt bánh) song song với nhau.

Bài 4.40 trang 68 SBT Toán 11 Tập 1: Một chiếc bình nước hình trụ được đặt trên bàn, lượng nước trong bình bằng đúng một nửa dung tích của bình. Hoàng đặt một chiếc ống hút vào trong bình sao cho cho một đầu của ống hút chạm vào đáy bình còn một đầu chạm vào miệng bình. Hoàng nói rằng độ dài của phần ống hút bị ướt bằng độ dài của toàn bộ ống hút. Hỏi Hoàng nói đúng hay sai? Vì sao?

Lời giải:

Hoàng nói sai, theo định lí Thalès trong không gian thì độ dài của phần ống bị ướt bằng $\frac{1}{2}$ độ dài của toàn bộ ống hút