Lý thuyết Thứ tự thực hiện các phép tính. Quy tắc chuyển vế (Kết nối tri thức) Toán 7

Giang Ngày: 08-03-2024 Lớp 7

Tải xuống 11 330 4

Toptailieu.vn biên soạn và giới thiệu Lý thuyết Thứ tự thực hiện các phép tính. Quy tắc chuyển vế (Kết nối tri thức) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.

Lý thuyết Thứ tự thực hiện các phép tính. Quy tắc chuyển vế (Kết nối tri thức) Toán 7

A. Lý thuyết

1. Thứ tự thực hiện các phép tính

• Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia ta thực hiện các phép tính theo thứ tự từ trái sang phải.

• Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:

Thứ tự thực hiện các phép tính. Quy tắc chuyển vế (Lý thuyết + Bài tập toán lớp 7) – Kết nối tri thức (ảnh 1)

• Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.

$() \to [] \to \{\}$

Ví dụ: Tính giá trị của biểu thức:

a) 1,5 – 2³ + 7,5 : 3;

b) $\frac{3}{2} : (\frac{1}{11} - \frac{5}{22}) + \frac{7}{4} \cdot (\frac{1}{14} - \frac{2}{7})$ .

Hướng dẫn giải:

a) 1,5 – 2³ + 7,5 : 3

= 1,5 – 8 + 2,5 (Thực hiện lũy thừa; nhân chia trước)

= – 6,5 + 2,5 = – 4

b) $\frac{3}{2} : (\frac{1}{11} - \frac{5}{22}) + \frac{7}{4} \cdot (\frac{1}{14} - \frac{2}{7})$

$= \frac{3}{2} : (- \frac{3}{22}) + \frac{7}{4} \cdot (- \frac{3}{14})$ (Thực hiện trong ngoặc trước)

$= \frac{3}{2} \cdot (- \frac{22}{3}) + (- \frac{3}{8})$ (Thực hiện nhân chia trước)

$= (- 11) + (- \frac{3}{8}) = - \frac{91}{8}$ .

2. Quy tắc chuyển vế

• Đẳng thức có dạng A = B. Trong đó A là vế trái; B là vế phải của đẳng thức.

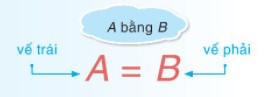
Thứ tự thực hiện các phép tính. Quy tắc chuyển vế (Lý thuyết + Bài tập toán lớp 7) – Kết nối tri thức (ảnh 1)

Ví dụ: 4,1 + x = 2,3 là một đẳng thức, trong đó 4,1 + x là vế trái, 2,3 là vế phải.

• Khi biến đổi các đẳng thức, ta thường áp dụng các tính chất sau:

Nếu a = b thì: b = a; a + c = b + c.

• Quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu “+”.

+) Nếu a + b = c thì a = c – b;

+) Nếu a – b = c thì a = c + b.

Ví dụ: Tìm x, biết:

a) $x + \frac{1}{3} = - \frac{5}{7}$ ;

b) $x - \frac{5}{4} = \frac{9}{8}$ .

Hướng dẫn giải

a) $x + \frac{1}{3} = - \frac{5}{7}$

$x = - \frac{5}{7} - \frac{1}{3}$ (Quy tắc chuyển vế)

$x = - \frac{15}{21} - \frac{7}{21}$

$x =- \frac{22}{21}$

Vậy $x = - \frac{22}{21}$ .

b) $x - \frac{5}{4} = \frac{9}{8}$

$x = \frac{9}{8} + \frac{5}{4}$ (Quy tắc chuyển vế)

$x = \frac{9}{8} + \frac{10}{8}$

$x = \frac{19}{8}$

Vậy $x = \frac{19}{8}$ .

B. Bài tập tự luyện

B1. Bài tập tự luận

Bài 1. Tính một cách hợp lí.

a) $4, 64 + {(\frac{- 1}{2})}^{3} + 0, 6^{2} - 3 \cdot \frac{- 3}{8}$ ;

b) $2022, 123 \cdot 2023 + 2022, 123 \cdot {(- 2023)}^{2022 - 2021}$ .

Hướng dẫn giải

a) $4, 64 + {(\frac{- 1}{2})}^{3} + 0, 6^{2} - 3 \cdot \frac{- 3}{8}$

$= 4, 64 + \frac{- 1}{8} + 0, 36 - \frac{- 9}{8}$

$= (4, 64 + 0, 36) + (\frac{- 1}{8} - \frac{- 9}{8})$

$= 5 + (\frac{- 1}{8} + \frac{9}{8})$

$= 5 + \frac{8}{8} = 5 + 1 = 6$

b) $2022, 123 \cdot 2023 + 2022, 123 \cdot {(- 2023)}^{2022 - 2021}$

$= 2022, 123 \cdot 2023 + 2022, 123 \cdot (- 2023)$

$= 2022, 123 \cdot [2023 + (- 2023)]$

$= 2022, 123 \cdot 0 = 0$

Bài 2. Tính giá trị của biểu thức sau:

a) $(\frac{2}{3} + \frac{1}{6}) : \frac{5}{4} + (\frac{1}{4} + \frac{3}{8}) : \frac{5}{2}$ ;

b) $2 : {(\frac{1}{2} - \frac{2}{3})}^{2} + 0, 25^{3} \cdot 4^{3} - {(- 12)}^{4} : 6^{4}$ ;

c) $7 \cdot 2^{3} - 5 \cdot \{[10, 51 + 4 \cdot {(\frac{3}{4} - \frac{2}{5})}^{2}] - 2022^{0}\}$ .

Hướng dẫn giải

a) $(\frac{2}{3} + \frac{1}{6}) : \frac{5}{4} + (\frac{1}{4} + \frac{3}{8}) : \frac{5}{2}$

$= (\frac{4}{6} + \frac{1}{6}) \cdot \frac{4}{5} + (\frac{2}{8} + \frac{3}{8}) \cdot \frac{2}{5}$

$= \frac{5}{6} \cdot \frac{4}{5} + \frac{5}{8} \cdot \frac{2}{5}$

$= \frac{2}{3} + \frac{1}{4}$

$= \frac{8}{12} + \frac{3}{12}$

$= \frac{11}{12}$

b) $2 : {(\frac{1}{2} - \frac{2}{3})}^{2} + 0, 25^{3} \cdot 4^{3} - {(- 12)}^{4} : 6^{4}$

$= 2 : {(- \frac{1}{6})}^{2} + {(\frac{1}{4})}^{3} \cdot 4^{3} - {(- 2 \cdot 6)}^{4} : 6^{4}$

$= 2 : \frac{1}{36} + \frac{1^{3}}{4^{3}} \cdot 4^{3} - {(- 2)}^{4} \cdot {(6)}^{4} : 6^{4}$

$= 2 \cdot 36 + 1 - {(- 2)}^{4}$

$= 72 + 1 - 16 = 57$

c) $7 \cdot 2^{3} - 5 \cdot \{[10, 51 + 4 \cdot {(\frac{3}{4} - \frac{2}{5})}^{2}] - 2022^{0}\}$

$= 7 \cdot 8 - 5 \cdot \{[10, 51 + 4 \cdot {(\frac{7}{20})}^{2}] - 1\}$

$= 56 - 5 \cdot \{[10, 51 + 4 \cdot \frac{49}{400}] - 1\}$

$= 56 - 5 \cdot \{[10, 51 + \frac{49}{100}] - 1\}$

$= 56 - 5 \cdot \{[10, 51 + 0, 49] - 1\}$

$= 56 - 5 \cdot \{11 - 1\}$

$= 56 - 5 \cdot 10 = 6$

Bài 3. Tìm x, biết:

a) $x + 0, 5 = - \frac{2}{3}$ ;

b) $x - (- \frac{2}{5}) = \frac{5}{7}$ ;

c) $\frac{5}{4} - 6 x = \frac{7}{12}$ ;

d) $3 - 2 x - (\frac{5}{4} - \frac{7}{5}) = \frac{9}{20}$ .

Hướng dẫn giải

a) $x + 0, 5 = - \frac{2}{3}$

$x = - \frac{2}{3} - 0, 5$

$x = - \frac{2}{3} - \frac{1}{2}$

$x = - \frac{4}{6} - \frac{3}{6}$

$x = - \frac{7}{6}$

Vậy $x = - \frac{7}{6}$

b) $x - (- \frac{2}{5}) = \frac{5}{7}$

$x = \frac{5}{7} + (- \frac{2}{5})$

$x= \frac{5}{7} - \frac{2}{5}$

$x = \frac{25}{35} - \frac{14}{35}$

$x = \frac{11}{35}$

Vậy $x = \frac{11}{35}$

c) $\frac{5}{4} - 6 x = \frac{7}{12}$

$- 6 x = \frac{7}{12} - \frac{5}{4}$

$- 6 x = \frac{7}{12} - \frac{15}{12}$

$- 6 x = \frac{- 8}{12}$

$x = \frac{- 8}{12} : (- 6)$

$x = \frac{- 8}{12} \cdot \frac{- 1}{6}$

$x = \frac{1}{9}$

Vậy $x = \frac{1}{9}$

d) $3 - 2 x - (\frac{5}{4} - \frac{7}{5}) = \frac{9}{20}$

$3 - 2 x - (\frac{- 3}{20}) = \frac{9}{20}$

$- 2 x = \frac{9}{20} + (\frac{- 3}{20}) - 3$

$- 2 x = \frac{6}{20} - 3$

$- 2 x = \frac{3}{10} - \frac{30}{10}$

$- 2 x = \frac{- 27}{10}$

$x = \frac{- 27}{10} : (- 2)$

$x = \frac{27}{20}$

Vậy $x = \frac{27}{20}$

B2. Bài tập trắc nghiệm

Bài 4. Tính $7 \cdot 2^{3} - 5 \{[10, 51 + 4 \cdot {(\frac{3}{4} - \frac{2}{5})}^{2}] - 2021^{0}\}$

A. 6;

B. 2021;

C. 56;

D. 51.

Hướng dẫn giải

Đáp án đúng là: A

$7 \cdot 2^{3} - 5 \{[10, 51 + 4 \cdot {(\frac{3}{4} - \frac{2}{5})}^{2}] - 2021^{0}\}$

$= 7 \cdot 8 - 5 \{[10, 51 + 4 \cdot {(\frac{7}{20})}^{2}] - 1\}$

$= 56 - 5 \{[10, 51 + 4 \cdot \frac{49}{400}] - 1\}$

$= 56 - 5 \{[10, 51 + \frac{49}{100}] - 1\}$

$= 56 - 5 \{[10, 51 + 0, 49] - 1\}$

$= 56 - 5 \{11 - 1\}$

$= 56 - 5 \cdot 10 = 6$

Bài 5. Tìm x, biết: $3 - 3 x - (\frac{5}{4} - \frac{7}{5}) = \frac{9}{20}$

A. $x = \frac{9}{10}$ ;

B. $x = \frac{- 9}{10}$ ;

C. $x = \frac{10}{9}$ ;

D. $x = \frac{- 10}{9}$ .

Hướng dẫn giải

Đáp án đúng là: A

$3 - 3 x - (\frac{5}{4} - \frac{7}{5}) = \frac{9}{20}$

$3 - 3 x - (\frac{- 3}{20}) = \frac{9}{20}$

$- 3 x = \frac{9}{20} + (\frac{- 3}{20}) - 3$

$- 3 x = \frac{6}{20} - 3$

$- 3 x = \frac{3}{10} - \frac{30}{10}$

$- 3 x = \frac{- 27}{10}$

$x = \frac{- 27}{10} : (- 3)$

$x = \frac{9}{10}$ . Vậy $x = \frac{9}{10}$

Bài 6. Một ô tô đã đi 110 km trong 3 giờ. Trong giờ thứ nhất, xe đi được $\frac{1}{3}$ quãng đường. Trong giờ thứ hai, xe đi được $\frac{2}{5}$ quãng đường còn lại. Hỏi trong giờ thứ ba xe đi được bao nhiêu ki-lô-mét?

A. 45 km;

B. 44 km;

C. 47 km;

D. 46 km.

Hướng dẫn giải

Đáp án đúng là: B

Giờ thứ nhất đi được số ki-lô-mét là: $110 \cdot \frac{1}{3}$ = $\frac{110}{3}$ (km)

Giờ thứ hai đi được số ki-lô-mét là: $(110 - \frac{110}{3}) \cdot \frac{2}{5}$ = $\frac{88}{3}$ (km)

Giờ thứ ba xe đi được số ki-lô-mét là: $110 - (\frac{110}{3} + \frac{88}{3})$ = 44 (km)

Tài liệu có 11 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Giải bài tập Toán 7

Đánh giá

0 đánh giá

Đánh giá

Tài liệu cùng môn học

Toán Lớp 7 pdf

Lý thuyết Ôn tập chương 7 (Cánh Diều) Toán 7 Giang Tiêu đề (copy ở trên xuống) - Trọn bộ lý thuyết Toán 7 Cánh Diều hay, chi tiết giúp em học tốt Toán 7.

680 47 14

Toán Lớp 7 pdf

Lý thuyết Tính chất ba đường cao của tam giác (Cánh Diều) Toán 7 Giang Lý thuyết Tính chất ba đường cao của tam giác (Cánh Diều) Toán 7 - Trọn bộ lý thuyết Toán 7 Cánh Diều hay, chi tiết giúp em học tốt Toán 7.

582 12 6

Toán Lớp 7 pdf

Lý thuyết Tính chất ba đường trung trực của tam giác (Cánh Diều) Toán 7 Giang Lý thuyết Tính chất ba đường trung trực của tam giác (Cánh Diều) Toán 7 - Trọn bộ lý thuyết Toán 7 Cánh Diều hay, chi tiết giúp em học tốt Toán 7.

659 12 9

Toán Lớp 7 pdf

Lý thuyết Tính chất ba đường phân giác của tam giác (Cánh Diều) Toán 7 Giang Lý thuyết Tính chất ba đường phân giác của tam giác (Cánh Diều) Toán 7 - Trọn bộ lý thuyết Toán 7 Cánh Diều hay, chi tiết giúp em học tốt Toán 7.

648 13 8